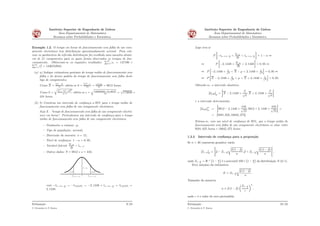
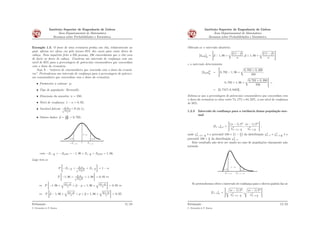
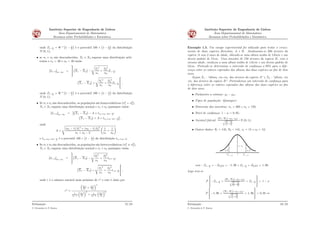
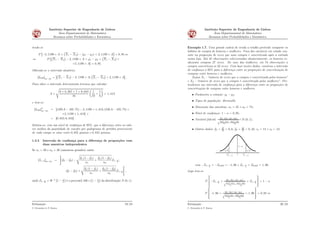
1) O documento discute estimação estatística, que envolve usar dados amostrais para fazer inferências sobre parâmetros populacionais. 2) Existem dois métodos para determinar estimadores de parâmetros: o método dos momentos e o método da máxima verossimilhança. 3) Um intervalo de confiança é um intervalo que tem probabilidade especificada de conter o verdadeiro valor do parâmetro, e é usado para estimar parâmetros com mais precisão do que um único valor pontual.