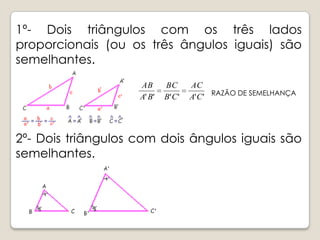
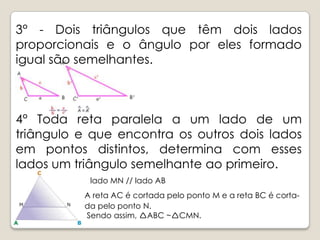
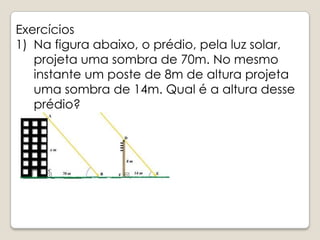
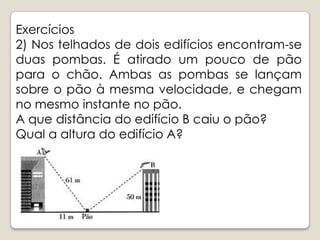
A lenda conta que Tales mediu a altura da Grande Pirâmide de Gizé usando semelhança de triângulos. O documento explica o conceito de homotetia e como ela estabelece a semelhança entre figuras geométricas. São apresentados critérios para determinar se dois triângulos são semelhantes e exercícios sobre semelhança de triângulos são propostos.

1. OBJETO DE APRENDIZAGEMCURSO DE PÓS-GRADUAÇÃOUNIVERSIDADE FEDERAL FLUMINENSEINFORMÁTICA EDUCATIVA 2Maria Fernanda Bastos OliveiraPólo Campinas

2. Conta a lenda que quando o matemático e filósofo grego Tales (século VI a.C.) chegou ao Egito, os sacerdotes pediram-lhe que averiguasse a altura da pirâmide de Quéops.

3. Tales traçou uma linha no solo, marcando nela sua altura e esperou que sua sombra, projetada pelo sol, ficasse igual à sua altura; nesse momento, mediu a sombra projetada pela pirâmide. O matemático respondeu aos sacerdotes: "Agora que minha sombra é igual à minha altura, o comprimento da sombra da pirâmide deve coincidir com o comprimento de sua altura".

4. Antes de iniciarmos o estudo de semelhança de triângulos, é importante estudarmos a transformação de figuras através da HOMOTETIA.Homotetia é a ampliação ou redução das figuras geométricas.Um movimento composto com uma homotetia, estabelece uma correspondência biunívoca entre os pontos da figura. Essa correspondência, ou seja,

5. essa transformação assim considerada é chamada semelhança.Podemos então concluir que, se dois polígonos são semelhantes, então:Os ângulos correspondentes são congruentes

6. A razão entre as medidas dos lados correspondentes é constante e igual à razão de semelhança.Veja a matemática da Homotetia:

7. Podemos compreender melhor este conceito, aplicando-o a figuras geométricas bem simples: TRIÂNGULOS! SEMELHANÇA DE TRIÂNGULOSDois triângulos dizem-se semelhantes quando têm os ângulos respectivamente iguais e os lados homólogos proporcionais. Porém, para se afirmar que dois triângulos são semelhantes, basta que se verifiquem apenas algumas condições ou Critérios de Semelhança de Triângulos:

8. 1º- Dois triângulos com os três lados proporcionais (ou os três ângulos iguais) são semelhantes.RAZÃO DE SEMELHANÇA2º- Dois triângulos com dois ângulos iguais são semelhantes.

9. 3° - Dois triângulos que têm dois lados proporcionais e o ângulo por eles formado igual são semelhantes.4° Toda reta paralela a um lado de um triângulo e que encontra os outros dois lados em pontos distintos, determina com esses lados um triângulo semelhante ao primeiro. lado MN // lado ABA reta AC é cortada pelo ponto M e a reta BC é corta- da pelo ponto N. Sendo assim, ABC ~CMN.

11. ExercíciosNa figura abaixo, o prédio, pela luz solar, projeta uma sombra de 70m. No mesmo instante um poste de 8m de altura projeta uma sombra de 14m. Qual é a altura desse prédio?

12. Exercícios2) Nos telhados de dois edifícios encontram-se duas pombas. É atirado um pouco de pão para o chão. Ambas as pombas se lançam sobre o pão à mesma velocidade, e chegam no mesmo instante no pão.A que distância do edifício B caiu o pão?Qual a altura do edifício A?