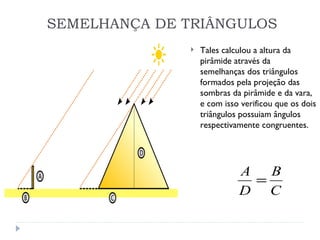
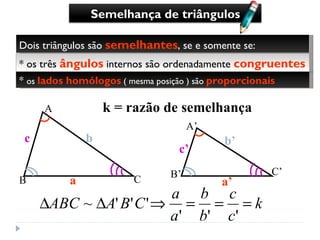
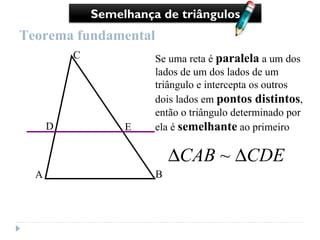
1) Tales de Mileto calculou a altura da Grande Pirâmide de Quéops no século 7 a.C. ao fincar uma vara no solo e observar a proporção entre as sombras; 2) Ele aplicou o conceito de triângulos semelhantes, sabendo que a razão entre a altura e a sombra é sempre a mesma; 3) Tales mediu a altura da pirâmide usando a semelhança dos triângulos formados pelas sombras da vara e da pirâmide.

5. Teorema de Tales Dados: um feixe de retas paralelas e retas transversais, a razão entre as medidas dos segmentos quaisquer de uma das transversais é igual à razão entre as medidas dos segmentos correspondentes de outra. A B A’ B’ C D C’ D’ As medidas dos segmentos correspondentes nas transversais são diretamente proporcionais

6. Teorema da bissetriz interna Uma bissetriz interna de um triângulo divide o lado oposto em segmentos proporcionais aos lados adjacentes c b D Teorema de Tales A B C   x y

7. Teorema da bissetriz interna r r//s Ângulos alternos internos Ângulos correspondentes Teorema de Tales A B C   c b D x y  

8. Teorema de Tales Teorema da bissetriz interna E Logo o triângulo ACE é isósceles  AC = AE = b b Pelo Teorema de Tales temos: A B C   c b D x y r r//s  

9. * os três ângulos internos são ordenadamente congruentes Dois triângulos são semelhantes , se e somente se: * os lados homólogos ( mesma posição ) são proporcionais a a’ b’ b c c’ k = razão de semelhança Semelhança de triângulos A B C A’ B’ C’

10. Teorema fundamental Se uma reta é paralela a um dos lados de um dos lados de um triângulo e intercepta os outros dois lados em pontos distintos , então o triângulo determinado por ela é semelhante ao primeiro Semelhança de triângulos A B C D E

11. Semelhança de triângulos Casos ( ou critérios ) de semelhança 1- dois ângulos ordenadamente congruentes 2- LAL lados proporcionais e ângulos entre eles congruentes 3- LLL lados homólogos proporcionais

13. Componentes: Felipe Samuel Paulo Cezar Alisson Lopes Série/Turma: 3ºC