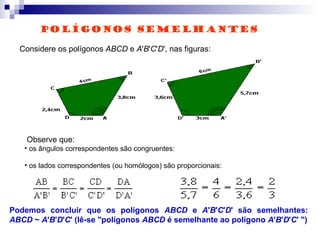
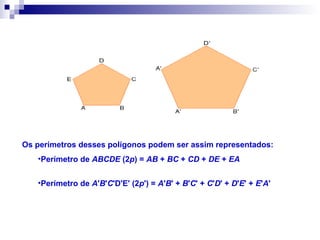
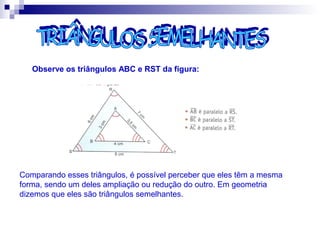
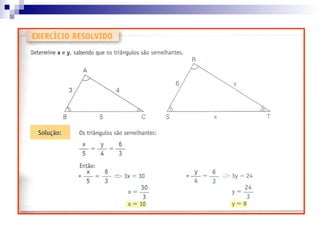
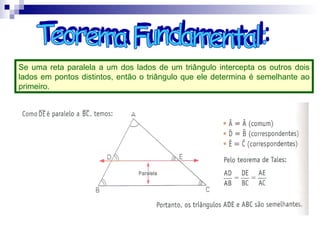
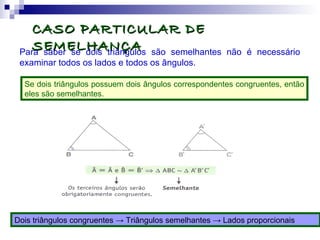
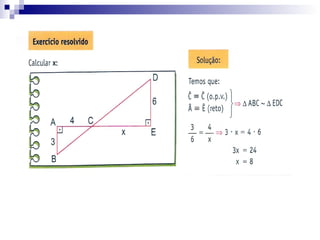
O documento discute semelhança de polígonos e triângulos. Dois polígonos são semelhantes se tiverem ângulos correspondentes congruentes e lados correspondentes proporcionais. Dois triângulos são semelhantes se tiverem dois ângulos correspondentes congruentes. Exemplos e exercícios ilustram como calcular lados e perímetros de figuras semelhantes.

2. QUAL É A ÚNICA DIFERENÇA ENTRE AS IMAGENS
APRESENTADAS?

3. Figuras que apresentam a mesma forma, mas possuem tamanhos
diferentes, são chamadas figuras semelhantes.

4. APLICAÇÕES DAAPLICAÇÕES DA
SEMELHANÇASEMELHANÇA

5. Considere os polígonos ABCD e A'B'C'D', nas figuras:
Observe que:
• os ângulos correspondentes são congruentes:
• os lados correspondentes (ou homólogos) são proporcionais:
Podemos concluir que os polígonos ABCD e A'B'C'D' são semelhantes:
ABCD ~ A'B'D'C' (lê-se "polígonos ABCD é semelhante ao polígono A'B'D'C' ")
POLÍGONOS SEMELHANTES

6. Dois polígonos são semelhantes quando os ângulos
correspondentes são congruentes e os lados correspondentes são
proporcionais.
A razão entre dois lados correspondentes em polígonos semelhante
denomina-se razão de semelhança, ou seja:
Obs: A definição de polígonos semelhantes só é válida quando
ambas as condições são satisfeitas: Ângulos correspondentes
congruentes e lados correspondentes proporcionais. Apenas
uma das condições não é suficiente para indicar a semelhança
entre polígonos.
Se dois polígonos são semelhantes, então a razão entre seus
perímetros é igual à razão entre as medidas de dois lados
homólogos quaisquer dos polígonos.
PROPRIEDADES:PROPRIEDADES:

7. Os perímetros desses polígonos podem ser assim representados:
•Perímetro de ABCDE (2p) = AB + BC + CD + DE + EA
•Perímetro de A'B'C'D'E' (2p') = A'B' + B'C' + C'D' + D'E' + E'A'

8. Exemplo:
Os lados de um triângulo medem 3,6 cm, 6,4 cm e 8 cm. Esse triângulo é semelhante
a um outro cujo perímetro mede 45 cm. calcule os lados do segundo triângulo.
Solução
Logo, os lados do segundo triângulo são 9cm, 16cm e 20cm.

9. Observe os triângulos ABC e RST da figura:
Comparando esses triângulos, é possível perceber que eles têm a mesma
forma, sendo um deles ampliação ou redução do outro. Em geometria
dizemos que eles são triângulos semelhantes.

10. Dois triângulos são semelhantes quando têm:
Os ângulos respectivamente congruentes;
Os lados correspondentes (são os lados opostos ao mesmo ângulo)
proporcionais.
Em relação aos triângulos anteriores, a razão de semelhança do menor
triângulo para o maior é:
semelhançaderazão⇒===
2
1
7
5,3
8
4
6
3
Obs.: Se a razão de semelhança de dois triângulos é 1, esses triângulos são
congruentes

12. EXERCÍCIOS:EXERCÍCIOS:
1. Um edifício projeta uma sombra de 10 metros, e um poste de 12
metros projeta uma sombra de 4 metros. Qual a altura do edifício,
sabendo que ele e o poste são perpendiculares.
4
10
12
=
x
4x = 120
X = 30

13. Se uma reta paralela a um dos lados de um triângulo intercepta os outros dois
lados em pontos distintos, então o triângulo que ele determina é semelhante ao
primeiro.

14. EXERCÍCIOS:EXERCÍCIOS:
2. Na figura, temos DE // BC.
a) Qual o valor de x?
b) Qual o valor de y?
c) Qual o perímetro do ∆ ABC?
d) Qual o perímetro do ∆ ADE?

15. CASO PARTICULAR DECASO PARTICULAR DE
SEMELHANÇASEMELHANÇAPara saber se dois triângulos são semelhantes não é necessário
examinar todos os lados e todos os ângulos.
Se dois triângulos possuem dois ângulos correspondentes congruentes, então
eles são semelhantes.
Dois triângulos congruentes → Triângulos semelhantes → Lados proporcionais