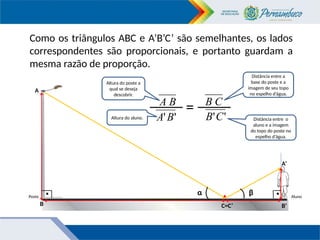
O documento aborda conceitos de semelhança de figuras planas e ângulos, explicando a definição de ângulo, medições, e as condições para que figuras sejam consideradas semelhantes, como ângulos congruentes e lados proporcionais. Também discute a proporção e a regra de três simples, além de introduzir reflexões em óptica geométrica. Por fim, são apresentados exemplos práticos de aplicação de proporções e medições em contextos da vida real.

1. MATEMÁTICA
Semelhança de figuras planas

2. GRANDEZA ÂNGULO
“Chama-se ângulo a região do plano limitada por dois
segmentos de reta que contém o mesmo ponto de origem.
Esses segmentos recebem o nome de lados do ângulo e o
ponto de origem recebe o nome de vértice do ângulo.”1
A
B
C
Ângulo formado
pelas semirretas
AB e BC

3. RETAS PARALELAS
“Duas restas distintas no plano são paralelas quando não têm
nenhum ponto em comum.
r
s
Indica-se assim: r//s
Um caso particular ocorre quando o ângulo entre duas retas é
de 90° graus ângulo. Estas são então chamadas
retas perpendiculares.”2
Indica-se assim: r s
RETAS PERPENDICULARES
r
s

4. INSTRUMENTOS DE MEDIDA
“Os instrumentos de medições sempre foram e vão ser uma
necessidade da humanidade. Medidas Exatas ou aproximadas
podem resultar em resultados adequados para as diversas
atividades. Esse tópico é tão importante que seu estudo é
objeto de um ramo da ciência conhecido como Metrologia,
que estuda o melhor método de obter a medição precisa de
diferentes grandezas, e estabelece as unidades de medição
dessas grandezas aceitas universalmente”.3

5. “Dependendo do tamanho do objeto a ser medido, são
necessários instrumentos e ou métodos diferentes para se
obter as medições. As réguas, fitas métricas, são
instrumentos adequados para medir a largura e o
comprimento, ou seja, distâncias lineares.
As figuras abaixo são instrumentos de medição de
distâncias lineares, mas existem outros aplicados para as
diversas finalidades e tipos de medições.”4
Régua5
Fita métrica6

6. “Em qualquer par de figuras semelhantes com tamanhos diferentes,
elas constitui uma cópia da outra com escala diferente.”8
A fig.2 é
semelhante a fig.1, neste caso ela é uma ampliação da fig.1,
obedecendo a uma razão de semelhança (escala).
Observe as figuras abaixo:
Fig.1 Fig.2
SEMELHANÇA DE FIGURAS PLANAS
Figuras semelhantes - ampliação 7

7. PARA QUE AS FIGURAS PLANAS SEJAM SEMELHANTES, ELAS DEVEM POSSUIR:
• Os ângulos correspondentes congruentes;
• Os lados correspondentes iguais ou proporcionais;
Vejam as figuras abaixo:
2cm
4cm
1cm
2cm
Nesse caso os ângulos correspondentes são congruentes e os
lados da figura menor é metade de seus correspondentes na
figura maior.
A semelhança indica-se assim:
A
D
B
D’
C
B’
A’
C’
D'
C'
B'
A'
ABCD
'
'
'
'
D'
D
C'
C
B'
B
A'
A
^
^
^
^
^
^
^
^


















d
d
c
c
b
b
a
a
~

8. SEMELHANÇA DE TRIÂNGULOS
“Dados dois triângulos não é necessário conferir se todos os lados
correspondentes dos mesmos são iguais ou proporcionais e ainda
se todos os ângulos correspondentes são congruentes para saber
se eles são ou não semelhantes, basta que ambos apresentem
algumas das condições necessárias, que serão mostradas a seguir:
Caso AA (Ângulo, Ângulo)
Se dois ângulos de um triângulo são congruentes a dois ângulos
de outro, os dois triângulos são semelhantes”.9
C'
B'
A'
~
ABC
'
'
C
C
B
B
^
^
^
^









A
B C C’
A’
B’

9. Caso LLL (Lado, Lado, Lado)
“Se todos os lados de um triângulo forem iguais ou
proporcionais aos lados de outro, os dois triângulos são
semelhantes”.10
C'
B'
A'
~
ABC
'
'
'







c
c
b
b
a
a
c
b’
c’
a a’
b

10. Caso LAL (Lado, Ângulo, Lado)
“Se dois triângulos possuírem um ângulo congruente formado
entre dois lados de medidas iguais ou proporcionais, os dois
triângulos são semelhantes.”11
C'
B'
A'
~
ABC
'
'
B'
B
^
^









c
c
a
a
c
c'
b
a
a'
b'
B’
B
A
C
C’
A’

11. PROPORÇÃO
“À igualdade entre duas razões equivalentes damos o nome
de proporção. Quando escrevemos estamos escrevendo
uma proporção que lê-se: 2 está para 5 assim como 4 está para
10.
10
4
5
2

O primeiro e o último termos são chamados de extremos da
proporção (2 e 10 são os extremos).
O segundo e o terceiro termos são chamados de meios da
proporção (5 e 4 são os meios).”

12. PROPRIEDADES DAS PROPORÇÕES
“1. Numa proporção o produto dos meios é igual ao produto
dos extremos:
5
x
4
10
x
2
10
4
5
2



2. Uma proporção não se altera ao alternarmos os seus
meios, ou os seus extremos:
4
10
2
5
2
4
5
10
10
5
4
2
10
4
5
2







Nesse caso, toda vez que trocarmos os termos teremos uma
nova proporção.”13

13. “3. Numa proporção, a soma (ou diferença) dos antecedentes
está para a soma (ou diferença) dos consequentes assim como
cada antecedente está para seu respectivo consequente:
5
2
5
10
2
4
10
4
5
2
e
15
6
10
5
4
2
10
4
5
2










Nesse caso o resultado da soma ou da diferença é um
número proporcional às razões dadas.”14

14. REGRA DE TRÊS SIMPLES
“Regra de três simples é um processo prático para resolver
problemas que envolvam quatro valores dos quais
conhecemos três deles. Devemos, portanto, determinar um
valor a partir dos três já conhecidos.”15
Observe:
10
4
5
x

Aplicando a primeira propriedade das proporções tem-se:
2
10
20
x
20
x
.
10
4
.
5
x
.
10
10
4
5
x









15. UM POUCO DE ÓPTICA GEOMÉTRICA
“Reflexão Regular: nesse tipo de reflexão, os raios (segmentos de
retas) refletidos, ficam paralelos uns aos outros e formam o mesmo
ângulo que os raios incidentes formam com o plano horizontal. É
esse tipo de reflexão que forma a imagem em superfícies altamente
polidas, como os espelhos, metais e em superfície d’água. A imagem
que se forma nesses meios é altamente nítida, porém, ela não pode
ser observada de diferentes posições.”16
Diagrama mostrando como ocorre a reflexão regular 17

16. Como os triângulos ABC e A’B’C’ são semelhantes, os lados
correspondentes são proporcionais, e portanto guardam a
mesma razão de proporção.
α β
A’
B’
C=C’
B
A
B
A
'
'B
A
= '
'C
B
C
B
Distância entre a
base do poste e a
imagem de seu topo
no espelho d’água.
Distância entre o
aluno e a imagem
do topo do poste no
espelho d’água.
Altura do poste a
qual se deseja
descobrir.
Altura do aluno.
Poste Aluno

17. Altura dos olhos do
aluno 1,75 metros.
Distância do aluno
até a imagem do topo
do poste no espelho
d’água 1,11 metros.
Distância entre a
base do poste e a
imagem de seu topo
no espelho d’água
5,10 metros.
Altura inacessível do
poste, a qual deseja-se
conhecer.
POSTE
DO
ALT.
75
,
1 =
10
,
5
11
,
1
SIMULAÇÃO DA SITUAÇÃO REAL

18. Utilizando a propriedade 1 da proporção e a regra de três
simples, e fazendo o produto dos meios igual ao produto dos
extremos, calcula-se assim a altura aproximada do poste.
1,75
POSTE
DO
ALT.
= 11
,
1
10
,
5
POSTE
DO
ALT.
x
1,11
=
75
,
1
x
10
,
5
POSTE
DO
ALT.
=
11
,
1
75
,
1
x
10
,
5
POSTE
DO
ALT. = metros
04
,
8

19. EXTRAS
1) Determinar a altura de uma torre de telecomunicação,
cujo topo pode ser visto por um homem, através de um
espelho d’água num ponto a 5 metros dele e a 25 metros
da base da torre. Considere que a distância dos olhos do
homes até o piso é de 1,80 metros.
2) Determinar a distância que uma pessoa, cuja altura de
seus olhos em relação ao chão é de 1,7 metros deve ficar
para que possa enxergar através de um espelho d´água o
topo de um prédio, cuja altura é de 60 metros e está a
20 metros do ponto onde esta pessoa deve ver o topo
deste prédio.