Este documento discute conceitos básicos de variáveis aleatórias reais e suas distribuições de probabilidade. Primeiro, define-se variável aleatória real e apresenta-se sua função distribuição de probabilidade cumulativa. Em seguida, discutem-se propriedades das variáveis aleatórias discretas, contínuas e mistas, e introduz-se a função densidade de probabilidade. Por fim, exemplificam-se distribuições como uniforme, normal e exponencial.

1. Departamento DDDDDDDeeeeeeepppppppaaaaaaarrrrrrrtttttttaaaaaaammmmmmmeeeeeeennnnnnntttttttooooooo ddddddddeeeeeeee IIIIIIIInnnnnnnnffffffffoooooooorrrrrrrrmmmmmmmmááááááááttttttttiiiiiiiiccccccccaaaaaaaa
DDDDDDDDiiiiiiiisssssssscccccccciiiiiiiipppppppplllllllliiiiiiiinnnnnnnnaaaaaaaa::::::::
MMMMooooddddeeeellllaaaaggggeeeemmmm AAAAnnnnaaaallllííííttttiiiiccccaaaa ddddoooo
DDDDeeeesssseeeemmmmppppeeeennnnhhhhoooo ddddeeee SSSSiiiisssstttteeeemmmmaaaassss
ddddeeee CCCCoooommmmppppuuuuttttaaaaççççããããoooo
Variável Aleatória
Prof. Sérgio Colcher
colcher@inf.puc-rio.br
1
CCCCooooppppyyyyrrrriiiigggghhhhtttt 1111999999999999-2222000000007777 bbbbyyyy TTTTeeeelllleeeeMMMMííííddddiiiiaaaa LLLLaaaabbbb....
Variável Aleatória Real
Modelagem Analítica
O espaço de amostras W foi definido como o
conjunto de todos os possíveis resultados de uma
experiência
• Os elementos de W não são necessariamente
numéricos
–Mas é quase sempre interessante que W tenha uma
respresentação numérica
– Pode-se associar a cada ponto w Î W um número real
x(w)
– Uma função x que mapeia os pontos de W em R é
denominada uma variável aleatória (v.a) real.
2
Variável Aleatória Real
Modelagem Analítica
Medida de Probabilidade
3
Fenômeno
Experiência
w
W
A
B
A
A B
R
0 1
R
Variável Aleatória
Variável Aleatória Real
Modelagem Analítica
w w
= ÎW £ Î Î
i) os conjuntos { : ( ) }
isto é, são eventos válidos para qualquer número real
A X
w w
ÎW = ¥ =
ii) P ({ : x
( ) }) 0
w w
ÎW = −¥ =
4
Definição
• Uma v.a. real x é uma função
tal que
:
R
R
W ®
w
®
x
({ : ( ) }) 0
P x
A x X ; X
x
x A R

2. Variável Aleatória Real
Modelagem Analítica
Medida de Probabilidade
5
Fenômeno
Experiência
w
W
A
B
A
A B
R
0 1
R
Variável Aleatória
?
Variável Aleatória Real
Modelagem Analítica
Como é um evento, é possível atribuir
uma probabilidade ao subconjunto : dos
Reais da seguinte maneira
• Isto garante que qualquer intervalo I de R está
também associado a uma probabilidade
6
{ }
{ }
P {x x X} P({:x() X})
x x X
:x() X
£ = £
£
£
( : )
Variável Aleatória Real
Modelagem Analítica
Medida de Probabilidade
7
Fenômeno
Experiência
w
W
A
B
A
A B
R
0 1
R
I
Modelagem Analítica
Tipos de V.A.s
8
V.A. Discreta
V.A. Contínua
V.A. Mista

3. Modelagem Analítica
V.A. Discreta
Diz-se que uma v.a. é discreta quando o seu contradomínio Wx
é um conjunto de pontos isolados (finito ou infinito, porém
numerável). Isto significa que
{ , ,…} 1 2 X X x W =
• A partir dessa definição é possível verificar a existência de eventos cujo
conjunto contém apenas um elemento: Xi
• Como a cada valor da v.a. associa-se uma medida de probabilidade, pode-se
({ })
w ÎW : (w) = = ; =
1,2,…
P x X p i
com a condição
9
escrever que
=
i
i
i i
p
1
• O conjunto {p1, p2, ...} é a distribuição de probabilidade da v.a discreta.
– Não confundir com a ““Função Distribuição de Probabilidade (FDP)””
que será apresentada mais adiante.
Modelagem Analítica
V.A. Contínua
Uma v.a. x cujo contradomínio Wx é contínuo, é uma
v.a. contínua.
• Wx é agora um conjunto não numerável e se a
probabilidade associada a cada X Î Wx for maior que
zero, será violada a condição axiomática de que P(W)=1
– Neste caso, é mais apropriado definir uma medida de
probabilidade associada a intervalos, de tal forma que a
função px, definida em Wx, é tal que, para qualquer intervalo
I Ì R
Î =
x P(x I ) p (X )dX
10
I
Modelagem Analítica
V.A. Contínua
Uma v.a. contínua satisfaz a condição
P(x = X ) = 0
• É importante ressaltar a diferença entre evento vazio e
evento com probabilidade zero
– Por exemplo, para uma v.a. contínua, o evento {x = X} tem
probabilidade zero mas não é vazio pois contém o ponto X.
11
Modelagem Analítica
V.A. Mista
Uma v.a. x, cujo contradomínio Wx é não
numerável, mas que contém um subconjunto (finito
ou infinito numerável) no qual cada um de seus
pontos tem probabilidade maior que zero é
denominado de v.a. mista.
12

4. Função Distribuição de Probabilidade (FDP)
Modelagem Analítica
A Função Distribuição de Probabilidade (FDP)
também conhecida como Função de Distribuição
Cumulativa (FDC) associada a uma v.a. real x é a
função definida por
( ) ( )
R ® R
• Lembre que na definição de v.a. foi exigido que os
subconjuntos {x £ X} fossem eventos
13
:
x F X P x X
F
x
x
® = £
Modelagem Analítica
Exemplo
Considere o experimento de lançar um dado com seis
faces fi, i = 1, ……, 6, onde os resultados de todas as faces
são equiprováveis
Seja x, uma variável aleatória real, com o seguinte
W®
R
® =
( ) i i f x f i
14
mapeamento:
Esboçar a FDP de x: Fx(X)
Modelagem Analítica
Exemplo
Considere o experimento de lançar um dado com seis
faces fi, i = 1, ……, 6, onde os resultados de todas as faces
são equiprováveis
Seja x, uma variável aleatória real, com o seguinte
W®
R
2 f i ® x ( f i ) = ( i
−
3) 15
mapeamento:
Esboçar a FDP de x: Fx(X)
Modelagem Analítica
Propriedades das FDPs
16

5. Modelagem Analítica
Exemplo
Uma v.a. tem FDC dada por
17
Desejamos obter
i. Fy(0)
ii. P(0y)
iii. P(5y10)
iv. P(y=0)
Fy(Y)
1
- 5 5 10 15 20
Y
Modelagem Analítica
Forma Geral da FDP
Toda Função Distribuição de Probabilidade Fx(X) pode
( ) ( ) ( ) x x x F X = C X + D X
D X =P x = X u X − X
19
ser escrita como
onde Cx é uma função contínua e Dx é um somatório de
funções degrau
( ) ( ) ( ) x i i
i
Função Densidade de Probabilidade (f.d.p.)
Modelagem Analítica
Para uma v.a. x com F.D.P Fx, define-se como
f.d.p. a função fx dada por
( )
dF X
( ) x
x
• Quando a v.a. é discreta, tem-se
= −
A função que descreve P(x = Xi)
20
f X
dX
=
( )
( )
dF X
P( ) ( )
x
=
=
= = −
( ) P( ) ( )
x
i i
i
x i i
i
f X
dX
d x X u X X
dX
f X x X d X X
é denominada de função de massa
de probabilidade (f.m.p.).
Modelagem Analítica
Propriedades da f.d.p.
( ) ( )
f Y dY F X
( ) ( )
−¥
F Y F X
21
X
x x
X
x x
−¥
=
=
i)

6. Modelagem Analítica
Propriedades da f.d.p.
( ) 1
( ) 1 0 1
22
x
−¥
x
f Y dY
¥
F Y
¥
−¥
=
= − =
ii)
Modelagem Analítica
Propriedades da f.d.p.
23
iii) ³
( ) 0
f X
( ) é não decrescente
x
F X
x
Modelagem Analítica
Propriedades da f.d.p.
iv) f X dX = P xÎI
( ) ( ) x
Por exemplo, para I = (a,b]
Î = −
P x a b F b F a
−¥ −¥
−¥
24
I
( ( , ]) ( ) ( )
( ) ( )
( ) ( )
( )
x x
b a
b
a
b
a
f X dX f X dX
f X dX f X dX
f X dX
−¥
= −
= +
=
Modelagem Analítica
Exemplo
Uma v.a. tem FDC dada por
Fy(Y)
1
i. Esboçar a fdp fy(Y)
ii. A partir do gráfico de (i), calcular
25
a. Fy(0)
b. P(y0)
c. P(5y10)
- 5 5 10 15 20
Y

7. Modelagem Analítica
Exemplo de Distribuições
26
Contínuas
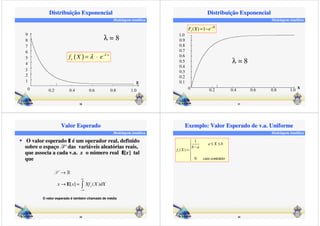
• Uniforme
• Exponencial
• Gaussiana (ou Normal)
Discretas
• Bernoulli
• Binomial
• Geométrica
• Poisson
Exemplo: Distribuição Uniforme
Modelagem Analítica
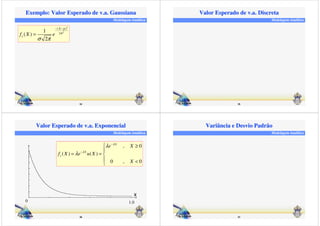
Uma v.a. x é dita uniformemente distribuída no
intervalo [a,b] quando sua f.d.p é dada por
27
1
( )
0 caso contrário
x
a X b
b a
f X
£ £
−
=

8. fx(X)
X
a b
1
b − a
Fx(X)
X
a b
1
Distribuição Normal (Gaussiana)
Modelagem Analítica
28
0
0 , 5
0
1
μ
s
=
=
μ
s
=
=
3
2
μ
s
=
=
( ) x f X
2
( )
1
2
2 ( )
2
X
x f X e
μ
s
s p
− −
=
Modelagem Analítica
Distribuição Exponencial
X
, 0
X
X
( ) ( )
F X f Y dY
x y
X
e dY l l
( ) ( ) 1 , 0
29
1 ( )
0 , 0
X
x
e X
F X e u x
X
l
l
−
−
− ³
= − =

9. ( ) ( )
0 , 0
X
x
e X
f X e u X
X
l
l
l
l
−
−
³
= =