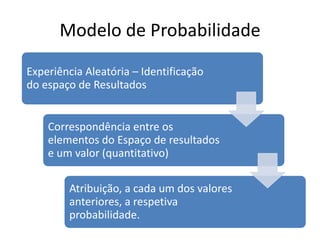
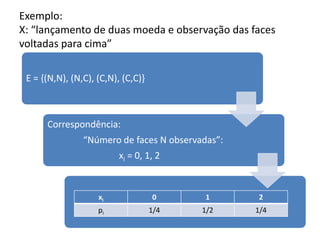
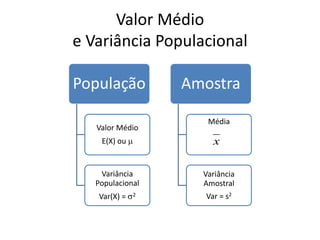
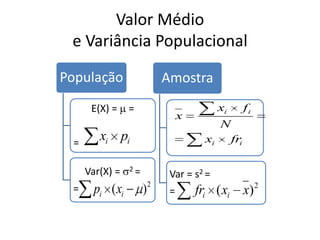
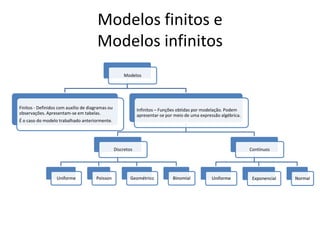
O documento descreve os principais modelos de probabilidade. Apresenta os conceitos de modelo discreto, contínuo, finito e infinito. Explica como calcular a média e variância populacional para modelos de probabilidade e fornece exemplos de modelos discretos como o uniforme, de Poisson, geométrico e binomial. Também explica modelos contínuos como o uniforme, exponencial e normal.

1. Modelo de Probabilidade
Definição de Modelo de Probabilidade
Valor médio e
Variância Populacional

2. Modelo de Probabilidade
• É um modelo que descreve matematicamente
um fenómeno aleatório em duas partes:
primeiro, identifica os valores da variável
aleatória e, em seguida, associa a cada um
deles o valor da respetiva probabilidade. Cada
uma destas probabilidades tem que estar
entre 0 e 1 (ou 0% e 100%) e a soma de todas
as probabilidades é 1 (ou 100%).

3. Modelo de Probabilidade
Experiência Aleatória – Identificação
do espaço de Resultados
Correspondência entre os
elementos do Espaço de resultados
e um valor (quantitativo)
Atribuição, a cada um dos valores
anteriores, a respetiva
probabilidade.

4. Exemplo:
X: “lançamento de duas moeda e observação das faces
voltadas para cima”
E = {(N,N), (N,C), (C,N), (C,C)}
Correspondência:
“Número de faces N observadas”:
xi = 0, 1, 2
xi 0 1 2
pi 1/4 1/2 1/4

5. Valor Médio
e Variância Populacional
População Amostra
Média
Valor Médio
E(X) ou x
Variância Variância
Populacional Amostral
Var(X) = 2 Var = s2

6. Valor Médio
e Variância Populacional
População Amostra
E(X) = = xi fi
x
N
=
xi pi xi fri
Var(X) = 2=
Var = s2 =
= pi ( xi )2 = fri ( xi x) 2

7. Exemplo:
X: “lançamento de duas moeda e observação das faces
voltadas para cima”
xi 0 1 2
pi 1/4 1/2 1/4
1 1 1
E(X) = = xi pi 0 1 2 1
4 2 4
Var(X) = 2=
2 1 2 1 2 1 2
pi ( xi ) 0 1 1 1 2 1 0,5
4 2 4
0,5 0,707

8. Modelo de Probabilidade
Modelos discretos/Modelos contínuos
Modelos finitos/Modelos infinitos

9. Modelo Discreto
• Associado a uma variável aleatória discreta.
– Exemplos:
• N.º de faces Nacionais observadas no lançamento de
duas moedas (modelo finito);
• N.º de telefonemas atendidos por hora na central
telefónica da EBSO (modelo infinito – modelo de
Poisson).

10. Modelo Contínuo
• Associado a uma variável aleatória contínua.
– Exemplos:
• Tempo até ser atendido na fila supermercado (modelo
infinito – modelo Exponencial);
• Duração de um anuncio publicitário (modelo infinito –
modelo Uniforme);
• Altura dos rapazes aos 18 anos (modelo infinito –
modelo normal).

11. Modelos finitos e
Modelos infinitos
Modelos
Finitos - Definidos com auxílio de diagramas ou Infinitos – Funções obtidas por modelação. Podem
observações. Apresentam-se em tabelas. apresentar-se por meio de uma expressão algébrica.
É o caso do modelo trabalhado anteriormente.
Discretos Contínuos
Uniforme Poisson Geométrico Binomial Uniforme Exponencial Normal

12. Modelos teóricos (infinitos)
• Modelos discretos:
– Modelo uniforme – todos os acontecimentos do espaço
têm a mesma probabilidade.
– Modelo de Poisson – determina a probabilidade se
observarem um determinado número de vezes um dado
acontecimento de uma experiência num determinado
período de tempo.
– Modelo Geométrico – determina a probabilidade de o
número de realizações de dada experiência até se obter
um valor dado ser igual a k.
– Modelo Binomial – Determina a probabilidade de, em n
repetições de uma certa experiência em iguais
condições, se observar exactamente k vezes o
acontecimento xi.

13. Modelos teóricos (infinitos)
• Modelos contínuos:
– Modelo Uniforme – a probabilidade distribui-se de
igual forma num dado intervalo de tempo.
– Modelo Exponencial – determina a probabilidade de o
tempo de espera para a realização de dado
acontecimento se situar num determinado intervalo.
– Modelo Normal – Modela a maioria das distribuições
contínuas e aproxima de forma adequada as
distribuições discretas quando o número de
realizações da experiência que lhes está associada é
grande (>20).

14. Modelos teóricos (infinitos)
• Para cada uma das variáveis aleatórias
caracterizadas pelos modelos referidos vamos
estudar:
– A Expressão do modelo (se X …, então,
P(X=k)=…)
– O valor médio (E(X)= =…)
– A variância e o desvio padrão populacional
(Var(X)=… e =…)
– Como usar a calculadora para calcular
probabilidades com base em cada um dos
modelos.

15. Modelos infinitos discretos:
Modelo Uniforme
• Seja X uma variável aleatória cujo o espaço de
resultados é composto por n acontecimentos
elementares equiprováveis. Então:
– X U (n) e P(X=k) = 1/n
– O valor médio (E(X)= = média entre o maior e o
menor valor da v.a.)
– A variância e o desvio padrão populacional
calculam-se usando as listas e o “varstat” do menu
STAT da calculadora.

16. Modelos infinitos discretos:
Modelo de Poisson
• Seja X uma variável aleatória que descreve o número
de realizações de um dado acontecimento num
determinado período de tempo, sobre a qual se sabe
que a média de realizações é . Então, X é modelada
por uma distribuição de Poisson:
k
–X P( ) e P(X=k) = e , k 0, 1, 2, 3,...
k!
– O valor médio é E(X)= =
– A variância é Var(X)=
– Calculadora: Seja X P(5); então, P(X=6) = 0,146
(2nd/distr/poissonpdf(5,6)/enter); P(2≤X≤6) = P(X ≤ 6)-P(X
≤1) = 0.7621-0.0404 =0.7217 (poissoncdf(5,6)-
poissoncdf(5,1)/enter)

17. Modelos infinitos discretos:
Modelo Geométrico
• Seja X uma variável aleatória que modela o número de
repetições de uma determinada experiência necessárias
até que se obtenha o resultado xi, em que a probabilidade
de ocorrer xi é p (entre 0 e 1) e de não ocorrer é 1-p.
Então, X é modelada por uma distribuição Geométrica de
parâmetro p:
–X Geom(p) e P(X=k)(1 p)k
= 1
p
– O valor médio é E(X)= = 1/p
– A variância é Var(X)= (1-p)/p2
– Calculadora: Seja X Geom(0.3); então, P(X=6) = 0.75x0.3 =
0.05 (ou 2nd/distr/Geometpdf(0.3,6)/enter); P(2≤X≤6) = P(X ≤
6)-P(X ≤1) = Geometcdf(0.3,6)-Geometcdf(0.3,1)/enter=0.5824

18. Modelos infinitos discretos:
Modelo Binomial
• Seja X uma variável aleatória que modela a
probabilidade de um acontecimento xi se realizar k
vezes em n realizações de uma dada experiência. A
probabilidade de xi é p (entre 0 e 1) e de não acontecer
xi é q = 1-p. Então, X é modelada por uma distribuição
Binomial de parâmetros n e p:
Bi(n,p) e P(X=k) = Ckn p k (1 p)n k
–X
– O valor médio é E(X)= = n x p
– A variância é Var(X)= n x p x (1- p) = n x p x q
– Calculadora: Seja X Bi(5, 0.3); então, P(X=3) = 0.1323
(2nd/distr/Binompdf(5,0.3,3)/enter); P(2≤X≤4) = P(X ≤ 4)-P(X
≤1) = Binomcdf(5,0.3,4)-Binomcdf(5,0.3,1)/enter=0.4694

19. Modelos infinitos contínuos
• Um modelo de probabilidades diz-se contínuo se
lhe está associada uma v. a. Contínua. Neste caso, o
domínio do modelo será o intervalo ou intervalos
onde está definida a variável. À função modelo
chamamos função densidade e o seu gráfico situa-
se completamente acima do eixo dos xx.

20. Modelos discretos vs Modelos contínuos
Discretos Contínuos
Área total
Soma das
compreendida entre o
probabilidades
gráfico da função
associadas a cada valor
densidade e o eixo dos
da v.a. é 1
xx é 1
P(a≤X≤b) = área
compreendida entre o
P(a≤X≤b) = P(X=a) +
gráfico e o eixo dos xx
P(X=a+1) + (…) +
na barra
P(X=b)
correspondente ao
intervalo [a , b].

21. Modelos infinitos contínuos:
Modelo Uniforme
• Associado a v.a. contínuas que se encontram
uniformemente distribuídas num intervalo [a,b], isto
é, uma v.a. em que, dados quaisquer dois valores do
intervalo, a probabilidade que lhes está associada é
exatamente a mesma. Seja X uma v.a. Uniforme em
[a,b]. Então:
d c
–X U[a,b] e P(c ≤ X ≤ d) = , a c d b
b a
(área do retângulo de lados d-c e b-a)
– O valor médio é E(X)= = (a+b)/2
– Obs.: P(a ≤ X ≤ b) = 1.

22. Modelos infinitos contínuos:
Modelo Exponencial
• Seja X uma variável aleatória que modela a probabilidade de
o tempo de espera (entre chegadas numa fila de
espera, entre falhas num dispositivo eletrónico, entre
chegadas de um pedido a um servidor de Internet, etc.) se
situar num dado intervalo, então X é modelada por uma
distribuição Exponencial de parâmetro :
–X Exp( ) e P(a ≤ X ≤ b) =e a
e b
– O valor médio é E(X)= =1/
– Não existe esta distribuição na calculadora. Assim, seja
X Exp(0.2) (significa que, por exemplo, o tempo médio de
espera é 1/0.2 = 5); e 0.2 2 P(2 0.2X6≤ 6) .369
então, e ≤ 0=

23. Modelos infinitos contínuos:
Modelo Normal
• Baseia-se na distribuição Normal, que é a mais
importante distribuição contínua, já estudada no
10.º ano (características no manual).
• Se X N( , ), então:
– O valor médio é E(X)=
– A variância é Var(X)= 2;
– é o desvio-padrão populacional
– Calculadora: P(a≤X≤b) = normalcdf(a,b, , ).
Exemplo:
Seja X N(5, 0.7); então, P(4≤X≤6) = normalcdf(4,6,5,0.7)=0.8469