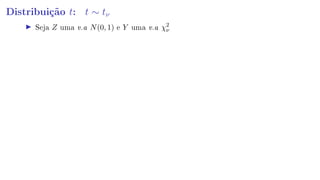Este documento apresenta uma agenda para discutir vários tópicos relacionados a variáveis aleatórias, incluindo: (1) distribuição uniforme, (2) média e variância da distribuição uniforme, (3) distribuição normal, (4) distribuição F, e (5) distribuição t de Student. O documento também fornece uma introdução sobre variáveis aleatórias e suas funções de distribuição e densidade. Por fim, discute a distribuição uniforme em mais detalhes, definindo sua função de densidade, esperança matemática e







![Agenda
Variável Aleatória: função de distribuição e de densidade;
0 Distribuição Uniforme X ∼ U[a, b];](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-8-320.jpg)
![Agenda
Variável Aleatória: função de distribuição e de densidade;
0 Distribuição Uniforme X ∼ U[a, b];
1 Média e Variância: X ∼ U[a, b];](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-9-320.jpg)
![Agenda
Variável Aleatória: função de distribuição e de densidade;
0 Distribuição Uniforme X ∼ U[a, b];
1 Média e Variância: X ∼ U[a, b];
2 Distribuição Normal](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-10-320.jpg)
![Agenda
Variável Aleatória: função de distribuição e de densidade;
0 Distribuição Uniforme X ∼ U[a, b];
1 Média e Variância: X ∼ U[a, b];
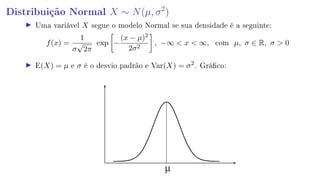
2 Distribuição Normal X ∼ N(µ, σ2
);](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-11-320.jpg)
![Agenda
Variável Aleatória: função de distribuição e de densidade;
0 Distribuição Uniforme X ∼ U[a, b];
1 Média e Variância: X ∼ U[a, b];
2 Distribuição Normal X ∼ N(µ, σ2
);
3 Distribução F de probabilidade;](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-12-320.jpg)
![Agenda
Variável Aleatória: função de distribuição e de densidade;
0 Distribuição Uniforme X ∼ U[a, b];
1 Média e Variância: X ∼ U[a, b];
2 Distribuição Normal X ∼ N(µ, σ2
);
3 Distribução F de probabilidade;
4 Distribuição t de Student.](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-13-320.jpg)
![Agenda
Variável Aleatória: função de distribuição e de densidade;
0 Distribuição Uniforme X ∼ U[a, b];
1 Média e Variância: X ∼ U[a, b];
2 Distribuição Normal X ∼ N(µ, σ2
);
3 Distribução F de probabilidade;
4 Distribuição t de Student.](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-14-320.jpg)










![Introdução
i. Variável Aleatória: Seja (Ω, F, P) um espaço de probabilidade.
Denominamos variável aleatória, qualquer função: X : Ω → R tal que
X−1
(I) = {ω ∈ Ω : X(ω) ∈ I} ∈ F
uma variável aleatória (v.a) é um característico numérico do resultado de
um experimento aleatório.
Uma variável aleatória X em um espaço de probabilidade (Ω, F, P) é
uma função real denida no espaço Ω tal que [X ≤ x]](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-25-320.jpg)
![Introdução
i. Variável Aleatória: Seja (Ω, F, P) um espaço de probabilidade.
Denominamos variável aleatória, qualquer função: X : Ω → R tal que
X−1
(I) = {ω ∈ Ω : X(ω) ∈ I} ∈ F
uma variável aleatória (v.a) é um característico numérico do resultado de
um experimento aleatório.
Uma variável aleatória X em um espaço de probabilidade (Ω, F, P) é
uma função real denida no espaço Ω tal que [X ≤ x] é evento aleatório
∀x ∈ R; i.e,](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-26-320.jpg)
![Introdução
i. Variável Aleatória: Seja (Ω, F, P) um espaço de probabilidade.
Denominamos variável aleatória, qualquer função: X : Ω → R tal que
X−1
(I) = {ω ∈ Ω : X(ω) ∈ I} ∈ F
uma variável aleatória (v.a) é um característico numérico do resultado de
um experimento aleatório.
Uma variável aleatória X em um espaço de probabilidade (Ω, F, P) é
uma função real denida no espaço Ω tal que [X ≤ x] é evento aleatório
∀x ∈ R; i.e,
X : Ω → R é variável aleatória se [X ≤ x] ∈ F, ∀x ∈ R](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-27-320.jpg)


![Introdução
Sendo X uma va em (Ω, F, P) sua função de distribuição é denida por:
FX(x) = P(X ∈ (−∞, x])) = P(X ≤ x)](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-30-320.jpg)
![Introdução
Sendo X uma va em (Ω, F, P) sua função de distribuição é denida por:
FX(x) = P(X ∈ (−∞, x])) = P(X ≤ x)
A partir da f.d obtemos quaisquer informações acerca da v.a.](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-31-320.jpg)
![Introdução
Sendo X uma va em (Ω, F, P) sua função de distribuição é denida por:
FX(x) = P(X ∈ (−∞, x])) = P(X ≤ x)
A partir da f.d obtemos quaisquer informações acerca da v.a.
Obtemos também a função de densidade de probabilidade](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-32-320.jpg)
![Introdução
Sendo X uma va em (Ω, F, P) sua função de distribuição é denida por:
FX(x) = P(X ∈ (−∞, x])) = P(X ≤ x)
A partir da f.d obtemos quaisquer informações acerca da v.a.
Obtemos também a função de densidade de probabilidade ou a função de
probabilidade](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-33-320.jpg)
![Introdução
Sendo X uma va em (Ω, F, P) sua função de distribuição é denida por:
FX(x) = P(X ∈ (−∞, x])) = P(X ≤ x)
A partir da f.d obtemos quaisquer informações acerca da v.a.
Obtemos também a função de densidade de probabilidade ou a função de
probabilidade , que está associada à uma função de distribuição;](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-34-320.jpg)
![Introdução
Sendo X uma va em (Ω, F, P) sua função de distribuição é denida por:
FX(x) = P(X ∈ (−∞, x])) = P(X ≤ x)
A partir da f.d obtemos quaisquer informações acerca da v.a.
Obtemos também a função de densidade de probabilidade ou a função de
probabilidade , que está associada à uma função de distribuição;](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-35-320.jpg)



![Exame 2019 Questão 1
Julgue como verdadeiras ou falsas as armativas que se seguem:
0. Uma dada variável aleatória com distribuição uniforme no intervalo [2, 5] tem
média igual a 3, 50.](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-39-320.jpg)
![Exame 2019 Questão 1
Julgue como verdadeiras ou falsas as armativas que se seguem:
0. Uma dada variável aleatória com distribuição uniforme no intervalo [2, 5] tem
média igual a 3, 50.
1. Uma dada variável aleatória com distribuição uniforme no intervalo [2, 5] tem
variância igual a 0, 75.](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-40-320.jpg)
![Exame 2019 Questão 1
Julgue como verdadeiras ou falsas as armativas que se seguem:
0. Uma dada variável aleatória com distribuição uniforme no intervalo [2, 5] tem
média igual a 3, 50.
1. Uma dada variável aleatória com distribuição uniforme no intervalo [2, 5] tem
variância igual a 0, 75.
2. Seja X uma variável aleatória com distribuição normal, com média 2 e
variância 5, então Z =
X − 2
5
também apresenta distribuição normal, com
média 0 e variância 1.](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-41-320.jpg)
![Exame 2019 Questão 1
Julgue como verdadeiras ou falsas as armativas que se seguem:
0. Uma dada variável aleatória com distribuição uniforme no intervalo [2, 5] tem
média igual a 3, 50.
1. Uma dada variável aleatória com distribuição uniforme no intervalo [2, 5] tem
variância igual a 0, 75.
2. Seja X uma variável aleatória com distribuição normal, com média 2 e
variância 5, então Z =
X − 2
5
também apresenta distribuição normal, com
média 0 e variância 1.
3. Sejam Z1 e Z2 duas variáveis aleatórias independentes com distribuição
quiquadrado, então W =
Z1
Z2
apresenta distribuição F.](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-42-320.jpg)
![Exame 2019 Questão 1
Julgue como verdadeiras ou falsas as armativas que se seguem:
0. Uma dada variável aleatória com distribuição uniforme no intervalo [2, 5] tem
média igual a 3, 50.
1. Uma dada variável aleatória com distribuição uniforme no intervalo [2, 5] tem
variância igual a 0, 75.
2. Seja X uma variável aleatória com distribuição normal, com média 2 e
variância 5, então Z =
X − 2
5
também apresenta distribuição normal, com
média 0 e variância 1.
3. Sejam Z1 e Z2 duas variáveis aleatórias independentes com distribuição
quiquadrado, então W =
Z1
Z2
apresenta distribuição F.
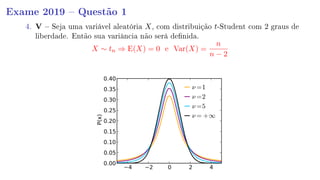
4. Seja uma variável aleatória X, com distribuição t-Student com 2 graus de
liberdade. Então sua variância não será denida.](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-43-320.jpg)
![Distribuição Uniforme[a, b]](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-44-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-45-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-46-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Valor esperado ou Esperança Matemática:](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-47-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Valor esperado ou Esperança Matemática:
E(X) =
b
a
x · f(x) dx](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-48-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Valor esperado ou Esperança Matemática:
E(X) =
b
a
x · f(x) dx
=
b
a
x
b − a
dx](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-49-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Valor esperado ou Esperança Matemática:
E(X) =
b
a
x · f(x) dx
=
b
a
x
b − a
dx =
x2
2(b − a)
b
a](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-50-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Valor esperado ou Esperança Matemática:
E(X) =
b
a
x · f(x) dx
=
b
a
x
b − a
dx =
x2
2(b − a)
b
a
=
b2
2(b − a)](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-51-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Valor esperado ou Esperança Matemática:
E(X) =
b
a
x · f(x) dx
=
b
a
x
b − a
dx =
x2
2(b − a)
b
a
=
b2
2(b − a)
−
a2
2(b − a)](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-52-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Valor esperado ou Esperança Matemática:
E(X) =
b
a
x · f(x) dx
=
b
a
x
b − a
dx =
x2
2(b − a)
b
a
=
b2
2(b − a)
−
a2
2(b − a)
=
b2 − a2
2(b − a)](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-53-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Valor esperado ou Esperança Matemática:
E(X) =
b
a
x · f(x) dx
=
b
a
x
b − a
dx =
x2
2(b − a)
b
a
=
b2
2(b − a)
−
a2
2(b − a)
=
b2 − a2
2(b − a)
=
(b − a)(b + a)](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-54-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Valor esperado ou Esperança Matemática:
E(X) =
b
a
x · f(x) dx
=
b
a
x
b − a
dx =
x2
2(b − a)
b
a
=
b2
2(b − a)
−
a2
2(b − a)
=
b2 − a2
2(b − a)
=
(b − a)(b + a)
2(b − a)](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-55-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Valor esperado ou Esperança Matemática:
E(X) =
b
a
x · f(x) dx
=
b
a
x
b − a
dx =
x2
2(b − a)
b
a
=
b2
2(b − a)
−
a2
2(b − a)
=
b2 − a2
2(b − a)
=
(b − a)(b + a)
2(b − a)
=
(b − a)(b + a)
2(b − a)](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-56-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Valor esperado ou Esperança Matemática:
E(X) =
b
a
x · f(x) dx
=
b
a
x
b − a
dx =
x2
2(b − a)
b
a
=
b2
2(b − a)
−
a2
2(b − a)
=
b2 − a2
2(b − a)
=
(b − a)(b + a)
2(b − a)
=
(b − a)(b + a)
2(b − a)
E(X) =
a + b
2](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-57-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-58-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Valor esperado de X2
:](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-59-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Valor esperado de X2
:
E(X2
)](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-60-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Valor esperado de X2
:
E(X2
) =
b
a
x2
· f(x) dx](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-61-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Valor esperado de X2
:
E(X2
) =
b
a
x2
· f(x) dx
=
b
a
x2
b − a
dx](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-62-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Valor esperado de X2
:
E(X2
) =
b
a
x2
· f(x) dx
=
b
a
x2
b − a
dx =
x3
3(b − a)
b
a](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-63-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Valor esperado de X2
:
E(X2
) =
b
a
x2
· f(x) dx
=
b
a
x2
b − a
dx =
x3
3(b − a)
b
a
=
b3
3(b − a)](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-64-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Valor esperado de X2
:
E(X2
) =
b
a
x2
· f(x) dx
=
b
a
x2
b − a
dx =
x3
3(b − a)
b
a
=
b3
3(b − a)
−
a3
3(b − a)](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-65-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Valor esperado de X2
:
E(X2
) =
b
a
x2
· f(x) dx
=
b
a
x2
b − a
dx =
x3
3(b − a)
b
a
=
b3
3(b − a)
−
a3
3(b − a)
=
b3 − a3](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-66-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Valor esperado de X2
:
E(X2
) =
b
a
x2
· f(x) dx
=
b
a
x2
b − a
dx =
x3
3(b − a)
b
a
=
b3
3(b − a)
−
a3
3(b − a)
=
b3 − a3
3(b − a)](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-67-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Valor esperado de X2
:
E(X2
) =
b
a
x2
· f(x) dx
=
b
a
x2
b − a
dx =
x3
3(b − a)
b
a
=
b3
3(b − a)
−
a3
3(b − a)
=
b3 − a3
3(b − a)
=
(b − a)(b2 + ab + a2)](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-68-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Valor esperado de X2
:
E(X2
) =
b
a
x2
· f(x) dx
=
b
a
x2
b − a
dx =
x3
3(b − a)
b
a
=
b3
3(b − a)
−
a3
3(b − a)
=
b3 − a3
3(b − a)
=
(b − a)(b2 + ab + a2)
3(b − a)](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-69-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Valor esperado de X2
:
E(X2
) =
b
a
x2
· f(x) dx
=
b
a
x2
b − a
dx =
x3
3(b − a)
b
a
=
b3
3(b − a)
−
a3
3(b − a)
=
b3 − a3
3(b − a)
=
(b − a)(b2 + ab + a2)
3(b − a)
=
(b − a)(b2 + ab + a2)
3(b − a)](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-70-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Valor esperado de X2
:
E(X2
) =
b
a
x2
· f(x) dx
=
b
a
x2
b − a
dx =
x3
3(b − a)
b
a
=
b3
3(b − a)
−
a3
3(b − a)
=
b3 − a3
3(b − a)
=
(b − a)(b2 + ab + a2)
3(b − a)
=
(b − a)(b2 + ab + a2)
3(b − a)
E(X2
) =
b2 + ab + a2
3](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-71-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-72-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Variância Var(X) = E(X2
) − E(X)2
:](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-73-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Variância Var(X) = E(X2
) − E(X)2
:
Var(X)](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-74-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Variância Var(X) = E(X2
) − E(X)2
:
Var(X) =
b2 + ab + a2
3](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-75-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Variância Var(X) = E(X2
) − E(X)2
:
Var(X) =
b2 + ab + a2
3
−
a + b
2
2](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-76-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Variância Var(X) = E(X2
) − E(X)2
:
Var(X) =
b2 + ab + a2
3
−
a + b
2
2
=
4b2 + 4ab + 4a2
12](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-77-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Variância Var(X) = E(X2
) − E(X)2
:
Var(X) =
b2 + ab + a2
3
−
a + b
2
2
=
4b2 + 4ab + 4a2
12
−
a2 + 2ab + b2
4](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-78-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Variância Var(X) = E(X2
) − E(X)2
:
Var(X) =
b2 + ab + a2
3
−
a + b
2
2
=
4b2 + 4ab + 4a2
12
−
a2 + 2ab + b2
4
=
4b2 + 4ab + 4a2
12](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-79-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Variância Var(X) = E(X2
) − E(X)2
:
Var(X) =
b2 + ab + a2
3
−
a + b
2
2
=
4b2 + 4ab + 4a2
12
−
a2 + 2ab + b2
4
=
4b2 + 4ab + 4a2
12
−
3a2 + 6ab + 3b2
12](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-80-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Variância Var(X) = E(X2
) − E(X)2
:
Var(X) =
b2 + ab + a2
3
−
a + b
2
2
=
4b2 + 4ab + 4a2
12
−
a2 + 2ab + b2
4
=
4b2 + 4ab + 4a2
12
−
3a2 + 6ab + 3b2
12
=
b2 − 2ab + a2
12](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-81-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Variância Var(X) = E(X2
) − E(X)2
:
Var(X) =
b2 + ab + a2
3
−
a + b
2
2
=
4b2 + 4ab + 4a2
12
−
a2 + 2ab + b2
4
=
4b2 + 4ab + 4a2
12
−
3a2 + 6ab + 3b2
12
=
b2 − 2ab + a2
12
=
(b − a)2
12](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-82-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-83-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Média e Variância:](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-84-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Média e Variância:
E(X) =
a + b
2](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-85-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Média e Variância:
E(X) =
a + b
2
e Var(X) =
(b − a)2
12](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-86-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Média e Variância:
E(X) =
a + b
2
e Var(X) =
(b − a)2
12
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
0. Uma dada variável aleatória com distribuição uniforme no intervalo [2, 5] tem
média igual a 3, 50.](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-87-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Média e Variância:
E(X) =
a + b
2
e Var(X) =
(b − a)2
12
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
0. Uma dada variável aleatória com distribuição uniforme no intervalo [2, 5] tem
média igual a 3, 50.
1. Uma dada variável aleatória com distribuição uniforme no intervalo [2, 5] tem
variância igual a 0, 75.](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-88-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Média e Variância:
E(X) =
a + b
2
e Var(X) =
(b − a)2
12
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
0. Uma dada variável aleatória com distribuição uniforme no intervalo [2, 5] tem
média igual a 3, 50.
1. Uma dada variável aleatória com distribuição uniforme no intervalo [2, 5] tem
variância igual a 0, 75.](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-89-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Média e Variância:
E(X) =
a + b
2
e Var(X) =
(b − a)2
12
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
0. V Uma dada variável aleatória com distribuição uniforme no intervalo [2, 5]
tem média igual a 3, 50.](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-90-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Média e Variância:
E(X) =
a + b
2
e Var(X) =
(b − a)2
12
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
0. V Uma dada variável aleatória com distribuição uniforme no intervalo [2, 5]
tem média igual a 3, 50. Temos E(X) = (2 + 5)/2 = 3, 5.](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-91-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Média e Variância:
E(X) =
a + b
2
e Var(X) =
(b − a)2
12
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
0. V Uma dada variável aleatória com distribuição uniforme no intervalo [2, 5]
tem média igual a 3, 50. Temos E(X) = (2 + 5)/2 = 3, 5.
1. V Uma dada variável aleatória com distribuição uniforme no intervalo [2, 5]
tem variância igual a 0, 75.](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-92-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Média e Variância:
E(X) =
a + b
2
e Var(X) =
(b − a)2
12
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
0. V Uma dada variável aleatória com distribuição uniforme no intervalo [2, 5]
tem média igual a 3, 50. Temos E(X) = (2 + 5)/2 = 3, 5.
1. V Uma dada variável aleatória com distribuição uniforme no intervalo [2, 5]
tem variância igual a 0, 75. Temos Var(X) = (5 − 2)2
/12 = 9/12 = 0, 75.](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-93-320.jpg)
![Distribuição Uniforme[a, b]
Função de densidade: X ∼ U[a, b], sua função de densidade é dada por
f(x) =
1
b − a
, a ≤ x ≤ b.
Média e Variância:
E(X) =
a + b
2
e Var(X) =
(b − a)2
12
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
0. V Uma dada variável aleatória com distribuição uniforme no intervalo [2, 5]
tem média igual a 3, 50. Temos E(X) = (2 + 5)/2 = 3, 5.
1. V Uma dada variável aleatória com distribuição uniforme no intervalo [2, 5]
tem variância igual a 0, 75. Temos Var(X) = (5 − 2)2
/12 = 9/12 = 0, 75.](https://image.slidesharecdn.com/anpec2019-1-190613185648/85/Anpec-2019-Estatistica-Questao-1-94-320.jpg)