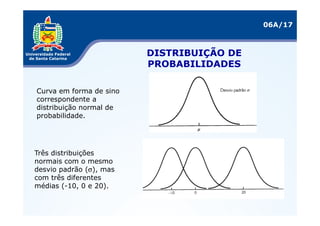
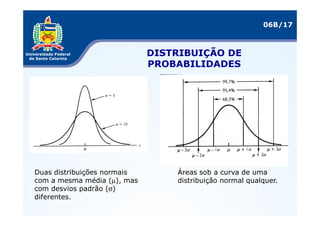
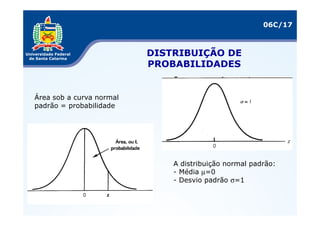
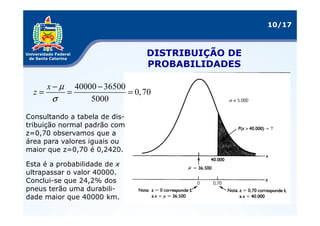
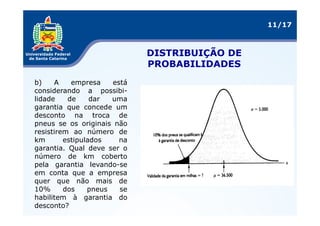
As três distribuições de probabilidade mais comuns são a binomial, normal e uniforme. A distribuição binomial se aplica a variáveis discretas, enquanto a normal é usada para variáveis contínuas. O documento explica como calcular medidas como esperança matemática e variância para essas distribuições e fornece exemplos de sua aplicação em problemas reais.

1. 01/17
DISTRIBUIÇÃO DE
PROBABILIDADES
As distribuições de probabilidades mais conhecidas e utilizadas
na maioria das aplicações são:
-Distribuição binomial - π e n (variável discreta)
-Distribuição normal - µ e σ2 (variável contínua)
Uma função f(x) é quem define o comportamento das
variáveis em termos de resultados de probabilidade
(distribuição).
Função de probabilidade – f(x) – variável discreta
Função densidade de probabilidade – f(x) – variável contínua

2. 02/17
DISTRIBUIÇÃO DE
PROBABILIDADES
Uma diferença fundamental separa as variáveis aleatórias
discretas e as contínuas em termos de como as probabilidades
são calculadas.
Quanto a variável aleatória discreta, f(x) produz a probabili-
dade de a variável aleatória assumir um valor em particular.
Quanto a variável aleatória contínua, f(x) não produz probabili-
dade diretamente; associa a área sob o gráfico de f(x) corres-
pondente a determinado intervalo.
Então, quando se calculam probabilidades de variáveis aleató-
rias contínuas, calcula-se a probabilidade de a variável aleató-
ria assumir qualquer valor nesse intervalo.

3. 03/17
DISTRIBUIÇÃO DE
PROBABILIDADES
FUNÇÃO DE PROBABILIDADE DISCRETA → f(x) ≥ 0
Σf(x) = 1
VALOR ESPERADO DE UMA V.A.D. → E(x)=µ=Σxf(x)
VARIÂNCIA DE UMA V.A.D. → Var(x)=σ2=Σ(x-µ)2f(x)
No. Chamadas Probabilidades No. Chamadas Probabilidades
0 0,10 3 0,20
1 0,15 4 0,15
2 0,30 5 0,10
1) No. esperado de chamadas: E(x)=µ=2,05
2) Variância: σ2=2,05 Desvio Padrão: σ=1,43

4. 04/17
DISTRIBUIÇÃO DE
PROBABILIDADES
DISTRIBUIÇÃO BINOMIAL
VALOR ESPERADO: E(x)=µ=np
VARIÂNCIA: Var(x)=σ2=np(1-p)
Exemplo:
Considere um experimento binomial com n=10 e p=0,10
a) Calcular f(0)= 0,3487
b) Calcular f(2)= 0,1937
c) Calcular P(x≤2)= 0,9298
d) Calcular P(x≥1)= 0,6513
e) Calcular E(x)= 1,0
f) Calcular Var(x)=σ2= 0,9
g) Calcular o desvio padrão - σ= 0,95

5. 05/17
DISTRIBUIÇÃO DE
PROBABILIDADES
Aplicação:
Os sistemas militares de radar e de mísseis são concebidos para um
país precaver-se de ataques inimigos. Uma questão de confiabilidade é
saber se um sistema de detecção será capaz de identificar um ataque
inimigo e disparar um alarme. Considere que determinado sistema de
detecção tenha 90% de probabilidade de detectar um ataque de
mísseis. Use a distribuição binomial para responder as questões a
seguir:
a) Qual a probabilidade de um único sistema de detecção detectar um
ataque? R: 0,90
b) Se dois sistemas são instalados na área e operam independentes,
qual é a probabilidade de pelo menos um deles detectar o ataque? R:
0,99
c) Se três sistemas ... De pelo menos um detectar? R: 0,999
d) Você recomendaria o uso de múltiplos sistemas? R: sim

6. 06/17
DISTRIBUIÇÃO DE
PROBABILIDADES
A DISTRIBUIÇÃO NORMAL DE PROBABILIDADES
1 − ( x − µ ) 2 / 2σ 2
Função Densidade Normal de Probabilidade: f ( x) = e
σ 2π
onde:
µ = média
σ = desvio padrão
π = número pi – 3,141596259
e = 2,7182
1 − z2 / 2
Função Densidade Normal Padrão de Probabilidade: f ( x) = e
2π
Com z = (x - µ)/σ

7. 06A/17
DISTRIBUIÇÃO DE
PROBABILIDADES
Curva em forma de sino
correspondente a
distribuição normal de
probabilidade.
Três distribuições
normais com o mesmo
desvio padrão (σ), mas
com três diferentes
médias (-10, 0 e 20).

8. 06B/17
DISTRIBUIÇÃO DE
PROBABILIDADES
Duas distribuições normais Áreas sob a curva de uma
com a mesma média (µ), mas distribuição normal qualquer.
com desvios padrão (σ)
diferentes.

9. 06C/17
DISTRIBUIÇÃO DE
PROBABILIDADES
Área sob a curva normal
padrão = probabilidade
A distribuição normal padrão:
- Média µ=0
- Desvio padrão σ=1

10. 07/17
DISTRIBUIÇÃO DE
PROBABILIDADES
CARACTERÍSTICAS DA DISTRIBUIÇÃO NORMAL
1. Possui dois parâmetros: a média µ e o desvio padrão σ;
2. Ponto máximo da curva é a média = mediana = moda;
3. A média da distribuição pode ser qualquer valor: negativo, zero ou
positivo;
4. A distribuição normal é simétrica em relação a média;
5. O desvio padrão determina quanto uma curva é achatada ou larga;
6. As probabilidades da va são dadas por área sob a curva; a área
total é igual a 1; como a curva é simétrica, a área, a direita e a
esquerda da média valem 0,5;
7. As porcentagens dos valores de alguns intervalos:
a) 68,3% dos valores de uma va estão dentro de ±1σ da média;
b) 95,4% dos valores de uma va estão dentro de ±2σ da média;
c) 99,7% dos valores de uma va estão dentro de ±3σ da média.

11. 08/17
DISTRIBUIÇÃO DE
PROBABILIDADES
DISTRIBUIÇÃO NORMAL PADRÃO DE PROBABILIDADES
Uma variável aleatória que tem uma distribuição normal com média
igual a zero e desvio padrão igual a um, diz-se que esta variável
tem distribuição normal padrão de probabilidade.
Para encontrar a probabilidade de uma va estar contida em um
intervalo específico, deve-se calcular a área sob a curva normal ao
longo deste intervalo.
Existem tabelas que podem ser usadas para o cálculo das
probabilidades; estas tabelas foram geradas para uma va com
distribuição normal padrão de µ=0 e σ=1

12. 09/17
DISTRIBUIÇÃO DE
PROBABILIDADES
DISTRIBUIÇÃO NORMAL – APLICAÇÃO
Uma empresa desenvolveu um novo pneu radial com cinturão de
aço que será vendido por meio de uma cadeia nacional. Uma vez
que este tipo de pneu é um produto novo, os gerentes da empresa
acreditam que a durabilidade (em termos de km rodados) oferecida
com o pneu será um fator importante na aceitação do produto.
Antes de fechar os termos do contrato de garantia de durabilidade
do pneu, os gerentes desejam obter informações de probabilidade a
respeito do número de km que os pneus durarão. Dos testes reais
de estrada com os pneus, a equipe de engenharia da empresa
estima que a durabilidade média dos pneus é 36500km e que o
desvio padrão é 5000. Além disso, os dados coletados indicam que a
distribuição normal é uma hipótese razoável.
a) Qual percentagem dos pneus duraria mais de 40 mil km? Ou,
qual é a probabilidade de a durabilidade do pneu ultrapassar 40 mil
km?

13. 10/17
DISTRIBUIÇÃO DE
PROBABILIDADES
x−µ 40000 − 36500
z= = = 0, 70
σ 5000
Consultando a tabela de dis-
tribuição normal padrão com
z=0,70 observamos que a
área para valores iguais ou
maior que z=0,70 é 0,2420.
Esta é a probabilidade de x
ultrapassar o valor 40000.
Conclui-se que 24,2% dos
pneus terão uma durabili-
dade maior que 40000 km.

14. 11/17
DISTRIBUIÇÃO DE
PROBABILIDADES
b) A empresa está
considerando a possibi-
lidade de dar uma
garantia que concede um
desconto na troca de
pneus se os originais não
resistirem ao número de
km estipulados na
garantia. Qual deve ser o
número de km coberto
pela garantia levando-se
em conta que a empresa
quer que não mais de
10% dos pneus se
habilitem à garantia do
desconto?

15. 12/17
DISTRIBUIÇÃO DE
PROBABILIDADES
Agora, usando a tabela normal padrão, devemos determinar o valor
de z que produz uma área de 0,10 (10%) sob a curva normal. Este
valor é 1,28; por simetria o valor de z procurado encontra-se a
esquerda da média; z=-1,28.
Para encontrar o valor de x correspondente a z=-1,28 calculamos a
expressão z = x − µ com µ=36500 e σ=5000. Encontra-se x=30100.
σ
Assim, a empresa poderá fixar a garantia de durabilidade de seus
pneus em 30.000km, uma vez que este valor garante que apenas
10% dos pneus produzidos se habilitarão à garantia.

16. 13/17
DISTRIBUIÇÃO DE
PROBABILIDADES
APROXIMAÇÃO NORMAL ÀS PROBABILIDADES BINOMIAIS
Adota-se a aproximação normal às probabilidades binomiais quando
o número de ensaios torna-se grande.
É lícito usar a aproximação quando: a) np ≥ 5; b) n(1-p) ≥ 5.
Ao usar a aproximação normal às probabilidades binomiais ajusta-se
uma curva normal da seguinte maneira:
µ = np e σ2 = np(1-p)
A distribuição normal trabalha com va contínua e a probabilidade é
obtida a partir da área sob a curva normal. A distribuição binomial
trabalha com va discreta e a probabilidade é obtida para cada valor
assumido por x.
Truque: P(x=12) da binomial é igual a P(11,5 ≤ x ≤ 12,5) da normal.

17. 14/17
DISTRIBUIÇÃO DE
PROBABILIDADES
EXERCÍCIOS