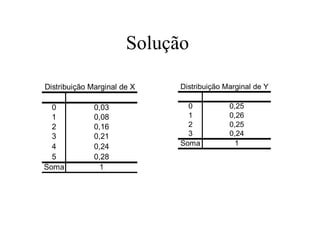
1) Uma variável aleatória é uma função que associa valores numéricos a resultados de um experimento aleatório. 2) Existem variáveis aleatórias discretas, onde os resultados possíveis estão em um conjunto finito ou enumerável, e variáveis aleatórias contínuas, onde os resultados podem assumir qualquer valor numérico em um intervalo. 3) As distribuições de probabilidade de variáveis aleatórias discretas são representadas por funções de probabilidade, enquanto variáveis aleatórias contínuas usam funções

1. VARIÁVEL ALEATÓRIA
• Definição: Seja (Ε) um experimento
aleatório e seja (S) um espaço amostral
associado ao experimento. Uma função
de X, que associe a cada elemento s
∈ S um número real x(s), é denominada
variável aleatória.
X
s x(s)
S X(S)

2. Exemplos de Variáveis aleatórias
• Número obtido no lançamento de um dado;
• Número de caras obtido no lançamento de duas moedas;
• Número de itens defeituosos em uma amostra retirada,
aleatoriamente, de um lote;
• Número de defeitos em um azulejo que sai da linha de
produção;
• Número de pessoas que visitam um determinado site, num
certo período de tempo;
• Volume de água perdida por dia, num sistema de
abastecimento;
• Resistência ao desgaste de um tipo de aço, num teste padrão;
• Tempo de resposta de um sistema computacional;
• Grau de empeno em um azulejo que sai da linha de produção.

3. Exemplo 1
• Suponha que lançamos duas moedas.
Definimos uma variável aleatória como
sendo o número de caras obtido nas duas
moedas.
– Encontre o espaço amostral
– Calcule as probabilidades da v.a.

4. Solução
• Espaço amostral
S = { ( coroa, coroa ) , ( coroa, cara ) , ( cara, coroa ) , ( cara, cara )}
0 1 2 x
X = número de caras = { 0,1, 2}
• As probabilidades:
1 1 1
P( X = 0 ) = P (coroa, coroa) = * =
2 2 4
1 1 1 1 2
P( X = 1) = P{ ( coroa, car ) , ( cara, coroa )} = * + * =
2 2 2 2 4
1 1 1
P( X = 2 ) = P( cara, cara ) = * =
2 2 4

5. Variáveis Aleatórias Discretas
• Variável aleatória discreta
– Os possíveis resultados estão contidos em um
conjunto finito ou enumerável
– Exemplos:
• Número de caras obtido no lançamento de duas moedas;
• Número de itens defeituosos em uma amostra retirada,
aleatoriamente, de um lote;
• Número de defeitos em um azulejo que sai da linha de
produção;
• Número de pessoas que visitam um determinado site, num
certo período de tempo;

6. FUNÇÃO DE PROBABILIDADE OU
DISTRIBUIÇÃO DE PROBABILIDADE
• Se X for uma V.A. discreta, com os
possíveis valores { x1 , x2 , , xn , }, então a
distribuição de probabilidade de X pode ser
apresentada pela chamada função de
probabilidade, que associa a cada valor
possível x i a sua probabilidade de ocorrência
P ( xi ) , ou seja:
P( X = xi ) = P( xi ) = p i
• Uma função de probabilidade deve
satisfazer i) 0 ≤ P( x ) ≤1
i
∞
ii ) ∑P ( x i ) =1
i=1

7. Exemplo 2
• Seja X a variável aleatória que indica o
número de caras no lançamento de 3
moedas. Apresente a distribuição de X em
uma tabela.

8. Solução
{
S = ( coroa, coroa, coroa ) , ( coroa, coroa, cara ) , ( coroa, cara, coroa ) , ( cara, coroa, coroa ) ,
( cara, cara, coroa ) , ( cara, coroa, cara ) , ( coroa, cara, cara ) , ( cara, cara, cara ) }
X = número de caras = { 0,1, 2,3}
1 1 1 1
P( X = 0 ) = P(coroa, coroa, coroa) = * * =
2 2 2 8
1 1 1 3
P( X = 1) = P{ ( coroa, coroa, cara ) , ( coroa, cara, coroa ) , ( cara, coroa, coroa )} = 3 * * * =
2 2 2 8
1 1 1 3
P( X = 2 ) = P{ ( cara, cara, coroa ) , ( cara, coroa, cara ) , ( coroa, cara, cara )} = 3 * * * =
2 2 2 8
1 1 1 1
P( X = 3) = P( cara, cara, cara ) = * * =
2 2 2 8
X P(X=x)
0 1/8
1 3/8
2 3/8
3 1/8

9. Função de distribuição acumulada
• Outra forma de representar uma distribuição
de probabilidades de uma variável aleatória é
através de distribuição acumulada, que é
definida por:
F ( x) = P ( X ≤ x), ∀x ∈ ℜ,
ℜ é conjunto onde a variável aleatória está
definida

10. Exemplo 3
• Seja a variável aleatória do exemplo 2,
encontre a função de distribuição
acumulada.
X P(X=x)
0 1/8
1 3/8
2 3/8
3 1/8

11. Solução
0 se x<0
 18
 se 0 ≤ x <1
F ( x ) = 4 8 se 1≤ x < 2
7 8 se 2≤ x<3
1
 se x≥3
F(x)
1
⅞
⅝
⅜
⅛
0 1 2 3 x

12. Variáveis Aleatórias Contínuas
• Variável aleatória contínua
– Os possíveis resultados abrangem todo um intervalo de números reais
– Exemplos:
• Volume de água perdida por dia, num sistema de abastecimento;
• Resistência ao desgaste de um tipo de aço, num teste padrão;
• Tempo de resposta de um sistema computacional;
• Grau de empeno em um azulejo que sai da linha de produção.
Obs:
Há variáveis aleatórias discretas, com grande número de
possíveis resultados, em que é preferível usar um modelo
aproximado contínuo no lugar de um modelo exato discreto:
– Número de transações por segundo de uma CPU
– Número de defeitos numa amostra de 5000 itens

13. FUNÇÃO DENSIDADE DE
PROBAILIDADE
• As probabilidades de eventos associados a
uma variável aleatória contínua X podem ser
calculadas através de uma função densidade
de probabilidade f, que deve satisfazer:
i ) f ( x ) ≥ 0, ∀x ∈ℜ
+∞
ii ) ∫ f ( x) dx =1 f(x)
−∞
Se A = [a, b], então P( A) = ∫ f ( x)dx
b
a
a b x

14. Exemplo 4
• Seja a variável aleatória T definida como o
tempo de resposta na consulta a um banco
de dados, em minutos. Suponha que essa
variável aleatória tenha a seguinte função
densidade de probabilidade:
2e −2 t ,
f (t) =  para t ≥ 0
0, para t < 0
Calcular a probabilidade de a resposta
demorar mais do que 3 minutos.

15. Solução
∞
( t ≥ 3) = ∫ f ( t ) dt = ∫ 2e − 2t dt = 2− 1 e − 2t  = 0 + e − 2 (3) = e −6 = 0,0025
∞ ∞
P  2 
3 3  3

16. FUNÇÃO DE DISTRIBUIÇÃO
ACUMULADA
• Como X é uma variável aleatória contínua
com função de densidade de probabilidade
f, definimos sua função de distribuição
acumulada por:
x
F ( x) = P ( X ≤ x) = ∫ f ( s )ds, ∀x ∈ ℜ
−∞
OBS: dF ( x )
= f ( x)
dx

17. Exemplo 5
• Considere a função densidade de probabilidade
do exemplo 4 e obtenha a função de
distribuição acumulada.
2e −2 t ,
f (t) =  para t ≥ 0
0, para t < 0

18. Solução
t t
Para t < 0 ⇒ F ( t ) = ∫ f ( s ) ds = ∫ 0dt = 0
−∞ −∞
f ( s ) ds = ∫ 0ds + ∫ 2e −2 s ds = 0 + [ − e −2 s ] 0 = 1 − e −2 t
t 0 t
Para t ≥ 0 ⇒ F ( t ) =
t
∫
−∞ −∞ 0
Resumindo, a função de distribuição
acumulada da variável aleatória T é dada por:
1 − e −2 t , para t ≥ 0
F(t) = 
0, para t < 0

19. Variáveis Aleatórias Bidimensionais
• Definição
– Seja E um experimento e S um espaço amostral
associado a E. Sejam X = X ( s ) e Y = Y ( s ) duas
funções, cada uma associando um número real
a cada resultado s ∈ S . Denotaremos (X, Y) uma
v. a. bidimensional.
S X(s)
X
s
Y Y(s)

20. Variável Aleatória Discreta
Bidimensional
• (X, Y) será uma v.a. discreta bidimensional
se os valores possíveis de (X, Y) forem
finitos ou infinitos numeráveis, isto é, os
valores possíveis de (X, Y) possam ser
representados por ( x , y ), i = 1,2, , n,  ; j = 1, 2,  , m., 
i j

21. Função de Probabilidade ou
Distribuição de Probabilidade de (X, Y)
• Seja (X, Y) uma v.a. discreta bidimensional. A
cada resultado possível( x , y ) associaremos um
i j
número p( x , y ) representando P( X = x , Y = y ) e
i j i j
satisfazendo as seguintes condições:
a ) p ( xi , y j ) ≥ 0
b) ∑∑ p ( xi , y j ) =1
∞ ∞
i=1 j=1

22. Exemplo 6
• Duas linhas de produção fabricam um certo tipo de peça. Suponha que a
capacidade (em qualquer dia) seja 5 peças na linha I e 3 peças na linha II.
Admita que o número de peças realmente produzidas em qualquer linha seja
uma v.a. e que (X, Y) represente a v.a. bidimensional que fornece o número de
peças produzidas pela linha I e a linha II, respectivamente. A tabela 1 dá a
distribuição de probabilidade conjunta de (X, Y)
Tabela 1: Distribução de probabilidade conjunto de (X, Y)
X 0 1 2 3 4 5 Soma
Y
0 0 0,01 0,03 0,05 0,07 0,09 0,25
1 0,01 0,02 0,04 0,05 0,06 0,08 0,26
2 0,01 0,03 0,05 0,05 0,05 0,06 0,25
3 0,01 0,02 0,04 0,06 0,06 0,05 0,24
0,03 0,08 0,16 0,21 0,24 0,28 1
( ) (
Cada casa representa p xi , y j = P X = xi , Y = y j )
Se B = {mais peças são produzidas pela linha I que pela linha II}, calcule P(B)

23. Solução
P( B ) = p(1,0) + p (2,0) + p(2,1) + p(3,0) + p(3,1) + p(3,2) + p(4,0) +
p(4,1) + p(4,2) + p(4,3) + p(5,0) + p(5,1) + p(5,2) + p(5,3) =
0,01 + 0,03 + 0,04 + 0,05 + 0,05 + 0,05 + 0,07 + 0,06 + 0,05 +
0,06 + 0,09 + 0,08 + 0,06 + 0,05
P( B ) = 0,75

24. Variável Aleatória Contínua
Bidimensional
• (X, Y) será uma v.a. contínua bidimensional
se (X, Y) puder assumir todos os valores em
algum conjunto não-numerável do plano
euclidiano.
• Se (X, Y) assumir todos os valores no
retângulo{ ( x, y ) | a ≤ x ≤ b, c ≤ y ≤ d } ou todos os
valores no circulo { ( x, y ) | x + y ≤ 1} ,
2 2
poderemos dizer que (X, Y) é uma v.a.
bidimensional contínua.

25. Função Densidade de Probabilidade
Conjunta
• Seja (X, Y) uma v.a. contínua
assumindo todos os valores em uma
região ℜ do plano euclidiano. A função
densidade de probabilidade conjunta f é
uma função que satisfaz as seguintes
condições:
a ) f ( x, y ) ≥ 0 para todo ( x, y ) ∈ ℜ
b) ∫∫ f ( x, y ) dxdy = 1
ℜ

26. Exemplo 7
• Suponha que um fabricante de lâmpadas esteja
interessado no número de lâmpadas
encomendadas a ele durante os meses de
janeiro e fevereiro. Sejam X e Y,
respectivamente, o número de lâmpadas
encomendadas durante esses dois meses.
Admitiremos que (X, Y) seja uma v.a. contínua
bidimensional com a seguinte fdp conjunta
{
f ( x, y ) = c, se 5000 ≤ x ≤ 10000 e 4000 ≤ y ≤ 9000
0, nos demais casos
Se B = { X ≥ Y} , calcule P(B)

27. Solução
• Determinar c
+∞ +∞ 9000 10000
1
∫∫ f ( x, y )dxdy = 1 ⇒ ∫ ∫ cdxdy = 1 ⇒ 5000 c = 1 ⇒ c =
2
= 5000 −2
−∞ −∞ 4000 5000 5000 2
• Calculo de P(B)
Y=X
9000
4000
5000 10000
1
10000 x
1 1 10000
P( B ) = ∫ ∫ dydx = 2 ∫
y |4000 dx =
x
2 ∫
( x − 4000) dx = 0,7
5000 4000 5000 5000 5000 5000
2

28. Exercício 1
• Calcular a probabilidade de B usando o
seguinte artifício:
( )
P( B ) = 1 − P B

29. Função de Distribuição Acumulada
• Seja (X, Y) uma v.a. bidimensional. A
função de distribuição acumulada F(x)
da v.a. (X, Y) é definida como:
F ( x, y ) = P ( X ≤ x, Y ≤ y )
OBS: ∂2 F ( x, y )
= f ( x, y )
∂x∂y

30. Distribuição de Probabilidade
Marginal
• Caso Discreto: Seja (X, Y) uma v.a. discreta
bidimensional.
– A distribuição marginal de X:
∞
p( xi ) = P( X = xi ) = P( X = xi , Y = y1 ou X = xi , Y = y2 ou ) = ∑ p( xi , y j )
j =1
– A distribuição marginal de Y:
∞
q( y j ) = P (Y = y j ) = ∑ p ( xi , y j )
i =1

31. Exemplo 8
• Represente em forma de tabela as funções
marginal de X e Y do exemplo 6.
Tabela 1: Distribução de probabilidade conjunto de (X, Y)
X 0 1 2 3 4 5 Soma
Y
0 0 0,01 0,03 0,05 0,07 0,09 0,25
1 0,01 0,02 0,04 0,05 0,06 0,08 0,26
2 0,01 0,03 0,05 0,05 0,05 0,06 0,25
3 0,01 0,02 0,04 0,06 0,06 0,05 0,24
0,03 0,08 0,16 0,21 0,24 0,28 1

32. Solução
Distribuição Marginal de X Distribuição Marginal de Y
0 0,03 0 0,25
1 0,08 1 0,26
2 0,16 2 0,25
3 0,21 3 0,24
4 0,24 Soma 1
5 0,28
Soma 1

33. Distribuição de Probabilidade
Marginal
• Caso Contínuo:
– Função densidade de probabilidade marginal de X
∞
g ( x ) = ∫ f ( x, y ) dy
−∞
– Função densidade de probabilidade marginal de Y
∞
h( y ) = ∫ f ( x, y ) dx
−∞

34. Exemplo 9
• Suponha-se que (X, Y) seja uma v.a.
contínua bidimensional com fdp conjunta
{
f ( x, y ) = 2( x + y − 2 xy ) , 0 ≤ x ≤ 1 e 0 ≤ y ≤ 1
0, para quaisquer outros valores
Encontre g ( x ) e h( y )

35. Solução
• A função marginal de X:
1 1
g ( x ) = ∫ f ( x, y ) dy = ∫ 2( x + y − 2 xy ) dy = 1, então
0 0
g ( x ) = 1, 0 ≤ x ≤ 1
• A função marginal de Y:
1 1
h( y ) = ∫ f ( x, y ) dx = ∫ 2( x + y − 2 xy ) dx = 1, então
0 0
h( y ) = 1, 0 ≤ y ≤ 1

36. Distribuição de Probabilidade
Condicionada
• Caso Discreto:
p ( xi , y j )
p ( xi y j ) = P ( X = xi Y = y j ) = , q( y j ) > 0
q( y j )
p ( xi , y j )
q ( y j xi ) = P ( Y = y j X = xi ) = , p ( xi ) > 0
p ( xi )

37. Exemplo 10
• Consideremos o exemplo 6 da linha de
produção I e II. Suponhamos que se deseja
calcular as seguintes probabilidades
condicionada:
P( X = 2 Y = 2) e P( Y = 2 X = 2)
Tabela 1: Distribução de probabilidade conjunto de (X, Y)
X 0 1 2 3 4 5 Soma
Y
0 0 0,01 0,03 0,05 0,07 0,09 0,25
1 0,01 0,02 0,04 0,05 0,06 0,08 0,26
2 0,01 0,03 0,05 0,05 0,05 0,06 0,25
3 0,01 0,02 0,04 0,06 0,06 0,05 0,24
0,03 0,08 0,16 0,21 0,24 0,28 1

38. Solução
p( 2,2) P( X = 2, Y = 2) 0,05
P( X = 2 Y = 2) = = = = 0,2
q( 2) Q(Y = 2) 0,25
p (2,2) P ( X = 2, Y = 2 ) 0,02
P( Y = 2 X = 2) = = = = 0,125
p ( 2) P( X = 2) 0,16

39. Distribuição de Probabilidade
Condicionada
• Caso Contínuo:
f ( x, y )
g( x y) = , h( y ) > 0
h( y )
f ( x, y )
h( y x ) = , g ( x) > 0
g ( x)

40. Exemplo 11
• Suponha-se que (X, Y) seja uma v.a.
contínua bidimensional tenha uma fdp
conjunta dada por:
 2 xy

f ( x, y ) =  x + 3 , 0 ≤ x ≤1 e 0 ≤ y ≤ 2
0,
 caso contrário
Calcular as probabilidades condicionada
g ( x y ) e h( y x )

41. Solução
• Como f ( x, y ) f ( x, y )
g( x y) = e h( y x ) =
h( y ) g ( x)
• Temos que calcular g ( x ) e h( y )
1 1
 xy  1 1
h( y ) = ∫ f ( x, y ) dy = ∫  x 2 + dx = + y 0≤ y≤2
0 0  3 3 6
2 2
 2 xy  2
g ( x ) = ∫ f ( x, y ) dy = ∫  x + dy = 2 x + x
2
0 ≤ x ≤1
0 0  3 3
f ( x, y ) x 2 + xy 3 ( 3 x 2 + xy ) 3 6 x 2 + 2 xy
g( x y) = = = = , 0 ≤ x ≤ 1, 0 ≤ y ≤ 2
h( y ) 1 3+ y 6 ( 2 + y) 6 2+ y
f ( x, y ) x + xy 3 3x + y
2
h( y x ) = = 2 = , 0 ≤ x ≤ 1, 0 ≤ y ≤ 2
g ( x) 2x + 2x 3 6x + 2

42. Variáveis Aleatórias Independentes
• Caso Discreto
– Se (X, Y) é uma v.a. discreta bidimensional. Diremos
que X e Y são v.a.’s independentes se, e somente se,
p( x , y ) = p( x ) q( y )
i j i j
i, j para quaisquer
P (.X = x ,é, = y ) = P( X = x ) Q(Y = y )
Isto Y i j i
i, j
para todo .

43. Exemplo 12
• Mostre que X e Y da v.a. bidimensional do
exemplo 6 são independentes.
Tabela 1: Distribução de probabilidade conjunto de (X, Y)
X 0 1 2 3 4 5 Soma
Y
0 0 0,01 0,03 0,05 0,07 0,09 0,25
1 0,01 0,02 0,04 0,05 0,06 0,08 0,26
2 0,01 0,03 0,05 0,05 0,05 0,06 0,25
3 0,01 0,02 0,04 0,06 0,06 0,05 0,24
0,03 0,08 0,16 0,21 0,24 0,28 1

44. Solução
• Para que X e Y sejam independentes,
temos:
p ( x , y ) = p( x ) q ( y ) ou P ( X = x , Y = y ) = P( X = x ) Q(Y = y )
i j i j i j i
• Da tabela temos:
P( X = 0, Y = 0 ) = P( X = 0) Q( Y = 0) , ou seja
0 ≠ 0,03 * 0,25, então X e Y não são independentes

45. Variáveis Aleatórias Independentes
• Caso Contínuo:
– Se (X, Y) é uma v.a. contínua bidimensional.
Diremos que X e Y são v.a.’s independentes se,
e somente se, f ( x, y ) = g ( x ) * h( y ) para todo ( x, y ),
onde f ( x, y ) é a fdp conjunta e g ( x ) e h( y ) são
as fdp’s marginais de X e Y, respectivamente.

46. Exemplo 13
• Seja X e Y a duração da vida de dois
dispositivos eletrônicos. Suponha-se que
sua fdp conjunta seja dada por:
f ( x, y ) = e − ( x+ y )
, x ≥ 0, y ≥ 0
Mostre que x e Y são independentes.

47. Solução
Como:
f ( x, y ) = e − ( x + y ) = e − x − y = e − x * e − y = g ( x ) * h ( y )
Então X e Y são independentes