1) O documento discute modelos probabilísticos discretos, incluindo variáveis aleatórias discretas e suas distribuições de probabilidade.
2) É introduzido o modelo uniforme para descrever experimentos como lançamento de dados, onde cada resultado tem a mesma probabilidade.
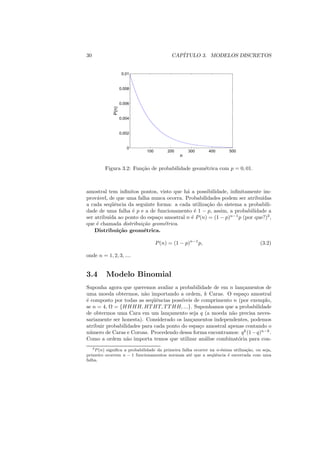
3) O modelo geométrico é usado para descrever o intervalo até a primeira falha em sistemas, como de aterrissagem de aviões, onde a probabilidade de falha é constante a cada uso.