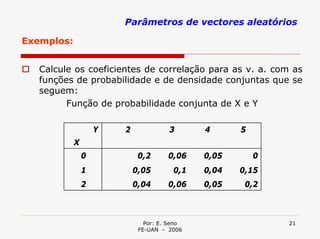
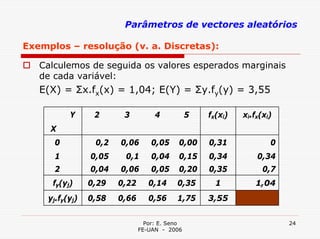
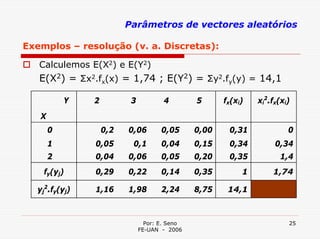
Este documento resume as principais características de variáveis aleatórias, incluindo valor esperado, variância, covariância e coeficiente de correlação. O valor esperado é a média da distribuição de probabilidade da variável aleatória. A variância mede a dispersão em torno do valor esperado. A covariância mede a associação entre duas variáveis e o coeficiente de correlação mede essa associação de forma relativa.

1. Material para os estudantes do 2.º ano
CARACTERÍSTICAS DE
VARIÁVEIS ALEATÓRIAS
Por: E. Seno 1
FE-UAN - 2006

2. Características (Medidas) das v. a.
Valor esperado = Esperança matemática
(média)
Variância, Desvio-padrão e Coeficiente de
variação
Covariância
Coeficiente de Correlação
Por: E. Seno 2
FE-UAN - 2006

3. Valor esperado
Definição:
Centro de gravidade da distribuição de probabilidade
da variável aleatória
Matematicamente:
• Para variável discreta:
N
E ( X ) = µ x = ∑ xi . f ( xi )
i =1
• Para variável contínua:
+∞
E( X ) = µx = ∫ x. f ( x)dx
−∞
Por: E. Seno 3
FE-UAN - 2006

4. Valor esperado
Exemplo – v. a. d.:
No caso do lançamento de uma moeda três vezes, pode-
se calcular o número esperado de faces, da seguinte
forma:
N 4
E ( x) = ∑ xi . f ( xi ) =∑ xi . f ( xi ) =
i =1 i =1
= 0 × 0,125 + 1× 0,375 + 2 × 0,375 + 3 × 0,125 =
= 0 + 0,375 + 0,75 + 0,375 = 1,5.
Ou, seja:
x 0 1 2 3 ∑
f(x) = 0,125 0,375 0,375 0,125 1
x.f(x) 0 0,375 0,75 0,375 1,5
Por: E. Seno 4
FE-UAN - 2006

5. Valor esperado
Exemplo – v. a. c.: :
No caso da variável a. contínua, calculamos o valor
esperado da variável cuja função de densidade é
dada por:
⎧ 0
⎪x
; x< 0
f ( x) = ⎨ + 1 ; 0≤ x≤3
⎪ 018
⎩
4
; x >3
Da seguinte forma:
+∞
⎛ x 1⎞
3
E ( x) =
−
∫∞ x. f ( x ) dx = ∫ x × ⎜ + ⎟ dx =
0 ⎝ 18 4 ⎠
3
⎡1 x 1 x ⎤3
⎡ 1 33 1 3 2 ⎤
2
⎢ × + × ⎥ = ⎢ × + × ⎥ − 0 = 1,625 .
⎣18 3 4 2 ⎦ 0 ⎣18 3 4 2 ⎦
Por: E. Seno 5
FE-UAN - 2006

6. Valor esperado
Propriedades:
1. E(a) = a
N N
E (a ) = ∑ af ( xi ) = a ∑ f (xi ) = a.1 = a,
i =1 i =1
ou ,
+∞ +∞
E (a ) = ∫ af ( x)dx = a ∫ f ( x)dx = a.1 = a
−∞ −∞
Por: E. Seno 6
FE-UAN - 2006

7. Valor esperado
Propriedades:
2. E(X+Y) = E(X) + E(Y)
(Podemos demonstrar para o caso de uma v. a.
Discreta)
M N M N
E ( X + Y ) = ∑∑ ( xi + y j ) f ( xi , y j ) =∑∑ xi f ( xi , y j ) +
i= j =1 i= j =1
M N M N N M
+ ∑∑ y j f ( xi , y j ) = ∑ xi ∑ f ( xi , y j ) + ∑ y j ∑ f ( xi , y j ) =
i =1 j =1 i =1 j =1 j =1 i =1
M N
= ∑ xi f x ( xi ) + ∑ y j f y ( y j ) = E ( X ) + E (Y )
i =1 j =1
Por: E. Seno 7
FE-UAN - 2006

8. Valor esperado
Propriedades:
3. E(a + bX) = E(a) + bE(X) = a + bE(X)
4. Valor esperado conjunto:
M N
E ( X , Y ) = ∑∑ ( xi , y j ) f ( xi , y j ), para v. a. discreta
i= j =1
ou ,
+ ∞+ ∞
E( X ,Y ) = ∫ ∫ xyf ( x, y)dxdy,
− ∞− ∞
para v. a. contínua
Por: E. Seno 8
FE-UAN - 2006

9. Valor esperado
Propriedades:
5. Valor esperado conjunto de variáveis aleatórias
independentes: E(XY) = E(X).E(Y)
M N M N
E(X,Y) = ∑ ∑ (x i ,y j )f(x i ,y j ) = ∑ ∑ xi .y j f x(x i )f y (y j ) =
i= j =1 i= j =1
M N
= ∑ xi f x(x i ).∑ y j f y (y j ) = E(X).E(Y) , para v. a. discreta
i =1 j =1
ou ,
+ ∞+ ∞ + ∞+ ∞
E ( X ,Y ) = ∫ ∫ xyf ( x , y ) dxdy = ∫ ∫ xyf
− ∞− ∞ − ∞− ∞
x ( x ). f y ( y ) dxdy =
+∞ +∞
= ∫ xf
−∞
x ( x ) dx . ∫ yf y ( y ) dy = E ( X ). E (Y ), para v. a. contínua
−∞
Por: E. Seno 9
FE-UAN - 2006

10. Valor esperado
Propriedades:
6. Valor esperado de uma soma de v. a. iid (independentes
e identicamente distribuídas), isto é E(X1) = E(X2) = …
= E(XN) e V(X1) = V(X2) = … = V(XN)
E ( X 1 + X 2 + ... + X N ) = E ( X 1 ) + E ( X 2 ) + ... + E ( X N ) =
64444vezes 444
N
74 8
= E ( X ) + E ( X ) + ... + E ( X ) = N .E ( X )
Por: E. Seno 10
FE-UAN - 2006

11. Valor esperado
Propriedades:
7. Valor esperado condicionado
De X dado Y :
M M f(x i ,y j )
E(XY) = ∑x
i =1
i f(x iy j ) = ∑x
i =1
i
f y (y j )
, ou
+∞ +∞
f(x,y)
E(XY) = ∫
−∞
xf(xy)dx = ∫
−∞
x
f y (y)
dx
De Y dado X :
N N f(x i ,y j )
E(YX) = ∑
j =1
y j f(y jx i ) = ∑j =1
yj
f x (x i )
, ou
+∞ +∞
f(x,y)
E(YX) = ∫
−∞
yf(yx)dy = ∫
−∞
y
f x (x)
dy
Por: E. Seno 11
FE-UAN - 2006

12. Variância
Definição:
Valor esperado do quadrado do desvio entre a variável e
o seu valor esperado, ou seja:
σ2 = V(X) = E[X – E(X)]2 = E(X2) – E2(X)
Onde:
N
E ( X ) = ∑ x i . f ( xi ) ;
2 2
para variáveis discretas,
i =1
ou,
+∞
E(X 2 ) = ∫
−∞
x 2 . f ( x)dx ; para variáveis contínuas
E, E2(X) = [E(X)]2
Por: E. Seno 12
FE-UAN - 2006

13. Variância
Exemplo – v. a. d.:
No caso do lançamento de uma moeda três vezes, pode-
se calcular a variância do número esperado de faces, da
seguinte forma:
N 4
E (x ) = ∑ xi . f ( xi ) = ∑ xi . f ( xi ) =
2 2 2
i =1 i =1
= 0 2 × 0 ,125 + 1 2 × 0 , 375 + 2 2 × 0 , 375 + 3 2 × 0 ,125 =
= 0 + 0 , 375 + 1, 5 + 1,125 = 3 .
σ 2
= V ( X ) = E ( X 2 ) − E 2 ( X ) = 3 − (1, 5 ) 2 = 0 , 75 .
σ = σ 2
= 0 , 75 = 0 , 866 .
σ 0 , 866
Cv = = = 0 , 57735 = 57 , 7 %.
E(X ) 1, 5
Por: E. Seno 13
FE-UAN - 2006

14. Variância
Exemplo – v. a. c.:
Voltando ao exemplo anterior:
+∞
⎛ x 1⎞
3
E ( x ) = ∫ x . f ( x ) dx = ∫ x × ⎜ + ⎟ dx =
2 2 2
−∞ 0 ⎝ 18 4 ⎠
3
⎡ 1 x4 1 x3 ⎤ ⎡ 1 3 4 1 33 ⎤
⎢ × + × ⎥ = ⎢ × + × ⎥ − 0 = 3,375 .
⎣18 4 4 3 ⎦ 0 ⎣18 4 4 3 ⎦
σ 2 = V ( X ) = E ( x 2 ) − E 2 ( X ) = 3,375 − (1,625 ) 2 = 0,73438 .
σ = σ 2 = 0,73438 = 0 .85696 .
σ 0,85696
Cv = = = 0,52736 = 52 ,7 %
E(X ) 1,625
Por: E. Seno 14
FE-UAN - 2006

15. Variância
Propriedades:
1. V(X) ≥ 0
2. V(a) = 0
V(a) = E[a – E(a)]2 = E(a – a)2 = E(0) = 0.
3. V(b.X) = E[bX – E(bX)]2 = E[bX – bE(X)]2 =
= E{b[X – E(X)]}2 = E{b2.[X – E(X)]2} =
= b2.E[X – E(X)]2 = b2.V(X)
Por: E. Seno 15
FE-UAN - 2006

16. Variância
Propriedades:
4. V(X ± Y) = V(X) + V(Y) ± 2.Cov(XY)
V ( X ± Y ) = E [( X ± Y ) − E ( X ± Y )] = E [X − E ( X ) ± Y m E (Y )] =
2 2
E{[X − E ( X )] ± [Y − E (Y )]} = E [X − E ( X )] + E [Y − E (Y )] ±
2 2 2
± 2 E [X − E ( X )][Y − E (Y )] = V ( X ) + V (Y ) ±
.
± 2[E ( XY ) − E ( X ) E (Y ) − E ( X ) E (Y ) + E ( X ) E (Y )] =
= V ( X ) + V (Y ) ± 2[E ( XY ) − E ( X ) E (Y )]
1444 444 2 3
Cov xy
Por: E. Seno 16
FE-UAN - 2006

17. Variância
Propriedades:
5. V(X ± Y) = V(X) + V(Y), se X e Y independentes, porque
neste caso:
E(XY) = E(X)E(Y).
6. V(a + bX) = b2.V(X)
7. Variância de uma soma de v. a. iid (independentes e
identicamente distribuídas):
V ( X 1 + X 2 + ... + X N ) = V ( X 1 ) + V ( X 2 ) + ... + V ( X N ) =
6444 N74444 4vezes 8
= V ( X ) + V ( X ) + ... + V ( X ) = N .V ( X )
Por: E. Seno 17
FE-UAN - 2006

18. Covariância
Definição:
Medida de associação entre as variáveis (em termos
absolutos)
Covxy = E(XY) – E(X)E(Y)
Logo, se X e Y são independentes ⇒ Covxy =0.
Mas o contrário nem sempre é verdade
Se Covxy > 0 ⇒ Relação directa entre as variáveis,
evoluem no mesmo sentido;
Se Covxy < 0 ⇒ Relação inversa entre as variáveis,
evoluem em sentidos opostos. Se uma aumenta,
outra diminui e vice-versa.
Por: E. Seno 18
FE-UAN - 2006

19. Coeficiente de correlação
Definição:
Medida de associação entre as variáveis (em termos
relativos)
E [ X − E ( X ) ][Y − E ( Y ) ] Cov
r xy = =
xy
E [ X − E ( X ) ] . E [Y − E ( Y ) ] σ xσ
2 2
y
|rxy| ≤ 1;
Logo, se X e Y são independentes ⇒ rxy = 0.
Mas o contrário nem sempre é verdade
Em relação ao sinal, avalia-se o sentido da relação;
Em relação à grandeza do valor, avalia-se a força da
relação.
Por: E. Seno 19
FE-UAN - 2006

20. Coeficiente de correlação
Definição – cont.:
Em relação ao sinal:
Se rxy > 0 ⇒ relação directa;
Se rxy < 0 ⇒ relação inversa.
Em relação à grandeza:
Se 0 < |rxy| ≤ 0,5 ⇒ relação fraca;
Se 0,5 < |rxy| < 1 ⇒ relação forte;
Se |rxy| = 1 ⇒ correlação total.
Por: E. Seno 20
FE-UAN - 2006

21. Parâmetros de vectores aleatórios
Exemplos:
Calcule os coeficientes de correlação para as v. a. com as
funções de probabilidade e de densidade conjuntas que se
seguem:
Função de probabilidade conjunta de X e Y
Y 2 3 4 5
X
0 0,2 0,06 0,05 0
1 0,05 0,1 0,04 0,15
2 0,04 0,06 0,05 0,2
Por: E. Seno 21
FE-UAN - 2006

22. Parâmetros de vectores aleatórios
Exemplos:
Função de densidade conjunta de X e Y
⎧
⎪
1
, -
1
≤ x≤
1
; -
1
≤ y≤
1
f ( x, y ) = ⎨2 2 2 2 2
⎪0
⎩ caso contrário
Por: E. Seno 22
FE-UAN - 2006

23. Parâmetros de vectores aleatórios
Exemplos – resolução (v. a. Discretas):
Comecemos por determinar o valor esperado conjunto
E(XY) = ΣΣxy.f(x,y) = 4,23
Y 2 3 4 5 Σ
X
0 0 0 0 0 0
1 0,1 0,3 0,16 0,75 1,31
2 0,16 0,36 0,4 2 2,92
Σ 0,26 0,66 0,56 2,75 4,23
Por: E. Seno 23
FE-UAN - 2006

24. Parâmetros de vectores aleatórios
Exemplos – resolução (v. a. Discretas):
Calculemos de seguida os valores esperados marginais
de cada variável:
E(X) = Σx.fx(x) = 1,04; E(Y) = Σy.fy(y) = 3,55
Y 2 3 4 5 fx(xi) xi.fx(xi)
X
0 0,2 0,06 0,05 0,00 0,31 0
1 0,05 0,1 0,04 0,15 0,34 0,34
2 0,04 0,06 0,05 0,20 0,35 0,7
fy(yj) 0,29 0,22 0,14 0,35 1 1,04
yj.fy(yj) 0,58 0,66 0,56 1,75 3,55
Por: E. Seno 24
FE-UAN - 2006

25. Parâmetros de vectores aleatórios
Exemplos – resolução (v. a. Discretas):
Calculemos E(X2) e E(Y2)
E(X2) = Σx2.fx(x) = 1,74 ; E(Y2) = Σy2.fy(y) = 14,1
Y 2 3 4 5 fx(xi) xi2.fx(xi)
X
0 0,2 0,06 0,05 0,00 0,31 0
1 0,05 0,1 0,04 0,15 0,34 0,34
2 0,04 0,06 0,05 0,20 0,35 1,4
fy(yj) 0,29 0,22 0,14 0,35 1 1,74
yj2.fy(yj) 1,16 1,98 2,24 8,75 14,1
Por: E. Seno 25
FE-UAN - 2006

26. Parâmetros de vectores aleatórios
Exemplos – resolução (v. a. Discretas):
Cálculo da covariância:
Covxy = E(XY) – E(X).E(Y) = 4,23 – 1,04x3,55 = 0,538.
Variâncias:
V(X) = E(X2) – E2(X) = 1,74 – (1,04)2 = 0,6584.
V(Y) = E(Y2) – E2(Y) = 14,1 – (3,55)2 = 1,5275.
Cov xy 0,538
rxy = = = 0,536 = 53,6%.
σ xσ y 0,6584 ×1,5275
Covxy = 0,536 > 0 ⇒ X e Y aumentam no mesmo sentido;
Covxy = 0,536 > 0,5 ⇒ Э correlação forte entre X e Y.
Por: E. Seno 26
FE-UAN - 2006

27. Parâmetros de vectores aleatórios
Exemplos – resolução (v. a. Discretas):
Valor esperado condicional de X:
2 2
f ( x;2 )
E ( X Y = 2) = ∑
x=0
xf ( x Y = 2 ) = ∑ x
x=0 f y (2)
=
0,2 0 ,05 0 ,04
= 0× + 1× + 2× = 0 , 44828 .
0 , 29 0 , 29 0 , 29
X f(xi;2) f(xiY=2) xi.f(xiY=2)
0 0,2 0,6897 0
1 0,05 0,1724 0,17241
2 0,04 0,1379 0,27586
Σ 0,29 1 0,44828
Por: E. Seno 27
FE-UAN - 2006

28. Parâmetros de vectores aleatórios
Exemplos – resolução (v. a. Discretas):
Valor esperado condicional de Y:
5 5
f (1; y )
E ( Y X = 1) = ∑
y=2
yf ( y X = 1) = ∑ y
y=2 f x (1)
=
0 , 05 0 ,1 0 , 04 0 ,15
= 2× + 3× + 4× + 5× = 3 ,85 .
0 ,34 0 ,34 0 ,34 0 ,34
y 2 3 4 5 Σ
f(1;yj) 0,05 0,1 0,04 0,15 0,34
f(yjX=1) 0,15 0,29 0,12 0,44 1
yj.f(yjX=1) 0,29 0,88 0,47 2,21 3,85
Por: E. Seno 28
FE-UAN - 2006

29. Parâmetros de vectores aleatórios
Exemplos – resolução (v. a. contínuas):
Comecemos por determinar o valor esperado conjunto
1 1
+ +
+ ∞+ ∞ 2 2
1
E ( XY ) = ∫ ∫ xyf ( x , y ) dxdy = ∫ ∫ xydxdy =
− ∞− ∞
2 1 1
− −
2 2
+
1
⎡ + 12 ⎤ +
1
+
1
1 2
⎢ ⎥ 1 2
⎡ x2 ⎤ 2
=
2 ∫ y ⎢ ∫ xdx ⎥.dy =
2 ∫1
y⎢ ⎥
⎣ 2 ⎦−
.dy = 0
⎢− 1 ⎥
1 1
− −
2 ⎣ 2 ⎦ 2 2
Por: E. Seno 29
FE-UAN - 2006

30. Parâmetros de vectores aleatórios
Exemplos – resolução (v. a. contínuas):
Cálculo dos valores esperados marginais de X e de Y:
1
+
+∞ 2
1
E ( X ) = ∫ xf x ( x ) dx = ∫ xdx = 0.
−∞ 2 1
−
2
e
1
+
+∞ 2
1
E (Y ) = ∫ yf y ( y ) dy = ∫ ydy =0.
−∞ 2 1
−
2
Por: E. Seno 30
FE-UAN - 2006

31. Parâmetros de vectores aleatórios
Exemplos – resolução (v. a. contínuas):
Cálculo de E(X2) e E(Y2)
1
+
+∞ 2
1
E(X ) = ∫ x 2 f x ( x ) dx = ∫ x 2 dx =
2
−∞ 2 1
−
2
1
+
1 ⎡x ⎤ 3 2 1 ⎛ 1 1 ⎞ 1
⎢ ⎥ = ×⎜ + ⎟=
2 ⎣ 3 ⎦− 1 2×3 ⎝2 2 2 2 ⎠ 6
2
1
E (Y 2 ) = E ( X 2 ) =
6
V(X) = V(Y) = E(X2) – E2(X) =
Por: E. Seno 31
FE-UAN - 2006