O documento discute o conceito fundamental da integral definida no cálculo integral e sua aplicação no cálculo da área sob uma curva. A integral definida é calculada como o limite da soma de Riemann, que aproxima a área dividindo o intervalo em partes retangulares cada vez menores. Geometricamente, a integral representa exatamente a área sob a curva da função no intervalo dado.

1. CÁLCULO DIFERENCIAL E INTEGRAL II
Aula: 02
Temática: Soma de Riemann e a Integral Definida
Estudaremos agora um dos conceitos fundamentais do Cálculo
Integral: o cálculo da área sob a curva de uma função. Este conceito é de
grande importância no estudo de várias ciências como: matemática
(geometria), física, química, entre outras.
Integral de Riemann - Determinação da área sob uma curva
Ao calcularmos a área sob a curva da função x)x(f = entre os limites a e b,
conforme a figura a seguir, certamente calcularíamos a área do triângulo de
base igual a ( ab − ) e altura igual a ( )a(f)b(f − ), mais a área do retângulo de
base ( ab − ) e altura f(a), certo?
E se tentarmos calcular a área sob a curva da função no intervalo entre a e b,
conforme a figura a seguir?

2. CÁLCULO DIFERENCIAL E INTEGRAL II
Uma das formas seria dividir a região de interesse em intervalos retangulares
iguais (conforme a figura a seguir) e calcular a área aproximada como sendo a
soma destes intervalos. Vamos fazer uma tentativa dividindo a área sob a
curva em três pedaços:
A área sob a função x
e)x(f = seria aproximada por:
x)x(fx)x(fx)x(fA 332211 ∆∆∆ ++≅
onde xi∆ é igual a i1i xx −+ e )x(f i é valor médio de f(x) em xi∆ .
Entretanto, podemos perceber visualmente que esta aproximação não
representa exatamente a área sob a curva. Intuitivamente, se aumentarmos o
número de subdivisões do intervalo entre a e b, teremos retângulos com áreas
cada vez menores que se ajustaram melhor à função:

3. CÁLCULO DIFERENCIAL E INTEGRAL II
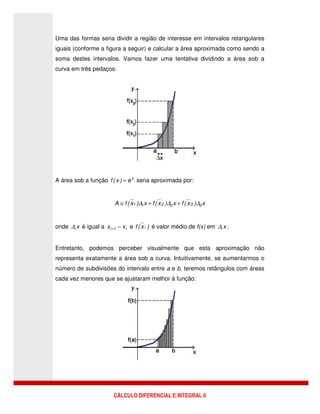
Dividindo o intervalo em n intervalos iguais, poderíamos aproximar a área
através do somatório:
∑
=
=++++=
n
1i
iinn332211 x)x(fx)x(f...x)x(fx)x(fx)x(fA ∆∆∆∆∆
Esta equação é chamada soma de Riemann.
E, dividindo o intervalo entre a e b em infinitas divisões iguais aproximando o
valor de ∆x á zero:
Calculamos o que é chamada de integral definida da função f em [a,b]:
∑∫ =
→
=
n
1i
ii
0x
b
a
x)x(flimdx)x(f ∆
∆
Esta expressão é numericamente igual à área sob a curva da função.
Geometricamente esta área seria difícil de calcular, mas, utilizando o Cálculo,
se torna muito mais fácil!
Outras propriedades da integral definida
a) 0dx)x(f
a
a
=∫
b) dx)x(fdx)x(f
a
b
b
a
∫∫ −=
c) dx)x(fdx)x(fdx)x(f
b
c
c
a
b
a
∫∫∫ +=

4. CÁLCULO DIFERENCIAL E INTEGRAL II
Nesta aula você aprendeu o conceito da integral definida e uma de
suas aplicações diretas: o cálculo da área sob uma curva. Na próxima aula
estudaremos outras aplicações da integral definida e faremos alguns
exercícios. Bons estudos!