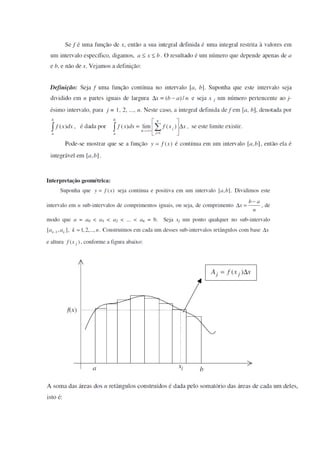
O documento discute integrais definidas e como elas podem ser usadas para calcular a variação de uma grandeza entre limites específicos. Ele fornece a definição matemática de integral definida e apresenta um exemplo numérico para ilustrar como calcular a quantidade pela qual uma população crescerá em um período de tempo usando uma integral definida. O documento também lista uma série de exercícios para serem resolvidos usando integrais definidas.

1. UNIVERSIDAD FERMIN TORO
CABUDARE ESTADO LARA
MATEMATICA II
JOSE CHAVEZ
C.I. 20942665
Integral Definida
Suponha que você conheça a taxa f(x) = dF/dx, na qual uma certa grandeza F
está variando e deseje encontrar a quantidade pela qual a grandeza F variará entre x = a
e x = b. Você pode primeiro encontrar F por antidiferenciação, e então calcular a
diferença:
Variação em F entre
x= a e x = b = F(b) – F(a)
O resultado numérico deste cálculo é chamado de integral definida da função f e
é denotado pelo símbolo:
∫
b
a
dxxf )(
O símbolo ∫
b
a
dxxf )( é lido como “ a integral definida de f de a até b”. Os
números a e b são denominados limites de integração. Nos cálculos que envolvem as
integrais definidas, é freqüentemente conveniente usar o símbolo:
b
axF )( para a diferença F(b) – F(a).
Ex.: Um estudo indica que, daqui a x meses a população de uma cidade estará crescendo
a uma taxa de 2 + x6 pessoas por mês. Em quanto a população crescerá durante os
próximos 4 meses?
Solução:
P(x) = população daqui a x meses, então a taxa da variação da população em relação ao
tempo dP/dx = 2 + x6 e a quantidade pela qual a população crescerá durante os
próximos 4 meses será a integral definida:
P(4) – P(0) = dx)x62(
4
0
∫ +
= 2 dx∫
4
0
+ 6 dx∫
4
0
1/2
x(
= 2x + 4
0
2/3
2/3
6
C
x
+
= 2x + 4x 2/3
+ C
4
0
= (2(4) + 4(4)3/2
+ C) – ( 2.(0) + 4(0) + C)
= 40 pessoas

6. Exercícios:
1. Calcular as integrais.
a) ∫−
+
2
1
3
)1( dxxx b) ∫−
+−
0
3
2
)74( dxxx
c) ∫
2
1
6
x
dx
d) ∫ +
1
0 13y
dy
e) ∫
4
3
4
cos
π
π
dxsenx f) ∫− +
1
1
3
2
9x
dxx
g) dxxx )1(
3
0
∫ +
2. Encontre a área da região limitada pelas curvas y = x2
+1 e y = 2x – 2 entre
x = -1 e x = 2.
3. Encontre a área da região limitada pelas curvas y = x3
e y = x2
.
4. Encontre a área da região limitada pela curva y = -x2
+ 4x – 3 e pelo eixo x.
5. Encontre a área da Região R no primeiro quadrante que se situa sob a curva
y = 1/x e é limitado por esta curva e pelas retas y = x, x=0 e x =2.
6. Encontre a área da região S, limitada pela curva y = senx e pelo eixo dos x de 0
até 2π.
7. Encontre a área limitada por y = x2
e y = x+2.
8. Encontre a área limitada pelas curvas y = x2
– 1 e y = x +1. As curvas
interceptam-se nos pontos de abscissa -1 e 2.

7. Exercícios:
1. Calcular as integrais.
a) ∫−
+
2
1
3
)1( dxxx b) ∫−
+−
0
3
2
)74( dxxx
c) ∫
2
1
6
x
dx
d) ∫ +
1
0 13y
dy
e) ∫
4
3
4
cos
π
π
dxsenx f) ∫− +
1
1
3
2
9x
dxx
g) dxxx )1(
3
0
∫ +
2. Encontre a área da região limitada pelas curvas y = x2
+1 e y = 2x – 2 entre
x = -1 e x = 2.
3. Encontre a área da região limitada pelas curvas y = x3
e y = x2
.
4. Encontre a área da região limitada pela curva y = -x2
+ 4x – 3 e pelo eixo x.
5. Encontre a área da Região R no primeiro quadrante que se situa sob a curva
y = 1/x e é limitado por esta curva e pelas retas y = x, x=0 e x =2.
6. Encontre a área da região S, limitada pela curva y = senx e pelo eixo dos x de 0
até 2π.
7. Encontre a área limitada por y = x2
e y = x+2.
8. Encontre a área limitada pelas curvas y = x2
– 1 e y = x +1. As curvas
interceptam-se nos pontos de abscissa -1 e 2.