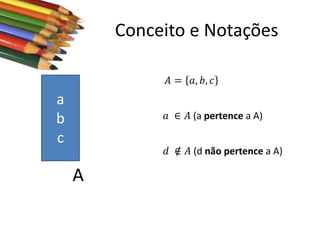
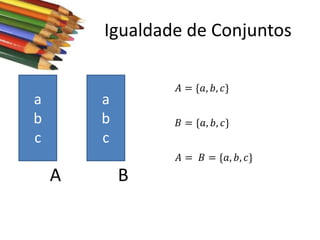
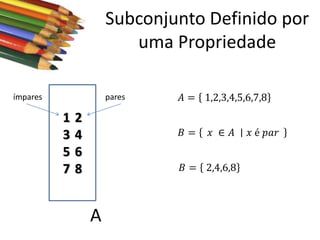
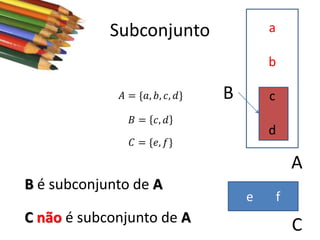
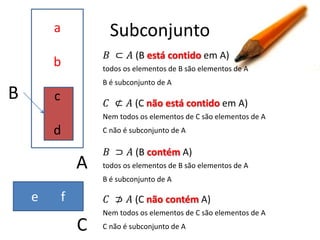
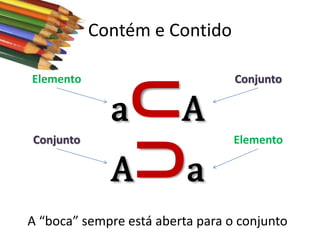
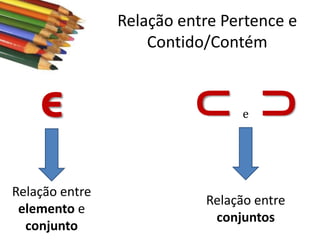
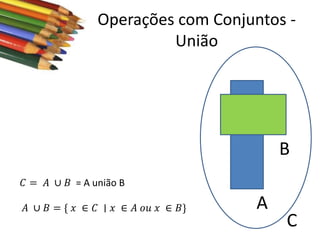
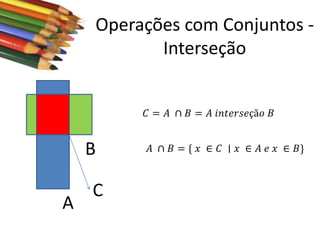
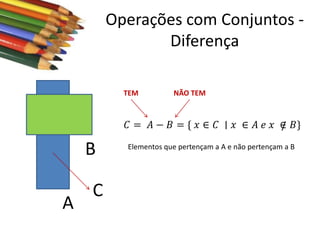
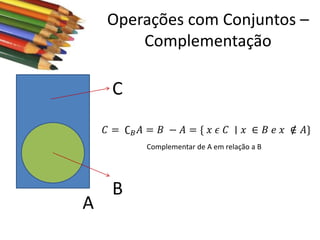
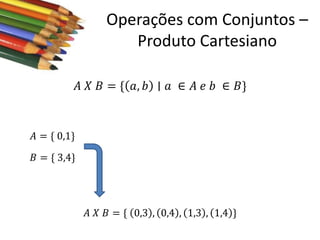
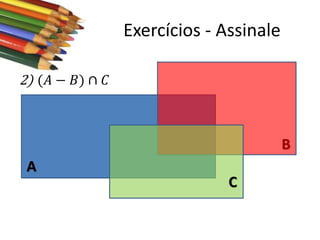
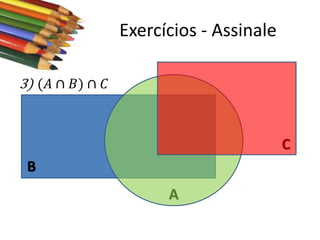
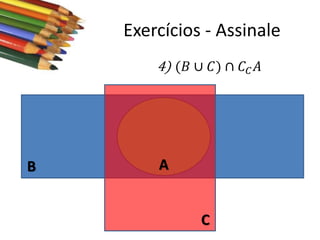
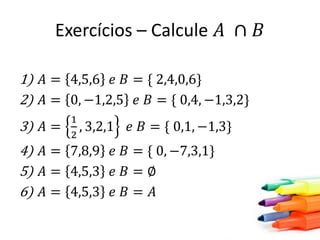Este documento apresenta conceitos básicos sobre conjuntos, incluindo notações, igualdade, subconjuntos, operações (união, interseção, diferença, complementação, produto cartesiano) e conjuntos numéricos importantes. O documento é uma aula sobre conjuntos ministrada pelo professor Milton Henrique.

1. Unidade 1 - Conjuntos
Prof. Milton Henrique
mcouto@catolica-es.edu.br

2. Conceito e Notações
𝐴 = 𝑎, 𝑏, 𝑐
a
b
c
𝑎 ∈ 𝐴 (a pertence a A)
/
𝑑 ∈ 𝐴 (d não pertence a A)
A

3. Igualdade de Conjuntos
a
b
c
𝐴 = {𝑎, 𝑏, 𝑐}
a
b
c
𝐵 = {𝑎, 𝑏, 𝑐}
𝐴 = 𝐵 = {𝑎, 𝑏, 𝑐}
A
B

4. Subconjunto Definido por
uma Propriedade
ímpares
pares
1
3
5
7
2
4
6
8
𝐴 = 1,2,3,4,5,6,7,8
𝐵=
𝑥 ∈ 𝐴
𝐵 = 2,4,6,8
A
𝑥 é 𝑝𝑎𝑟

5. Exercícios
1 3
10
−2, 1, 0, , , 2, , 4, −5
2 4
3
Seja 𝐴 =
, explicite os
elementos de cada um dos subconjuntos abaixo:
1) {𝑥 ∈ 𝐴 ∣ 𝑥 < 0}
2) {𝑥 ∈ 𝐴 ∣ 2 < 𝑥 < 3}
3) {𝑥 ∈ 𝐴 ∣ 𝑥 ≤ 0}
4) {𝑥 ∈ 𝐴 ∣ 𝑥 2 = 4}
5) {𝑥 ∈ 𝐴 ∣ 2 − 3. 𝑥 ≤ 0}

6. a
Subconjunto
b
𝐴 = {𝑎, 𝑏, 𝑐, 𝑑}
B
c
𝐵 = 𝑐, 𝑑
d
𝐶 = {𝑒, 𝑓}
A
B é subconjunto de A
C não é subconjunto de A
e
f
C

7. a
Subconjunto
𝐵 ⊂ 𝐴 (B está contido em A)
b
todos os elementos de B são elementos de A
B é subconjunto de A
B
c
𝐶 ⊄ 𝐴 (C não está contido em A)
Nem todos os elementos de C são elementos de A
d
C não é subconjunto de A
A
𝐵 ⊃ 𝐴 (B contém A)
todos os elementos de B são elementos de A
B é subconjunto de A
e
f
𝐶 ⊅ 𝐴 (C não contém A)
C
Nem todos os elementos de C são elementos de A
C não é subconjunto de A

8. Subconjunto
⊂e⊄
 Contido
 Não contido
⊃e⊅
 Contém
 Não contém

9. Contém e Contido
⊂A
A⊃a
a
O elemento a ESTÁ
CONTIDO no conjunto A
O conjunto A CONTÉM o
elemento a

10. Contém e Contido
Elemento
⊂A
A⊃a
Conjunto
a
Conjunto
Elemento
A “boca” sempre está aberta para o conjunto

11. Pertence e Não Pertence
a
b
c
e
f
g
A
a ϵ A → a pertence a A
f ϵ A → f não pertence a A
B

12. Relação entre Pertence e
Contido/Contém
ϵ
⊂ ⊃
Relação entre
elemento e
conjunto
Relação entre
conjuntos
e

13. Operações com Conjuntos União
B
𝐶 = 𝐴 ∪ 𝐵 = A união B
𝐴 ∪ 𝐵 = { 𝑥 ∈ 𝐶 ∣ 𝑥 ∈ 𝐴 𝑜𝑢 𝑥 ∈ 𝐵}
A
C

14. Propriedades da União
𝐴 ∪ 𝐵= 𝐵 ∪ 𝐴
𝑐𝑜𝑚𝑢𝑡𝑎𝑡𝑖𝑣𝑎
𝐴∪ 𝐵 ∪ 𝐶 = 𝐴∪ 𝐵∪ 𝐶
𝐴 ∪ 𝐴= 𝐴
𝐴 ∪ ∅= 𝐴
𝐴 ∪ 𝐸 = 𝐸, 𝑠𝑒 𝐴 ⊂ 𝐸
𝑎𝑠𝑠𝑜𝑐𝑖𝑎𝑡𝑖𝑣𝑎

15. Exercícios - Calcule 𝐴 ∪ 𝐵
1) 𝐴 = 4,5,3 𝑒 𝐵 = { 0,3,1}
2) 𝐴 = 2,0, −1 𝑒 𝐵 = { −1,0,5}
3) 𝐴 =
1
4,5, , 0
2
𝑒 𝐵 = { −1,4,0,2}
4) 𝐴 = 4,2,9 𝑒 𝐵 = ∅
5) 𝐴 = 4,5,3 𝑒 𝐵 = 𝐴

16. Operações com Conjuntos Interseção
𝐶 = 𝐴 ∩ 𝐵 = 𝐴 𝑖𝑛𝑡𝑒𝑟𝑠𝑒çã𝑜 𝐵
B
A
C
𝐴 ∩ 𝐵 = { 𝑥 ∈ 𝐶 ∣ 𝑥 ∈ 𝐴 𝑒 𝑥 ∈ 𝐵}

17. Propriedades da Interseção
𝐴 ∩ 𝐵= 𝐵 ∩ 𝐴
𝑐𝑜𝑚𝑢𝑡𝑎𝑡𝑖𝑣𝑎
𝐴∩ 𝐵 ∩ 𝐶 = 𝐴∩ 𝐵∩ 𝐶
𝑎𝑠𝑠𝑜𝑐𝑖𝑎𝑡𝑖𝑣𝑎
𝐴 ∩ 𝐴= 𝐴
𝐴 ∩ ∅=∅
𝐴 ∩ 𝐸 = 𝐴, 𝑠𝑒 𝐴 ⊂ 𝐸
𝐴∪ 𝐵∩ 𝐶 =
𝐴∪ 𝐵 ∩ 𝐴∪ 𝐶
𝑑𝑖𝑠𝑡𝑟𝑖𝑏𝑢𝑡𝑖𝑣𝑎
𝐴∩ 𝐵∪ 𝐶 =
𝐴∩ 𝐵 ∪ 𝐴∩ 𝐶
𝑑𝑖𝑠𝑡𝑟𝑖𝑏𝑢𝑡𝑖𝑣𝑎

18. Exercícios – Calcule 𝐴 ∩ 𝐵
1) 𝐴 = 4,5,6 𝑒 𝐵 = { 2,4,0,6}
2) 𝐴 = 0, −1,2,5 𝑒 𝐵 = { 0,4, −1,3,2}
3) 𝐴 =
1
, 3,2,1
2
𝑒 𝐵 = { 0,1, −1,3}
4) 𝐴 = 7,8,9 𝑒 𝐵 = { 0, −7,3,1}
5) 𝐴 = 4,5,3 𝑒 𝐵 = ∅
6) 𝐴 = 4,5,3 𝑒 𝐵 = 𝐴

19. Operações com Conjuntos Diferença
TEM
NÃO TEM
𝐶 = 𝐴 − 𝐵 = { 𝑥 ∈ 𝐶 ∣ 𝑥 ∈ 𝐴 𝑒 𝑥 ∈ 𝐵}
/
B
A
C
Elementos que pertençam a A e não pertençam a B

20. Exercícios – Calcule 𝐴 − 𝐵
TEM
1) 𝐴 = 4,5,3,1 𝑒 𝐵 = { 4,2,1}
2) 𝐴 =
1
0,1, −1,
2
𝑒 𝐵={
1
4,2,0, }
2
3) 𝐴 = 3,4,5 𝑒 𝐵 = { 2,1,6}
4) 𝐴 = 4,5,3 𝑒 𝐵 = ∅
5) 𝐴 = 4,5,3 𝑒 𝐵 = 𝐴
NÃO TEM

21. Operações com Conjuntos –
Complementação
C
/
𝐶 = ∁ 𝐵 𝐴 = 𝐵 − 𝐴 = { 𝑥 𝜖 𝐶 ∣ 𝑥 ∈ 𝐵 𝑒 𝑥 ∈ 𝐴}
Complementar de A em relação a B
A
B

22. Exercícios – Calcule ∁ 𝐵 𝐴
1)
2)
3)
4)
5)
6)
𝐴=
𝐴=
𝐴=
𝐴=
𝐴=
𝐴=
4,5,6 𝑒
1,2,3 𝑒
−1,5,2
0,8,10
4,5,3 𝑒
4,5,3 𝑒
𝐵 = { 0,1, 2,4,5,6,7}
𝐵 = 0,1,4,3,6,2
𝑒 𝐵 = { 2, −1,5}
𝑒 𝐵 = 1,0,8,10
𝐵= ∅
𝐵= 𝐴

23. Operações com Conjuntos –
Produto Cartesiano
𝐴 𝑋 𝐵 = { 𝑎, 𝑏 ∣ 𝑎 ∈ 𝐴 𝑒 𝑏 ∈ 𝐵}
𝐴 = { 0,1}
𝐵 = { 3,4}
𝐴 𝑋 𝐵 = { 0,3 , 0,4 , 1,3 , 1,4 }

24. Exercícios – Calcule 𝐴 𝑋 𝐵
1)
2)
3)
4)
5)
𝐴=
𝐴=
𝐴=
𝐴=
𝐴=
4,5,3 𝑒
0,2,1,5
𝑎, 𝑏, 𝑐, 𝑑
1,2,3 𝑒
4,5,6 𝑒
𝐵 = { 0,3,1}
𝑒 𝐵 = 5,1,6,4
𝑒 𝐵 = { 𝑎, 𝑏, 𝑑}
𝐵 = { 4,5}
𝐵 = { 0}

25. Exercícios - Assinale
1) 𝐴 ∩ (𝐵 − 𝐴)
A
B

26. Exercícios - Assinale
2) (𝐴 − 𝐵) ∩ 𝐶
B
A
C

27. Exercícios - Assinale
3) (𝐴 ∩ 𝐵) ∩ 𝐶
C
B
A

28. Exercícios - Assinale
4) (𝐵 ∪ 𝐶) ∩ 𝐶 𝐶 𝐴
B
A
C

29. Exercícios - Assinale
5) (𝐴 ∪ 𝐵) ∩ (𝐵 ∩ 𝐶)
A
C
B

30. Conjuntos Numéricos Importantes
𝑁 = 0,1,2,3,4, …
𝑁ú𝑚𝑒𝑟𝑜𝑠 𝑁𝑎𝑡𝑢𝑟𝑎𝑖𝑠
𝑍 = 0, ±1, ±2, ±3, ±4, …
𝑄=
𝑎
∣ 𝑎 ∈ 𝑍, 𝑏 ∈ 𝑍, 𝑏 ≠ 0
𝑏
𝑁ú𝑚𝑒𝑟𝑜𝑠 𝐼𝑛𝑡𝑒𝑖𝑟𝑜𝑠
𝑁ú𝑚𝑒𝑟𝑜𝑠 𝑅𝑎𝑐𝑖𝑜𝑛𝑎𝑖𝑠
Parte decimal finita ou dízimas periódicas
𝐼=
2, 𝜋, …
𝑁ú𝑚𝑒𝑟𝑜𝑠 𝐼𝑟𝑟𝑎𝑐𝑖𝑜𝑛𝑎𝑖𝑠
Parte decimal infinita não periódica
𝑅= 𝐼 ∪ 𝑄
𝑁ú𝑚𝑒𝑟𝑜𝑠 𝑅𝑒𝑎𝑖𝑠

31. Conjuntos Numéricos Importantes
Racionais
Inteiros
Naturais
Reais
Irracionais

32. Quem sou eu?
Prof. Milton Henrique do Couto Neto
mcouto@catolica-es.edu.br
Engenheiro Mecânico, UFF
MBA em Gestão Empresarial, UVV
MBA em Marketing Empresarial, UVV
Mestre em Administração, UFES
Pós-MBA em Inteligência Empresarial, FGV
http://lattes.cnpq.br/8394911895758599

33. Professor Universitário
2004
2011
2006
2007
2009
2011

34. Disciplinas
Lecionadas
Marketing
Empreendedorismo
Administração de Materiais
Matemática
Matemática Financeira
Gestão Financeira
Fundamentos da Administração
Gestão de Processos e Empresas

35. miltonhenrique
miltonhcouto
miltonhcouto

36. Este e outros arquivos estão
disponíveis para download no
www.slideshare.net/miltonh