1) O documento apresenta conceitos básicos de matemática, incluindo conjuntos, números, operações com conjuntos e frações.
2) É definido o que são conjuntos, subconjuntos, união, interseção e diferença de conjuntos. Também são explicados os conjuntos numéricos fundamentais.
3) O texto descreve intervalos numéricos, partição de conjuntos e a fórmula para calcular o número de elementos da união de dois conjuntos. Por fim, é apresentada a definição de fração.


![____________ _____________________________ MATEMÁTICA _________________________________ Prof. Roberto
__________________________________________________________________________________________________________________________
ATUALIZADO ATÉ MAIO/2012 www.CARREIRAPUBLICA.com.br (48) 4141-3220 4141-3222
2
2/3, -3/7, 0,001=1/1000, 0,75=3/4, 0,333... = 1/3, 7 = 7/1, etc.
Notas:
a) é evidente que N ⊂
⊂
⊂
⊂ Z ⊂
⊂
⊂
⊂ Q.
b) toda dízima periódica é um número racional, pois é sempre possível escrever uma dízima periódica na forma de
uma fração.
Exemplo: 0,4444... = 4/9
Conjunto dos números irracionais
I = {x; x é uma dízima não periódica}.
Exemplos de números irracionais:
π = 3,1415926... (número pi = razão entre o comprimento de qualquer circunferência e o seu diâmetro)
2,01001000100001... (dízima não periódica)
√ 3 = 1,732050807... (raiz não exata).
Conjunto dos números reais
R = { x; x é racional ou x é irracional}.
Notas:
a) é óbvio que N ⊂ Z ⊂ Q ⊂ R
b) I ⊂ R
c) I ∪ Q = R
d) um número real é racional ou irracional, não existe outra hipótese!
1.4 Intervalos numéricos
Dados dois números reais p e q, chama-se intervalo a todo conjunto de todos números reais compreendidos entre p
e q , podendo inclusive incluir p e q. Os números p e q são os limites do
intervalo, sendo a diferença p - q , chamada amplitude do intervalo.
Se o intervalo incluir p e q , o intervalo é fechado e caso contrário, o intervalo é dito aberto.
A tabela abaixo, define os diversos tipos de intervalos.
TIPOS REPRESENTAÇÃO OBSERVAÇÃO
INTERVALO FECHADO [p;q] = {x ∈
∈
∈
∈ R; p ≤
≤
≤
≤ x ≤
≤
≤
≤ q} inclui os limites p e q
INTERVALO ABERTO (p;q) = { x ∈
∈
∈
∈ R; p <
<
<
< x <
<
<
< q} exclui os limites p e q
INTERVALO FECHADO A ESQUERDA [p;q) = { x ∈
∈
∈
∈ R; p ≤
≤
≤
≤ x <
<
<
< q} inclui p e exclui q
INTERVALO FECHADO À DIREITA (p;q] = {x ∈
∈
∈
∈ R; p <
<
<
< x ≤
≤
≤
≤ q} exclui p e inclui q
INTERVALO SEMI-FECHADO [p;∞
∞
∞
∞ ) = {x ∈
∈
∈
∈ R; x ≥
≥
≥
≥ p} valores maiores ou iguais a p.
INTERVALO SEMI-FECHADO (- ∞
∞
∞
∞ ; q] = { x ∈
∈
∈
∈ R; x ≤
≤
≤
≤ q} valores menores ou iguais a q.
INTERVALO SEMI-ABERTO (-∞
∞
∞
∞ ; q) = { x ∈
∈
∈
∈ R; x <
<
<
< q} valores menores do que q.
INTERVALO SEMI-ABERTO (p; ∞
∞
∞
∞ ) = { x >
>
>
> p } valores maiores do que p.
Nota: é fácil observar que o conjunto dos números reais, (o conjunto R) pode ser representado na forma de intervalo
como R = ( -∞
∞
∞
∞ ; + ∞
∞
∞
∞ ).
1.5 Operações com conjuntos
1.5.1 União ( ∪
∪
∪
∪ )
Dados os conjuntos A e B , define-se o conjunto união A ∪
∪
∪
∪ B = { x; x ∈
∈
∈
∈ A ou x ∈
∈
∈
∈ B}.
Exemplo: {0,1,3} ∪ { 3,4,5 } = { 0,1,3,4,5}.
Percebe-se facilmente que o conjunto união contempla todos os elementos do conjunto A ou do conjunto B.
Propriedades imediatas:
a) A ∪ A = A
b) A ∪ φ = A](https://image.slidesharecdn.com/7463apostilamatematicaprofroberto-230301234649-780450f5/85/7463_APOSTILA_Matematica_Prof_Roberto-pdf-3-320.jpg)













![____________ _____________________________ MATEMÁTICA _________________________________ Prof. Roberto
__________________________________________________________________________________________________________________________
ATUALIZADO ATÉ MAIO/2012 www.CARREIRAPUBLICA.com.br (48) 4141-3220 4141-3222
16
b) potência de expoente unitário : a1
= a
Exemplos: 23
1
= 23; 2001
1
= 2001.
As potências de expoente 2 e 3 recebem nomes especiais, a saber:
a
2
= a.a, é lido como a ao quadrado.
a
3
= a.a.a, é lido como a ao cubo.
5.2 Propriedades das potências
São válidas as seguintes propriedades das potências de expoentes naturais, facilmente demonstráveis:
P1) a
m
. a
n
= a
m+n
Exemplo: 2
5
.2
3
= 2
5+3
= 2
8
= 2.2.2.2.2.2.2.2 = 256
P2) a
m
: a
n
= a
m-n
Exemplo: 5
7
:5
4
= 5
7-4
= 5
3
= 5.5.5 = 125
P3) (a
m
)
n
= a
m.n
Exemplo: (4
2
)
3
= 4
2.3
= 4
6
= 4.4.4.4.4.4 = 4096
P4) a
m
.b
m
= (a.b)
m
Exemplo: 2
3
.4
3
= (2.4)
3
= 8
3
= 8.8.8 = 512
P5) a
m
:b
m
= (a:b)
m
Exemplo: 12
4
:3
4
= (12:3)
4
= 4
4
= 4.4.4.4 = 256
P6) a
-n
= 1/a
n
Exemplo: 5
-2
= 1/5
2
= 1/5.5 = 1/25
Esta propriedade decorre de P2, ou seja: a
-n
= a
0
/a
n
= a
0-n
= a
-n
.
Nota: estas propriedades também são válidas para expoentes reais.
Exercício:
Calcule o valor da expressão a seguir:
A = {[(2
3
.2
4
: 4
3
)]
5
}
-2
Desenvolvimento:
A = {[(2
7
: (2
2
)
3
)]
5
}
-2
= {[2
7
: 2
6
]
5
}
-2
= {[2
1
]
5
}
-2
= 2
-10
= 1/2
10
= 1/1024
6 Radicais
A forma mais genérica de um radical é:
onde c = coeficiente, n = índice e A = radicando.
O radical acima é lido como: c raiz n-ésima (enésima) de A.
Se n = 2, costuma-se não representar o número 2 e lê-se como c raiz quadrada de A.](https://image.slidesharecdn.com/7463apostilamatematicaprofroberto-230301234649-780450f5/85/7463_APOSTILA_Matematica_Prof_Roberto-pdf-17-320.jpg)











![____________ _____________________________ MATEMÁTICA _________________________________ Prof. Roberto
__________________________________________________________________________________________________________________________
ATUALIZADO ATÉ MAIO/2012 www.CARREIRAPUBLICA.com.br (48) 4141-3220 4141-3222
28
58. ( CORREIOS – 2006 ) O valor da expressão [(-2)³-(-3)³]+[(-2)
4
+(-2)³] é igual a
a) -8. b) 8. c) 16. d) -27. e) 27.
59. Calcule: a) 5
2
b) ( -5 )
2
c) ( -2 )
3
d) 3
0
e) 243
1
f) 1
7
g)
2
3
2
−
h) ( ) 1
5
,
0
−
i) ( )3
2
2
60. O valor da expressão 6
6
+ 6
6
+ 6
6
+ 6
6
+ 6
6
+ 6
6
é:
a) 6
6
b) 6
7
c) 7
6
d) 6
36
e) 36
6
61. Qual a metade de 2
22
?
a) 2
11
b) 1
22
c) 1
11
d) 2
21
e) n.d.a
62. Calcule
5
,
0
3
2
9
8 +
63. Uma calculadora apresentava, em sua tela, o resultado da soma dos gastos do mês realizados por um pai
"coruja" que permitiu a seu filho apertar algumas teclas, alterando esse resultado. O pai observou que o menino
havia apertado as teclas, uma única vez, na ordem mostrada na figura 1.
Para recuperar o resultado que estava na tela, o pai deverá apertar as teclas.
64. Calcule as seguintes raízes:
a) 81 b) 400 c) 3
216
d) 4
256
65. Simplifique as seguintes raízes:
a) 12 b) 192
c) 3
108 d) 4
48
66. A expressão 12
3
27
48
2
75
3 +
−
− vale:
a) 3
10 b) 3
12 c) 3
6
d) 3
4 e) 15
67. Simplifique a expressão: 6
24
2
150
54 +
+
−
68. Efetue: 1445
125
20
2
1
5
4 −
+
−
69. Racionalize os denominadores.
a)
2
3
b)
2
2
8
c)
5
2
5](https://image.slidesharecdn.com/7463apostilamatematicaprofroberto-230301234649-780450f5/85/7463_APOSTILA_Matematica_Prof_Roberto-pdf-29-320.jpg)




















































![____________ _____________________________ MATEMÁTICA _________________________________ Prof. Roberto
__________________________________________________________________________________________________________________________
ATUALIZADO ATÉ MAIO/2012 www.CARREIRAPUBLICA.com.br (48) 4141-3220 4141-3222
86
0
2
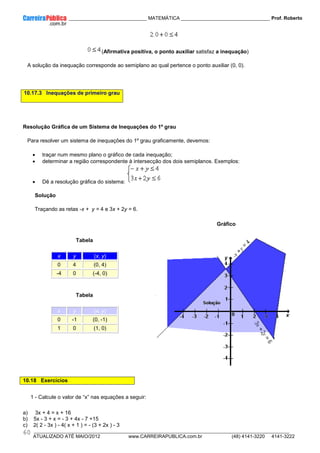
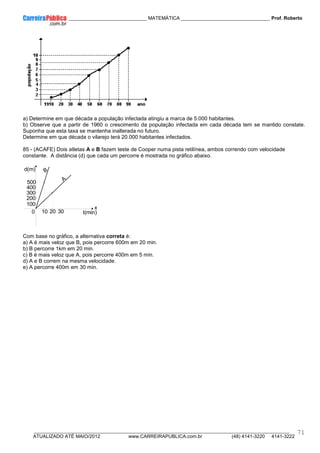
b) Se a<0 Ex.: y = –x²–1
11.11.2 COORDENADAS DO VÉRTICE DA PARÁBOLA
O vértice é formado pela abscissa xv e a ordenada yv:
∆
−
−
a
4
,
a
2
b
V
Obs.: Para a>0, o ponto V do vértice é ponto de mínimo da função.
Para a<0 o ponto V do vértice é ponto de máximo da função.
11.11.3 Imagem da função quadrática
A imagem dessa função é obtida projetando-se ortogonalmente os pontos da parábola no eixo y. Desse modo a
ordenada yv será sempre um dos extremos do intervalo do conjunto imagem, observe:
a>0
Im = [yv, +∞ )
a<0
Im =(+∞ , yv]
11.12 Exercícios
1 - Calcule as raízes das equações abaixo:
a) x² - 7x + 10 = 0 b) 2x² - 20x + 18 = 0 c) - x² + 10x - 21 = 0 d) (x + 3)(x - 5) = 0 e) (x - 1)(x - 2) = 0
f) (x + 5)² = 0
2 - Calcule a soma das raízes da equação 2x² - 6x - 5 = 0 ( Ag. Adm. - SC)
3 - Qual o valor de p para que a equação 3x² - 6x + p = 0 tenha raízes reais e iguais? ( ESA)
4 - Calcule a soma e o produto das raízes da equação 5x² + 3x - 4 = 0 (ESA)
5 - Qual a equação, cujas raízes são 7 e - 2 ? ( Exator - SC)
x
y
-2 -1 0 1 2
-4
-2
0
y
x
xv
V
yv
0
2
yv
V
xv
x
y
X1 X2
f(X2)
f(X1)](https://image.slidesharecdn.com/7463apostilamatematicaprofroberto-230301234649-780450f5/85/7463_APOSTILA_Matematica_Prof_Roberto-pdf-87-320.jpg)





























![____________ _____________________________ MATEMÁTICA _________________________________ Prof. Roberto
__________________________________________________________________________________________________________________________
ATUALIZADO ATÉ MAIO/2012 www.CARREIRAPUBLICA.com.br (48) 4141-3220 4141-3222
117
tipo:
(x - r, x, x + r), onde r é a razão da PA.
Numa PA, a soma dos termos eqüidistantes dos extremos é constante.
Exemplo:
PA : ( m, n, r, s, t); portanto, m + t = n + s = r + r = 2r
Estas propriedades facilitam sobremaneira a solução de problemas.
5 - Soma dos n primeiros termos de uma PA
Seja a PA ( a1, a2, a3, ..., an-1, an).
A soma dos n primeiros termos Sn = a1 + a2 + a3 + ... + an-1 + an , pode ser deduzida facilmente, da aplicação
da segunda propriedade acima.
Temos:
Sn = a1 + a2 + a3 + ... + an-1 + an
É claro que também poderemos escrever a igualdade acima como:
Sn = an + an-1 + ... + a3 + a2 + a1
Somando membro a membro estas duas igualdades, vem:
2. Sn = (a1 + an) + (a2 + an-1) + ... + (an + a1)
Logo, pela segunda propriedade acima, as n parcelas entre parênteses possuem o mesmo valor ( são iguais
à soma dos termos extremos a1 + an ) , de onde concluímos inevitavelmente que:
2.Sn = (a1 + an).n , onde n é o número de termos da PA.
Daí então, vem finalmente que:
Exemplo:
Calcule a soma dos 200 primeiros números ímpares positivos.
Temos a PA: ( 1, 3, 5, 7, 9, ... )
Precisamos conhecer o valor de a200 .
Mas, a200 = a1 + (200 - 1).r = 1 + 199.2 = 399
Logo, Sn = [(1 + 399). 200] / 2 = 40.000
Portanto, a soma dos duzentos primeiros números ímpares positivos é igual a 40000.
15.5 Exercícios resolvidos
1 - Qual é o número mínimo de termos que se deve somar na P.A. :( 7/5 , 1 , 3/5 , ... ) , a partir do primeiro
termo, para que a soma seja negativa?
a) 9 *
b) 8
c) 7
d ) 6
e) 5
SOLUÇÃO:
Temos: a1 = 7/5 e r = 1 – 7/5 = 5/5 – 7/5 = -2/5, ou seja: r = -2/5.
Poderemos escrever então, para o n-ésimo termo an:
an = a1 + (n – 1).r = 7/5 + (n – 1).(-2/5)
an = 7/5 – 2n/5 + 2/5 = (7/5 + 2/5) –2n/5 = 9/5 –2n/5 = (9 – 2n)/5](https://image.slidesharecdn.com/7463apostilamatematicaprofroberto-230301234649-780450f5/85/7463_APOSTILA_Matematica_Prof_Roberto-pdf-118-320.jpg)
![____________ _____________________________ MATEMÁTICA _________________________________ Prof. Roberto
__________________________________________________________________________________________________________________________
ATUALIZADO ATÉ MAIO/2012 www.CARREIRAPUBLICA.com.br (48) 4141-3220 4141-3222
118
A soma dos n primeiros termos, pela fórmula vista anteriormente será então:
Sn = (a1 + an). (n/2) = [(7/5) + (9 – 2n)/5].(n/2) = [(16 – 2n)/5].(n/2)
Sn = (16n – 2n
2
) / 10
Ora, nós queremos que a soma Sn seja negativa; logo, vem:
(16n – 2n
2
) / 10 < 0
Como o denominador é positivo, para que a fração acima seja negativa, o numerador deve ser negativo.
Logo, deveremos ter:
16n – 2n
2
< 0
Portanto, n(16 – 2n ) < 0
Ora, como n é o número de termos, ele é um número inteiro e positivo. Portanto, para que o produto acima
seja negativo, deveremos ter:
16 – 2n < 0, de onde vem 16 < 2n ou 2n > 16 ou n > 8.
Como n é um número inteiro positivo, deduzimos imediatamente que n = 9.
Portanto, a alternativa correta é a letra A.
2 - As medidas dos lados de um triângulo são expressas por x + 1, 2x , x
2
- 5 e estão em P.A. , nesta ordem.
O perímetro do triângulo vale:
a) 8 b) 12 c) 15 *d) 24 e) 33
SOLUÇÃO:
Ora, se x + 1, 2x , x
2
– 5 formam uma P.A. , podemos escrever:
2x – (x + 1) = (x
2
– 5) – 2x
2x – x –1 + 5 – x
2
+ 2x = 0
3x + 4 – x
2
= 0
Multiplicando por (-1) ambos os membros da igualdade acima, fica:
x
2
– 3x – 4 = 0
Resolvendo a equação do segundo grau acima encontraremos x = 4 ou x = - 1.
Assim, teremos:
x = 4: os termos da P.A . serão: x+1, 2x, x
2
– 5 ou substituindo o valor de x encontrado: 5, 8, 11, que são as
medidas dos lados do triângulo. Portanto, o perímetro do triângulo (soma das medidas dos lados) será igual a
5+8+11 = 24.
O valor negativo de x não serve ao problema, já que levaria a valores negativos para os lados do triângulo, o
que é uma impossibilidade matemática, pois as medidas dos lados de um triângulo são necessariamente
positivas. Portanto, a alternativa correta é a letra D.
3 - UFBA - Um relógio que bate de hora em hora o número de vezes correspondente a cada hora, baterá , de
zero às 12 horas x vezes. Calcule o dobro da terça parte de x.
Resp: 60
SOLUÇÃO:
Teremos que:
0 hora o relógio baterá 12 vezes. (Você não acha que bateria 0 vezes, não é?).
1 hora o relógio baterá 1 vez
2 horas o relógio baterá 2 vezes
3 horas o relógio baterá 3 vezes
....................................................
....................................................
12 horas o relógio baterá 12 vezes.
Logo, teremos a seguinte seqüência:
(12, 1, 2, 3, 4, 5, ... , 12)
A partir do segundo termo da seqüência acima, temos uma PA de 12 termos, cujo primeiro termo é igual a 1,
a razão é 1 e o último termo é 12.](https://image.slidesharecdn.com/7463apostilamatematicaprofroberto-230301234649-780450f5/85/7463_APOSTILA_Matematica_Prof_Roberto-pdf-119-320.jpg)

![____________ _____________________________ MATEMÁTICA _________________________________ Prof. Roberto
__________________________________________________________________________________________________________________________
ATUALIZADO ATÉ MAIO/2012 www.CARREIRAPUBLICA.com.br (48) 4141-3220 4141-3222
120
a. 63
b. 65
c. 92
d. 95
e. 98
2. (FEI-SP) – A razão de uma PA de 10 termos, onde o primeiro termo é 42 e o último é –12, vale:
a. -5
b. -9
c. -6
d. -7
e. 0
3. O termo geral de uma PA é dado por an = 2n – 1. Então o terceiro termo da PA vale:
a. 2
b. 3
c. 5
d. 6
e. 4
4. (PUC – PR) – Calculando o número de termos de uma PA, onde o primeiro termo é 0,5 , o último termo é 45,5 e a
razão é 1,5, obtém-se:
a. 45
b. 38
c. 43
d. 31
e. 57
5. (FEI-SP) – O 10º termo da PA (a, 3a/2, ...) é igual a :
a. 11a/2
b. 9a/2
c. 7a/2
d. 13a/2
e. 15a/2
6. (UFPA) – Numa progressão aritmética, temos a7 = 5 e a15 = 61. Então, a razão pertence ao intervalo:
a. [8,10]
b. [6,8[
c. [4,6[
d. [2,4[
e. [0,2[
7. (MACK-SP) – O produto das raízes da equação x² + 2x – 3 = 0 é a razão de uma PA de primeiro termo 7. O 100º
termo dessa PA é:
a. -200
b. -304
c. -290
d. -205
e. -191
8. (UFRS) – O número de múltiplos de 7 entre 50 e 1206 é:
a. 53
b. 87
c. 100](https://image.slidesharecdn.com/7463apostilamatematicaprofroberto-230301234649-780450f5/85/7463_APOSTILA_Matematica_Prof_Roberto-pdf-121-320.jpg)










![____________ _____________________________ MATEMÁTICA _________________________________ Prof. Roberto
__________________________________________________________________________________________________________________________
ATUALIZADO ATÉ MAIO/2012 www.CARREIRAPUBLICA.com.br (48) 4141-3220 4141-3222
131
Logo, concluímos que N = 200/75
Simplificando, fica:
N = 40/15 = 8/3
Logo, 30N = 30(8/3) = 80 Resp: 30N = 80
16.6 EXERCÍCIOS PROPOSTOS
1 - UFBA - Sendo log2 = 0,301 e x = 5
3
. , então o logx é:
*a) 2,997 b) 3,398 c) 3,633 d) 4,398 e) 5,097
2 - UEFS - O produto das raízes da equação log(x
2
-7x + 14) = 2log2 é:
01) 5 02) 7 *03) 10 04) 14 05) 35
3 - UCSal - Se 12
n+1
= 3
n+1
. 8 , então log2 n é igual a:
a) -2 *b) -1 c) 1/2 d) 1 e) 2
4 - UEFS - O domínio da função y = log [(2x-3)/(4-x)] é:
a) (-3/2,4) b) (-4,3/2) c) (-4,2) *d) (3/2,4) e) (3/2,10)
5 - UFBA - Determine o valor de x que satisfaz à equação log2 (x-3) + log2 (x-2) = 1. Resp: 4
6 - UFBA - Existe um número x diferente de 10, tal que o dobro do seu logaritmo decimal excede de duas unidades o
logaritmo decimal de x-9. Determine x.
Resp: 90
7 - PUC-SP - O logaritmo, em uma base x, do número y = 5 + x/2 é 2. Então x é igual a:
a) 3/2 b) 4/3 c) 2 d)5 *e) 5/2
8 - PUC-SP - Se x+y = 20 e x - y = 5 , então log(x
2
- y
2
) é igual a:
a) 100 *b) 2 c) 25 d) 12,5 e) 1000
Sugestão: observe que x
2
- y
2
= (x - y) (x + y)
9 - Calcule o valor dos seguintes logaritmos:
a) b)
c) d)
e) f)
10 - Calcule o valor da incógnita "N" em cada exercício, aplicando a equivalência fundamental:
a) b) c) d)
11 - Calcule o valor da incógnita "a" em cada exercício, aplicando a equivalência fundamental:
a) b) c)](https://image.slidesharecdn.com/7463apostilamatematicaprofroberto-230301234649-780450f5/85/7463_APOSTILA_Matematica_Prof_Roberto-pdf-132-320.jpg)







![____________ _____________________________ MATEMÁTICA _________________________________ Prof. Roberto
__________________________________________________________________________________________________________________________
ATUALIZADO ATÉ MAIO/2012 www.CARREIRAPUBLICA.com.br (48) 4141-3220 4141-3222
139
29 - ( UEPG - PR ) A soma das raízes da equação 3
2x
- 12. 3
x
+ 27 = 0 pertence ao intervalo:
a. [ 10, 12 ] b. [ 0, 3 ] c. [ 1, 2 ] d. ( 10, 12 ) e. ( 1, 3 )
30 - ( UFPR ) Se 2
x
+ 2
-x
= 3, então o valor de 8
x
+ 8
-x
é:
a. 12 b. 18 c. 21 d. 24 e. 27
31 - ( FUVEST - SP ) Se 4
16
. 5
25
= . 10
n
, com 1 <10, então n é igual a:
a. 24 b. 25 c. 26 d. 27 e. 28
32 - ( FGV - SP ) A equação 4
x
+ 6
x
= 2.9
x
tem como solução o conjunto:
a. {1} b. {2} c. {3} d. {0} e. nda
33 - ( UECE ) Se 7
m
- 3
2n
= 1672 e - 3
n
= 22, então m
n
é igual a:
a. 16 b. 64 c. 128 d. 256 e. nda
34 - ( PUC - MG ) A expressão é igual a:
a. 2
x
b. 2
-x
c. 2
-3
d. 7
e. 8
35 - ( UFCE ) A soma das raízes da equação x
f(x)
= 1, onde f(x) = x
2
- 7x + 12, é igual a :
a. 5 b. 6 c. 8 d. 9 e. 10
36 - ( CESGRANRIO - RJ ) Os números inteiros x e y satisfazem 2
x+1
+ 2
x
= 3
y+2
- 3
y
. Então x é:
a. 0 b. 1 c. 2 d. 3 e. 4
18 ANÁLISE COMBINATÓRIA
Foi a necessidade de calcular o número de possibilidades existentes nos chamados jogos de azar que levou ao
desenvolvimento da Análise Combinatória, parte da Matemática que estuda os métodos de contagem. Esses estudos
foram iniciados já no século XVI, pelo matemático italiano Niccollo Fontana (1500-1557), conhecido como Tartaglia.
Depois vieram os franceses Pierre de Fermat (1601-1665) e Blaise Pascal (1623-1662).
A Análise Combinatória visa desenvolver métodos que permitam contar - de uma forma indireta - o número de
elementos de um conjunto, estando esses elementos agrupados sob certas condições
18.1 Fatorial
Notação : ( ! )
Def . : Denomina-se fatorial de um número positivo inteiro n ao produto
n ( n - 1 ) ( n - 2 ) ( n - 3 ) ( n - 4 ) ..... e anotamos n !](https://image.slidesharecdn.com/7463apostilamatematicaprofroberto-230301234649-780450f5/85/7463_APOSTILA_Matematica_Prof_Roberto-pdf-140-320.jpg)




![____________ _____________________________ MATEMÁTICA _________________________________ Prof. Roberto
__________________________________________________________________________________________________________________________
ATUALIZADO ATÉ MAIO/2012 www.CARREIRAPUBLICA.com.br (48) 4141-3220 4141-3222
144
18.4.4 Exercícios
1 ) Qual o número de permutações que podemos formar com a palavra PARALELA ?
2 ) Quantos anagramas podemos formar com a palavra MATEMÁTICA , quantos anagramas começam com a sílaba
MA.
3 ) Quantos anagramas podemos formar com a palavra :
a ) Diferente
b ) Determinação
c ) Elemento
4 ) Determine a quantidade de números distintos que podemos obter permutando-se os algarismos dos números a)
73.431 b) 343.434
5 ) Quantos anagramas podem ser formados com as letras da palavra ARAPONGA, de modo que a letra P ocupe
sempre o último lugar.
6 ) Usando uma vez a letra A, uma vez a letra B e ( n- 2 ) vezes a letra C, podemos formar 20 anagramas diferentes
com n letras em cada anagrama. Calcule n.
18.5 Combinação simples
13.5.1 Def . : Dado um conjunto de n elementos, chama-se de combinação simples de p elementos distintos a
todo subconjunto formado por p dos n elementos.
Um subconjunto é distinto de outro, quando em cada um dos dois houver pelo menos um dos p elementos distinto.
Fórmula
p
C = n ! .
n p!(n-p)!
Exemplos
1 ) Quantos subconjuntos de 3 elementos tem um conjunto de 5 elementos
Cn,p = n ! C5,3 = 5! . C5,3 = 10
p!(n-p)! 3! ( 5 - 3 )!
2 ) Dado um conjunto de 7 elementos calcule a quantidade de subconjuntos de 2 elementos.
C7,2 = 7 ! C7,2 = 21
2!(7-2)!
Combinação simples: Não ocorre a repetição de qualquer elemento em cada grupo de p elementos.
Fórmula: C(n,p) = n!/[(n-p)! p!]
Cálculo para o exemplo: C(4,2)=4!/[2!2!]=24/4=6
Exemplo: Seja C={A,B,C,D}, n=4 e p=2. As combinações simples desses 4 elementos tomados 2 a 2 são 6 grupos
que não podem ter a repetição de qualquer elemento nem podem aparecer na ordem trocada. Todos os
agrupamentos estão no conjunto:
Cs={AB,AC,AD,BC,BD,CD}
Combinação com repetição: Todos os elementos podem aparecer repetidos em cada grupo até p vezes.](https://image.slidesharecdn.com/7463apostilamatematicaprofroberto-230301234649-780450f5/85/7463_APOSTILA_Matematica_Prof_Roberto-pdf-145-320.jpg)
![____________ _____________________________ MATEMÁTICA _________________________________ Prof. Roberto
__________________________________________________________________________________________________________________________
ATUALIZADO ATÉ MAIO/2012 www.CARREIRAPUBLICA.com.br (48) 4141-3220 4141-3222
145
Fórmula: Cr(n,p)=C(n+p-1,p)
Cálculo para o exemplo: Cr(4,2)=C(4+2-1,2)=C(5,2)=5!/[2!3!]=10
Exemplo: Seja C={A,B,C,D}, n=4 e p=2. As combinações com repetição desses 4 elementos tomados 2 a 2 são 10
grupos que têm todas as repetições possíveis de elementos em grupos de 2 elementos não podendo aparecer o
mesmo grupo com a ordem trocada. De um modo geral neste caso, todos os agrupamentos com 2 elementos formam
um conjunto com 16 elementos:
Cr={AA,AB,AC,AD,BA,BB,BC,BD,CA,CB,CC,CD,DA,DB,DC,DD}
mas para obter as combinações com repetição, deveremos excluir deste conjunto os 6 grupos que já apareceram
antes, pois AB=BA, AC=CA, AD=DA, BC=CB, BD=DB e CD=DC, assim as combinações com repetição dos
elementos de C tomados 2 a 2, são:
Cr={AA,AB,AC,AD,BB,BC,BD,CC,CD,DD}
18.5.1 Exercícios
1 ) Quantas comissões com 4 alunos podemos formar numa classe de 20 alunos ? R. 4.845
2 ) Quantas comissões de 8 pessoas podemos formar com um grupo de 10 pessoas ? R. 45
3 ) Com 7 professores quantas comissões de 3 professores podemos formar ? R. 35
4 ) 12 pessoas participam de um jantar. No final eles se despedem com um aperto de mão. Quantos apertos de mão
serão dados no total ? R. 66
5 ) Com 4 homens e 6 mulheres, quantas comissões de 5 pessoas podemos formar se desejo que em cada
comissão esteja presente, pelo menos, um homem ?
6) Com 5 mulheres e 5 homens, quantas comissões de 4 pessoas podemos formar se desejo que cada comissão
tenha, no máximo, 2 mulheres ?
7 ) Calcule x na equação abaixo
2
4 C = 60 R. 6
x
8 ) Complete: x vale ......
4 3
C : C = 1 R. 7
x x
9 ) Calcule o numero de diagonais de um hexágono regular. R. 9
10 ) Calcule o número de diagonais de um icoságono. R. 170
11) De quantas maneiras podemos escalar um time de futebol de salão dispondo de 8 jogadores ?
12) Sobre uma reta marcam-se 8 pontos e sobre uma outra reta, paralela à primeira, marcam-se 5 pontos.Quantos
triângulos obteremos unindo 3 pontos quaisquer desses pontos ? R. 220
13) Uma empresa é formada por 6 sócios brasileiros e 4 japoneses. De quantos modos podemos formar uma diretoria
de 5 sócios, sendo 3 brasileiros e 2 japoneses ?
14) Um examinador dispõe de 6 questões de Álgebra e 4 de Geometria para montar uma prova de 4 questões.
Quantas provas diferentes ele pode montar usando 2 questões de Álgebra e 2 de Geometria ?
18.5.2 Exercícos resolvidos](https://image.slidesharecdn.com/7463apostilamatematicaprofroberto-230301234649-780450f5/85/7463_APOSTILA_Matematica_Prof_Roberto-pdf-146-320.jpg)