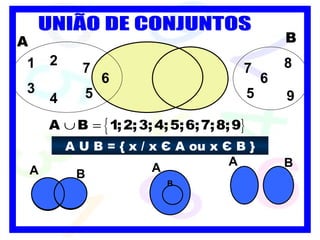
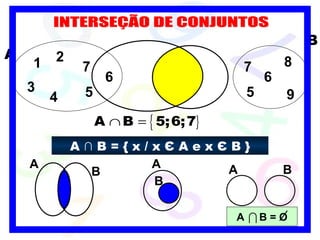
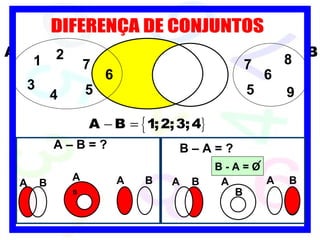
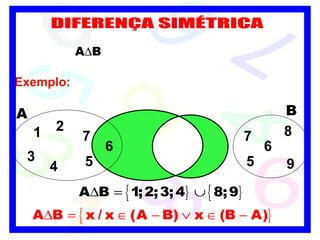
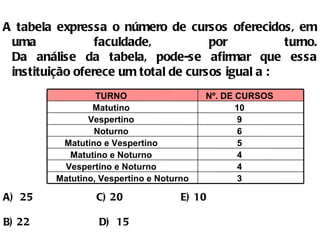
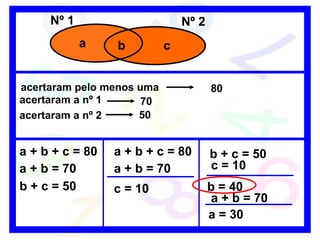
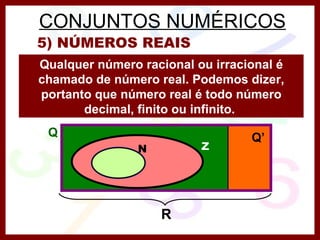
1) O documento discute conceitos básicos de conjuntos, incluindo formas de determinar conjuntos, diagramas de Venn e conjuntos especiais. 2) É explicado que um conjunto pode ser determinado através da listagem ou propriedade de seus elementos. 3) Conjuntos especiais como vazio, unitário, finito e infinito são definidos com exemplos.

1. Conjuntos

2. CONJUNTOS No estudo de Conjuntos, trabalhamos com alguns conceitos primitivos, que devem ser entendidos e aceitos sem definição.

3. DETERMINAÇÃO DE CONJUNTOS I) LISTAGEM Os elementos do conjunto estão dentro de duas chaves . Exemplos: A) O conjunto dos números pares maiores que 5 e menores que 20. A = { 6;8;10;12;14;16;18 }

4. II) Propriedade de Seus Elementos O conjunto é apresentado por meio de uma propriedade que sirva a todos os elementos do conjunto e somente a estes elementos. Exemplo: Seja A o conjunto das vogais do nosso alfabeto, então: A = {x / x é vogal do nosso alfabeto} A = {a , e , i , o , u }

5. DIAGRAMAS DE VENN Os elementos são representados por pontos interiores a uma linha fechada não entrelaçada. A M T 7 2 3 6 9 a e i o u 1 7 2 5 8 4 1 5

6. Exemplos : 1) Um conjunto formado por números inteiros entre 2 e 7. A = { 3 , 4 , 5 , 6 } A 3 4 5 6 2) Um conjunto formado por números Naturais pares e primos. A = { 2 } A 2 conjunto unitário A = { 2 }

7. CONJUNTOS ESPECIAIS CONJUNTO VAZIO Chamamos de conjunto vazio aquele formado por nenhum elemento. Representado por ou { } Exemplos: M = { números maiores que 9 e menores que 5 } = { } P = { x / }

8. CONJUNTO UNITÁRIO É o conjunto que tem um único elemento. Exemplos: F = { x / 2x + 6 = 0 } G = CONJUNTO FINITO É o conjunto com número limitado de elementos. Exemplos: E = { x / x é um número impar positivo menor que 10 } N = { x / x 2 = 4 } ;

9. CONJUNTO INFINITO É um conjunto com um número ilimitado de elementos. Exemplos: R = { x / x < 6 } S = { x / x é um número par } ;

10. RELAÇÃO DE PERTENÊNCIA Se um elemento pertence a um conjunto se usa o símbolo: Se um elemento não pertenece a um conjunto se usa o símbolo: Exemplo: Se M = {2;4;6;8;10} ... se lê 2 pertence ao conjunto M ... se lê 5 não pertence ao conjunto M

11. Exemplo: A= {a;b;c;d;e} n(A)= B= {x;x;x;y;y;z} n(B)= Não levamos em consideração a ordem, nem a repetição dos elementos. O conjunto {x; x; x; y; y; z } = { x; y; z }. Cardinal = nº de elementos. n(A) = nº de elem. de A 5 3 Atencão!

12. RELAÇÃO DE PERTENÊNCIA Exemplo: Se A = {2;4;6;{8};10} ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )

13. RELAÇÃO ENTRE CONJUNTOS INCLUSÃO Dizemos que o conjunto A está contido no conjunto B se A for uma parte de B . NOTAÇÃO : Se lê : A é subconjunto de B, A está contido em B , A é parte de B.

14. A A A A A 1 2 1 2 1 2 1 2 1 2

15. PROPRIEDADES: I ) Todo conjunto está contido em si mesmo. II ) O conjunto vazío está contido em qualquer conjunto.

16. Seja o conjunto A = { , 1 , 2, { 1 } }, então : ..... A 1 ..... A 2 ..... A { 1 } ..... A ..... A { , 1 , 2, { 1 } } ......... A { } ..... A 1 { } ..... A 2 { } ..... A { 1 } { } ..... A 1 , 2 { } ..... A

19. 7 6 5 5 6 UNIÃO DE CONJUNTOS A B 9 8 7 3 1 4 2 B A B A A B B A U B = { x / x Є A ou x Є B }

20. 7 6 5 5 6 A B 9 8 7 3 1 4 2 INTERSEÇÃO DE CONJUNTOS A B A A B B A B = O A ∩ B = { x / x Є A e x Є B }

21. 7 6 5 5 6 A B 9 8 7 3 1 4 2 DIFERENÇA DE CONJUNTOS B A – B = ? B – A = ? A B A B A B A B A A B B - A = O

22. 7 6 5 5 6 A B Exemplo: 9 8 7 3 1 4 2 DIFERENÇA SIMÉTRICA

23. A B A-B B-A A B

24. COMPLEMENTAR : C A B( complementar de B em relação a A ) Obs: C A B= A - B EX : A = { 1, 3 } e B = { 1 , 2 , 3 , 4 } C B A= { 2 , 4 } A B A B

25. Pág. 236

27. A B 4 5 E 6 7 1 2 3 { 3, 4, 5 }

29. (01) A pesquisa envolveu 500 pessoas . (02) 61 pessoas estavam matriculadas apenas em alongamento . (04) 259 pessoas estavam matriculadas em alongamento ou musculação . (08) 89 pessoas estavam matriculadas em pelo menos duas das atividades indicadas na tabela . (16) O número de pessoas matriculadas apenas em hidroginástica corresponde a 28,4% do total de pessoas envolvidas na pesquisa . ATIVIDADES N°. DE PESSOAS Alongamento 109 Hidroginástica 203 Musculação 162 Alongamento e hidroginástica 25 Alongamento e musculação 28 Hidroginástica e musculação 41 As três atividades 5 Outras atividades 115

32. a b c Nº 1 Nº 2 acertaram pelo menos uma 80 a + b + c = 80 acertaram a nº 1 70 a + b = 70 acertaram a nº 2 50 b + c = 50 a + b + c = 80 a + b = 70 c = 10 b + c = 50 c = 10 b = 40 a + b = 70 a = 30

34. OS CONJUNTOS NUMÉRICOS C R Q’ Q Z N ?

35. CONJUNTOS NUMÉRICOS 1) NÚMEROS NATURAIS Estes números foram criados pela necessidade de contar as coisas da natureza , por isso são chamados de números naturais. 1 2 3 4 N = { 1, 2, 3, 4, 5, ... } N = { 0, 1, 2, 3, 4, 5, ... }

37. CONJUNTOS NUMÉRICOS Entretanto...surgiu outro tipo de problema:“ Como dividir 3 vacas por 2 herdeiros ? “ Para resolver este tipo de problemas foram criados os números fracionários. 3) NÚMEROS RACIONAIS Q = Z  { números fracionários } N Z Q N Z Q

39. (01) Se x = 0,666... , y = -1,333... e z = 12,444..., então = 6,222.... .

40. CONJUNTOS NUMÉRICOS Ao aplicar o Teorema de Pitágoras para determinar a medida do comprimento da diagonal de um quadrado de lado unitário, não conseguimos encontrar um número racional para essa medida. 4) NÚMEROS IRRACIONAIS Ex.: N Z Q Q’

41. CONJUNTOS NUMÉRICOS Qualquer número racional ou irracional é chamado de número real. Podemos dizer, portanto que número real é todo número decimal, finito ou infinito. 5) NÚMEROS REAIS N Z Q Q’ R

43. Símbolos de exclusão: * Exclui o zero. + Exclui os negativos. - Exclui os positivos. A * = números não nulos. A + = A + = números não negativos. A -- = números não positivos. A * + = números positivos. A * -- = números negativos.

44. v F F v v v F v

45. A = { 0, 2 ,4 ,6 ,8, 10, ...} B = { -1, 0, 1 ,2 ,3 ,4 ,5 } C = { 0, 1 ,2 ,3 ,4 } B X 2 4 -1 1 3 0 5

46. Intervalos [a; b] = { x Є R/ a ≤ x ≤ b } = a b ]a; b[ = { x Є R/ a < x < b } = a b [a; b[ = { x Є R/ a ≤ x < b } = a b ]a; b] = { x Є R/ a < x ≤ b } = a b [a; + ∞[ = { x Є R/ x ≥ a } = a ]- ∞; a[ = { x Є R/ x < a } = a