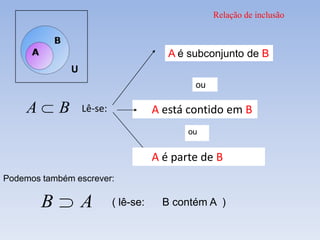
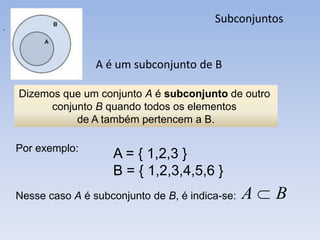
O documento apresenta os conceitos básicos de conjuntos e operações entre conjuntos. Introduz conjuntos como coleções de objetos e apresenta formas de representá-los. Explica termos como conjunto unitário, conjunto vazio e subconjuntos. Detalha operações como união, intersecção, diferença e complementar entre conjuntos. Por fim, exemplifica subconjuntos importantes dos números naturais.

1. CONJUNTOS
e
CONJUNTOS NUMÉRICOS
PARTE - 01/04
MATEMÁTICA
Prof. Carlos Eduardo (Zico)
http://www.zicoprofessor.blogspot.com
FEVEREIRO - 2012

2. CONJUNTOS
CONCEITOS PRIMITIVOS.
De forma intuitiva associamos um conjunto a uma coleção de objetos. Toda
coleção de objetos , animais, pessoas, ou coisas constitui um conjunto.
A idéia de conjunto é a mesma de coleção.
Os objetos são os elementos do conjunto.
Vejamos alguns exemplos:
1o) Uma coleção de livros escolares é um conjunto; e cada livro é um elemento
desse conjunto.
2o) Os alunos do 1ºA formam um conjunto; e cada aluno é um elemento desse
conjunto.
2o) Um time de voleibol é um conjunto; e cada atleta do time é um elemento
desse conjunto.

3. REPRESENTAÇÕES DE UM CONJUNTO:
1) Por extenso ou escrita por extenso ou escrita por extensão ou representação tabular.
Enumeram-se seus elementos, escrevendo-os entre chaves e separando-os por vírgulas.
Exemplos:
Vogais do nosso
alfabeto.
A a, e, i, o, u
Números naturais
ímpares.
B 1,3,5,... Números naturais
menores que 6.
C 0,1,2,3,4,5

4. REPRESENTAÇÕES DE UM CONJUNTO:
2) Por compreensão ou escrita por compreensão ou por uma propriedade característica.
A = { x/x é vogal do nosso alfabeto } A a, e, i, o, u
B = { x/x é número natural ímpar } B 1,3,5,...
C = { x/x é número natural menor que 6 }
C x IN / x 6
C 0,1,2,3,4,5
C x IN / 0 x 5

5. REPRESENTAÇÕES DE UM CONJUNTO:
3) Por figuras ou graficamente usando diagramas ou diagrama de Venn.
e A
i C
2
a
u
0 4
o
1
5
3

6. Terminologia – Tipos de conjuntos
Conjunto unitário: É aquele que possui um único
elemento.
Exemplos:
A x IN / 3 x 5 é o mesmo que A 4
B 7 é o mesmo que, por exemplo: B x IN / 7 x 8
ou, é o mesmo que, por exemplo: B x IN / 6 x 8
C x IN / x 1 é o mesmo que C 0

7. Conjunto vazio: Todo conjunto também possui como
subconjunto o conjunto vazio representado por:
OU Ø
Podemos mostrar isto supondo que se o conjunto vazio não
está contido no conjunto em questão, então o conjunto vazio
deve possuir um elemento ao menos que não pertença a este
conjunto. Como o conjunto vazio não possui elementos, isto
não é possível. Como todos os conjuntos vazios são iguais uns
aos outros, é permissível falar de um único conjunto sem
elementos.
Exemplos: C x IN / 4 x 5
A
B D x IN / x 0

8. Relação de inclusão
Relação de pertinência
Se a é um elemento de A, nós podemos dizer que o elemento a
pertence ao conjunto A e podemos escrever a A
Se a não é um elemento de A, nós podemos dizer que o elemento a
não pertence ao conjunto A e podemos escrever a A
Exemplos:
16 Z c a, b, c, d , e, f , g , h
1 c a, e, i, o, u
Z
4

9. Relação de inclusão
A é subconjunto de B
U
ou
A B Lê-se: A está contido em B
ou
A é parte de B
Podemos também escrever:
B A ( lê-se: B contém A )

10. Subconjuntos
.
A é um subconjunto de B
Dizemos que um conjunto A é subconjunto de outro
conjunto B quando todos os elementos
de A também pertencem a B.
Por exemplo:
A = { 1,2,3 }
B = { 1,2,3,4,5,6 }
Nesse caso A é subconjunto de B, é indica-se: A B

11. A é um subconjunto de B
Deve-se reparar que B é subconjunto de si mesmo; os
subconjuntos de B que não são iguais a B são
chamados subconjuntos próprios.
Nota: O conjunto vazio ou Ф (phi), é um
{ },
subconjunto de todos os conjuntos.

12. Operações entre conjuntos
União
União de A e B (em azul )
A união de dois conjuntos A e B é um conjunto que
contém todos os elementos de A, todos os elementos
de B, e nada mais além disso. Ou então: Dado um
universo U e dois conjuntos A e B, chama-se
união de A com B ao conjunto cujos elementos
pertencem pelo menos ao conjunto A ou
ao conjunto B.
“Matematicamente”: A B x U/x A x B

13. Exemplo: Dados os conjuntos A a, e, i , B o, u ,
C 2,3,4,5 e D 1,3,5 , determine
A B e C D
Resolução: A B a, e, i, o, u
C D 1,2,3,4,5
Respostas: A B a, e, i, o, u
C D 1,2,3,4,5

14. Notas sobre União de conjuntos:
•A união de um conjunto A , qualquer que seja, com o
conjunto vazio é igual ao próprio conjunto A , isto é:
A A
•Também deve ser observado que a operação de
união é comutativa, ou seja,
A B C A B C A C B

15. Intersecção
Intersecção de A e B
(em azul mais escuro)
A intersecção de dois conjuntos A e B é o conjunto de
elementos que pertencem aos dois conjuntos. Ou então:
Dados dois conjuntos A e B , pertencentes a um
universo U, chama-se intersecção de A com B ao
conjunto cujos elementos pertencem tanto a A quanto a B.
“Matematicamente”: A B x U/x A x B
ou A B x U/x A e x B

16. Exemplos:
1) Dados os conjuntos C 2,4,6 e D 2,3,4,5 , determine
C D.
Resolução: C D 2,4
Resposta: C D 2,4

17. 2) Dados os conjuntos A a, e, i e B o, u , determine
A B
Resolução: A B
Resposta: A B

18. 3) Dados os conjuntos E 5,6,7,8,9,10,11,12,13,14,15,16
e F IN , determine E F
Resolução: E F E
Resposta: E F E

19. Diferença
Diferença A menos B (em azul mais escuro)
Dado um universo U ao qual pertencem dois
conjuntos A e B:
- chama-se diferença de A menos B ao conjunto de
elementos que pertencem a A e não pertencem a B;
- chama-se de diferença de B menos A ao conjunto
de elementos que pertencem a B e não pertencem a A.
“Matematicamente”: A B x U/x A x B
B A x U/x B x A

20. Por exemplo, o conjunto definido pela diferença entre
os números inteiros e números naturais não nulos é
igual ao conjunto Z- (números inteiros não-positivos):
*
Z ..., 2, 1,0,1,2,... IN 1,2,3,...
Z IN * Z_ ..., 2, 1,0
•A subtração de um conjunto A menos um conjunto vazio
é igual ao próprio conjunto A, isto é,
A-{ }=A

21. Complementar
Complementar de B em relação a A
(em azul mais escuro)
Dado um universo U, diz-se complementar de um
conjunto A, em relação ao universo U, o conjunto que
contém todos os elementos presentes no universo e
que não pertençam a A. Também define-se complementar
para dois conjuntos, contanto que um deles seja subconjunto
do outro. Nesse caso, diz-se, por exemplo, complementar
de B em relação a A (sendo B um subconjunto de A) B
— é o complementar relativo — e usa-se o símbolo C A
B
“Matematicamente”: C A x A/ x B

22. D
Exemplo: Dados os conjuntos A e D, determine C A
.A = { 3,4,9,{10,12},{25,27} } e D = { {10,12} }
D
Resolução: C A 3,4,9, 25,27
D
Obs: C A A D
Note no exemplo acima esta operação.

23. SUBCONJUNTOS importantes dos NATURAIS
1º) Naturais Não Nulos: IN * = {1, 2, 3, 4, 5, 6, 7,...}
2º) Naturais Pares: INP = { 0, 2, 4, 6,..., 2n, ...} , com n IN
3º) Naturais Ímpares: IN I = { 1, 3, 5, 7,..., 2n+1, ...} , com n IN
4º) Números Primos: P = { 2, 3, 5, 7, 11, 13, 17, 19, ...}

24. Números Naturais na reta real
Veja onde estão os
NÚMEROS NATURAIS
na reta real
…………………….
3 2 1
0 1 2 3 4 5 6 7
0 1 2 3 4 5 6 7
Não esquecer, por exemplo: 2, 7 e 2 não são números naturais
“Os números naturais são aqueles pintandos em vermelhos”.

25. FIM da PARTE 01/04
VEJA a PARTE 02/04
CONJUNTOS
e
CONJUNTOS NUMÉRICOS
PARTE - 01/04
MATEMÁTICA
Prof. Carlos Eduardo (Zico)
http://www.zicoprofessor.blogspot.com
FEVEREIRO - 2012