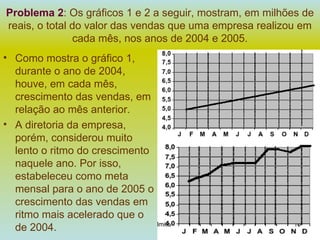
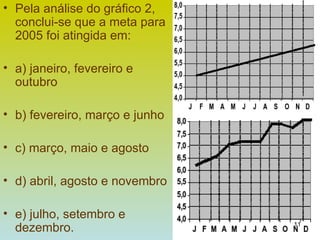
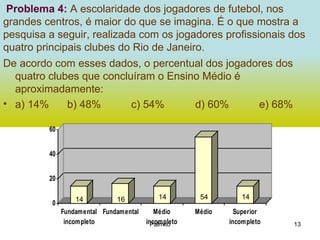
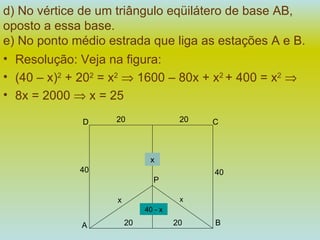
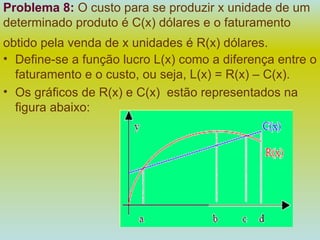
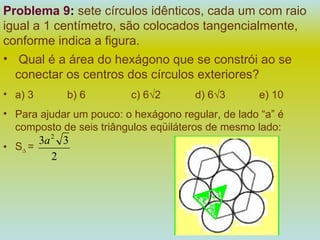
1) O documento apresenta 10 problemas de matemática do ENEM com questões sobre probabilidade, porcentagem, geometria e análise de gráficos. 2) As competências avaliadas pelo ENEM incluem interpretar textos, fenômenos e solucionar problemas matemáticos. 3) As habilidades mais relevantes para a matemática são identificar variáveis, compreender gráficos e calcular probabilidades.

1. 1x8 + 1= 9 12x8 + 2 = 98 123x8 + 3 = 987 1234x8 + 4 = 9876 12345x8 + 5 = 98765 123456x8 + 6 = 987654 1234567x8 + 7 = 9876543 12345678x8 + 8 = 98765432 123456789x8 + 9 = 987654321 Matemática Enem

2. Cada questão do ENEM testa, no mínimo, três das cinco competências exigidas. As competências mais diretamente ligadas à Matemática são: I) Dominar linguagens : saber interpretar textos, gráficos, tabelas,quadros, ilustrações,esquemas e qualquer forma de comunicação escrita em papel. II) Compreender e interpretar fenômenos : capacidade de interligar as disciplinas entre si e conectar o conteúdo aprendido com o mundo que nos cerca. III) Solucionar problemas : é preciso interpretar o fato (competência I) e ter as informações corretas sobre o fenômeno (competência II) para tomar a decisão acertada e resolver a proposta.

3. Dentre as 21 habilidades, das quais aparecem pelo menos três em cada questão, as mais diretamente ligadas à Matemática são: 1) Identificar variáveis 2) Compreender gráficos 3) Identificar tendências 4) Transformar linguagens 5) Conhecer as formas geométricas 6) Calcular probabilidades.

4. Problema 1 : Um time de futebol amador ganhou uma taça ao vencer um campeonato. Os jogadores decidiram que o prêmio seria guardado na casa de um deles. Como todos queriam ficam com o troféu, travou-se o seguinte diálogo: Pedro (camisa 6) : Nós somos onze jogadores e nossas camisas estão numeradas de 2 a 12. Tenho 2 dados com faces numeradas de 1 a 6. Vou jogar os dois dados simultaneamente e somar os resultados das duas faces. Os resultados podem variar de 2 (1+1) até 12 (6+6). Quem tiver a camisa com o resultado, guardará o troféu em sua casa.

5. Tadeu (camisa 2) : Não sei não... Acho que Pedro está querendo levar vantagem com esta proposta. Ricardo(camisa 12) : Você pode estar certo. O Pedro pode ter mais chances de ganhar do que nós dois juntos... Desse diálogo conclui-se que: a) Tadeu e Ricardo estavam equivocados, pois a probabilidade de ganhar a guarda da taça era a mesma para todos. b) Tadeu tinha razão e Ricardo estava equivocado, pois, juntos, tinham mais chance de ganhar a guarda da taça do que Pedro.

6. c) Tadeu tinha razão e Ricardo estava equivocado, pois, juntos, tinham a mesma chance de ganhar a guarda da taça do que Pedro. d) Tadeu e Ricardo tinham razão, pois os dois juntos tinham menos chances de ganhar a guarda da taça do que Pedro e) Não é possível saber qual dos dois jogadores tinha razão, por se tratar de um resultado probabilístico, que depende exclusivamente da sorte.

7. Na tabela a seguir, estão colocadas todas as somas possíveis que podem aparecer no lançamento de dois dados distinguíveis: A probabilidade da soma ser seis (Pedro ficar com a taça) é 5/36. Os dois outros, juntos, teriam probabilidade igual a 2/36. A resposta correta é a (d) Dado 1 Dado 2 12 11 10 9 8 7 6 11 10 9 8 7 6 5 10 9 8 7 6 5 4 9 8 7 6 5 4 3 8 7 6 5 4 3 2 7 6 5 4 3 2 1 6 5 4 3 2 1

8. A BELEZA DOS NÚMEROS

9. 9x9 + 7 = 88 98x9 + 6 = 888 987x9 + 5 = 8 888 9 876x9 + 4 = 88 888 98 765x9 + 3 = 888 888 987 654x9 + 2 = 8 888 888 9 876 543x9 + 1 = 88 888 888 98 765 432x9 + 0 = 888 888 888 987 654 321x9 – 1= 8 888 888 888 9 876 543 210x9 – 2 = 88 888 888 888

10. Problema 2 : Os gráficos 1 e 2 a seguir, mostram, em milhões de reais, o total do valor das vendas que uma empresa realizou em cada mês, nos anos de 2004 e 2005. Como mostra o gráfico 1, durante o ano de 2004, houve, em cada mês, crescimento das vendas, em relação ao mês anterior. A diretoria da empresa, porém, considerou muito lento o ritmo do crescimento naquele ano. Por isso, estabeleceu como meta mensal para o ano de 2005 o crescimento das vendas em ritmo mais acelerado que o de 2004.

11. Pela análise do gráfico 2, conclui-se que a meta para 2005 foi atingida em: a) janeiro, fevereiro e outubro b) fevereiro, março e junho c) março, maio e agosto d) abril, agosto e novembro e) julho, setembro e dezembro.

12. Problema 3: As 23 alunas de uma turma que completou o Ensino Médio há 10 anos encontraram-se em uma reunião comemorativa. Várias delas haviam se casado e tido filhos. A distribuição das mulheres, de acordo com o números de filhos, é mostrado no gráfico ao lado. Um prêmio foi sorteado entre todos os filhos dessas ex-alunas. A probabilidade de que a criança sorteada tenha sido um filho(a) único(a) é: a) 1/3 b) 1/4 c) 7/15 d) 7/23 e) 7/25

13. Problema 4: A escolaridade dos jogadores de futebol, nos grandes centros, é maior do que se imagina. É o que mostra a pesquisa a seguir, realizada com os jogadores profissionais dos quatro principais clubes do Rio de Janeiro. De acordo com esses dados, o percentual dos jogadores dos quatro clubes que concluíram o Ensino Médio é aproximadamente: a) 14% b) 48% c) 54% d) 60% e) 68% 14 16 14 54 14

14. Dos 112 jogadores, 54 + 14 = 68 concluíram o Ensino Médio, e portanto, a resposta correta é 68/112 ≈ 60 % (D) Problema 5: Quatro estações distribuidoras de energia A, B, C e D estão dispostas como os vértices de um quadrado de 40 km de lado. Deseja-se construir uma estação central que seja ao mesmo tempo eqüidistante das estações A e B, e da estrada (reta) que liga as estações C e C. A nova estação deve ser localizada: a) no centro do quadrado b) na perpendicular à estrada que liga C e D passando por seu ponto médio, a 15 km dessa estrada c) na perpendicular à estrada que liga C e C passando por seu ponto médio, a 25 km dessa estrada

15. d) No vértice de um triângulo eqüilátero de base AB, oposto a essa base. e) No ponto médio estrada que liga as estações A e B. Resolução: Veja na figura: (40 – x) 2 + 20 2 = x 2  1600 – 80x + x 2 + 400 = x 2  8x = 2000  x = 25 40 - x x x A B 20 20 P x 40 40 C D 20 20

16. A BELEZA DOS NÚMEROS

17. 1x1= 1 11x11= 121 111x111 = 12321 1111x1111= 1234321 11111x11111 = 123454321 111111x111111= 12345654321 1111111x1111111= 1234567654321 11111111x11111111 = 123456787654321

18. Prefixos  múltiplos (antepostos ao nome de unidades usuais de medidas) Unidade: grama (g), litro (l), hertz (hz), watt (w), byte (b) Deca: (da) 10 vezes 10 1 Hecto: (h) 100 vezes 10 2 Quilo: (k) 1000 vezes 10 3 Mega: (M) 1milhão vezes 10 6 Giga: (G) 1bilhão vezes 10 9 Tera: (T) 1trilhão vezes 10 12 Peta: (P) 1 quadrilhão vezes 10 15 Exa: (E) 1 quinqüilhão vezes 10 18 Zetta: (Z) 1 hexilhão 10 21 Yotta: (Y) 1 heptilhão 10 24

19. Prefixos  sub-múltiplos antepostos ao nome de unidades usuais de medidas Unidade: grama (g); litro (l), hertz (hz), watt (w), ... Deci: (d) décima parte 10 -1 centi: (c) centésima 10 -2 mili: (m) milésima parte 10 -3 micro:  milionésima parte 10 -6 nano: (n) bilionésima parte 10 -9 pico: (p) trilionésima parte 10 -12 femto: (f) quadrilionésima parte 10 -15 atto: (a) quinqüilionésima parte 10 -18 zeptto: (z) hexilionésima parte 10 -21 yocto: (y) heptilionésima parte 10 -24

20. Problema 6: Quem é maior: 2 30.000 ou 3 20.000 ? a) 2 30.000 b) 3 20.000 c) Os dois números são iguais. d) Não é possível calcular o valor exato de potências com expoentes tão grandes. e) Só é possível a comparação de potências que possuam a mesma base. Temos: 2 30.000 = (2 3 ) 10.000 = 8 10.000 3 20.000 = (3 2 ) 10.000 = 9 10.000 Assim, 3 20.000 > 2 30.000 . Alternativa (b).

21. Problema 7: Cada um dos cartões abaixo tem de um lado um número e do outro lado, uma letra. A B 2 3 Alguém afirmou que todos os cartões que têm uma vogal numa face têm um número par na outra. Para verificar se tal afirmação é verdadeira: a) É necessário virar todos os cartões. b) É suficiente virar o primeiro e o último cartão. c) É suficiente virar os dois cartões do meio. d) É suficiente virar os dois primeiros cartões. e) N. d. a.

22. Problema 8: O custo para se produzir x unidade de um determinado produto é C(x) dólares e o faturamento obtido pela venda de x unidades é R(x) dólares. Define-se a função lucro L(x) como a diferença entre o faturamento e o custo, ou seja, L(x) = R(x) – C(x). Os gráficos de R(x) e C(x) estão representados na figura abaixo:

23. Então: a) Esta empresa nunca terá lucro porque o custo é sempre crescente e a receita não. b) Esta empresa terá lucro enquanto a receita R estiver crescendo, ou seja, para x < b. c) Esta empresa terá lucro para a < x < c. d) Esta empresa terá lucro para 0 < x < a e c < x < d. e) N. d. a

24. 1x9 + 2 = 11 12x9 + 3 = 111 123x9 + 4 = 1 111 1234x9 + 5 = 11 111 12345x9 + 6 = 111 111 123456x9 + 7 = 1 111 111 1234567x9 + 8 = 11 111 111 12345678x9 + 9 = 111 111 111 123456789x9 +10 = 1 111 111 111

25. Problema 9 : sete círculos idênticos, cada um com raio igual a 1 centímetro, são colocados tangencialmente, conforme indica a figura. Qual é a área do hexágono que se constrói ao se conectar os centros dos círculos exteriores? a) 3 b) 6 c) 6√2 d) 6√3 e) 10 Para ajudar um pouco: o hexágono regular, de lado “a” é composto de seis triângulos eqüiláteros de mesmo lado: S ∆ =

26. Problema 10: Em um dado, a soma dos pontos de duas faces opostas é sempre igual a 7. Duas pessoas estão sentadas à mesa, frente a frente, e entre elas está colocado um grande dado sobre a mesa. Cada uma das pessoas vê três faces do dado, sendo que a face superior é vista simultaneamente pelas duas pessoas. Se a soma dos números nas faces vistas por uma das pessoas é 7 e a soma dos números nas faces vistas pela outra pessoa é 11, então o número na face que está em contato com a mesa é igual a: a) 2 b) 3 c) 4 d) 5 e) 6

27. Resolução: Sejam x, y ,z as três faces vistas por uma das pessoas, sendo z, t, w as três faces vistas pela outra pessoa. Seja ainda z´ a face voltada para a mesa, e oposta da face z, que é vista simultaneamente pelas duas pessoas. Temos x + y = 7 – z e t + w = 11 – z. x + y + z + t + w + z´ = 21 Assim, 7 – z + z + 11 – z + z´ = 21 z´ - z = 3 e z` + z = 7. Logo, z´ = 5.