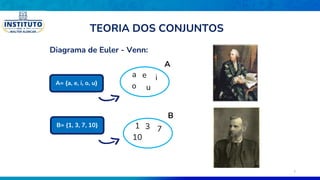
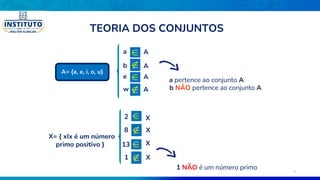
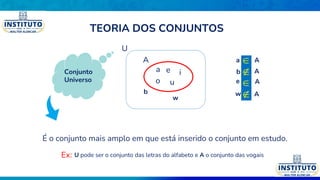
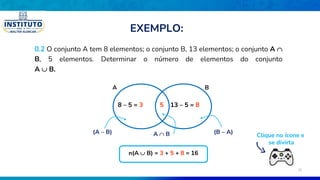
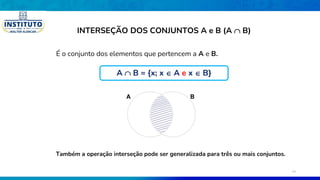
O documento aborda os fundamentos da teoria dos conjuntos, definindo conjuntos, seus elementos e propriedades. Conceitos como união, interseção, diferença entre conjuntos e subconjuntos são explorados, juntamente com exemplos práticos. Além disso, o texto discute notações e diagramas relacionados à teoria dos conjuntos, como o diagrama de Venn.

1. TEORIA DOS
CONJUNTOS
AULA 01
1

2. TEORIA DOS CONJUNTOS
Conjuntos:Lista, coleção, agrupamento ou classe de objetos bem definidos.
Objetos:Qualquer coisa: números, pessoas, letras, rios, etc...
Elementos ou membros de um conjunto
Exemplos : 1. Os números 1, 3, 7 e 10
2. As vogais do alfabeto: a, e, i, o e u
3. As pessoas que habitam a Terra
4. Os alunos que faltaram à aula
5. Os times de futebol do estado do Ceará
2

3. Conjunto  agrupamento, coleção
Conjunto dos times de futebol para os quais os alunos de uma classe torcem:
Real Madri, Barcelona, Manchester City  finito
Conjunto dos dias em que uma pessoa pratica natação:
segunda-feira, quarta-feira, sexta-feira  finito
Conjunto dos números pares:
0, 2, 4, 6, 8...  infinito
NOÇÕES BÁSICAS
3

4. NOTAÇÃO:
Elementos:
Letras maiúsculas: A, B, X, Y, ...
Conjuntos:
Letras minúsculas: a, b, x, y, ...
NOÇÕES BÁSICAS
Descrição pela citação
dos elementos:
A= {a, e, i, o, u}
B= {1,3,7,10}
X= {2,4,6,8}
Descrição por
propriedade:
A= {x | x é uma pessoa que
habita a Terra}
B= {x | x é um rio do Brasil}
X= {x | x é um número primo
positivo}
4

5. Diagrama de Euler - Venn:
A
a e i
o u
B
1 3 7
10
A= {a, e, i, o, u}
B= {1, 3, 7, 10}
TEORIA DOS CONJUNTOS
5

6. X= { xIx é um número
primo positivo }
a  A
b  A
e  A
w  A
a pertence ao conjunto A
b NÃO pertence ao conjunto A
2  X
8  X
13  X
1  X
1 NÃO é um número primo
A= {a, e, i, o, u}
TEORIA DOS CONJUNTOS
6

7. Conjunto
Universo
 A
b  A
e  A
w A
A
a e i
o u
b
w
U
a
É o conjunto mais amplo em que está inserido o conjunto em estudo.
Ex: U pode ser o conjunto das letras do alfabeto e A o conjunto das vogais
TEORIA DOS CONJUNTOS
7

8. Conjunto Unitário : Aquele que possui um único elemento.
A = { 2 }
B
a
Saiba mais clicando aqui!
TEORIA DOS CONJUNTOS
8

9. A = { x I x é um habitante da Terra com mais de 200 anos }
Conjunto Vazio : Aquele que não possui nenhum elemento
A = { }
OBS: Conjunto unitário da letra norueguesa Ǿ
Não representa um conjunto vazio
A = Ǿ
ou A = Ǿ
A = {Ǿ }
TEORIA DOS CONJUNTOS
9

10. Conjuntos Iguais : Dois conjuntos são iguais se, e somente se, possuem os
mesmos elementos
A = { a, b, c, d, e } B = { a, b, c, d, e } A = B
Ex:
  
A B x x A x B
     
A = B ⇔ ( ∀x ) (x ∈ A ⇔ x ∈ B)
TEORIA DOS CONJUNTOS
10

11. A = { 1, 2, 3, 4 } B = { 3, 1, 4, 2 } A = B
C = { 5, 6, 5, 7 } D = { 7, 5, 7, 6 } C = D
A
1 5
7
9
10
B
1 5
7
8
10
A ≠ B
TEORIA DOS CONJUNTOS
11

12. Subconjuntos : A é subconjunto de B se cada elemento do conjunto A
é também elemento do conjunto B .
A é subconjunto de B
A 1 5
7
9
10
B
U
A é subconjunto de B
A está contido em B
B contém A
TEORIA DOS CONJUNTOS
⇔ ( ∀x ) (x ∈ A ⇒ x ∈ B)
A ⊂ B
B ⊃ A
12

13. A a
b
d
c
e
B
U
C não é subconjunto de D
A está contido em B
B contém A
C = { 5, 6, 3, 2 } D = { 3, 5, 7, 6 }
A é subconjunto de B
C não está contido em D
TEORIA DOS CONJUNTOS
A ⊂ B
B ⊃ A
C ⊄ D
13

14. O conjunto vazio é subconjunto de qualquer conjunto:
OBS :
Qualquer conjunto é subconjunto dele mesmo:
A A
 A A

TEORIA DOS CONJUNTOS
∅ ⊂ A A ⊃ ∅
A ⊂ A A ⊃ A
14

15. Conjunto das Partes: Chamamos de conjunto das Partes do conjunto A e
representamos por P(A), o conjunto de todos os
subconjuntos do conjunto A.
C = { x, y, z } P(A) = { Ǿ, {x}, {y}, {z}, {x, y}, {x, z}, {y. z}, {x, y, z} }
n(A) = número de elementos de A = 3
n(P(A)) = número de elementos do conjunto das Partes de A = 2n(A) = 23 = 8
n(P(A)) = 2n(A)
TEORIA DOS CONJUNTOS
15

16. NÚMERO DE ELEMENTOS DA UNIÃO DE CONJUNTOS:
Existe uma relação importante que envolve a quantidade de elementos dos
seguintes conjuntos finitos: A, B, A  B e A  B.
Observe:
• n(A  B) = número de elementos da união
• n(A) = número de elementos do conjunto A
• n(B) = número de elementos do conjunto B
• n(A  B) = número de elementos da interseção
n(A  B) = n(A) + n(B) – n(A  B)
16

17. 0.1 Sejam A = {1, 2, 3, 4, 5, 6} e B = {4, 5, 6, 7, 8}, temos:
• A  B = {1, 2, 3, 4, 5, 6, 7, 8}
• A  B = {4, 5, 6}
Podemos comprovar que:
n(A  B) = n(A) + n(B) – n(A  B)
B
A
2
1 4
6
5
3
8
7
EXEMPLO:
8 = 6 + 5 – 3
17

18. 0.2 O conjunto A tem 8 elementos; o conjunto B, 13 elementos; o conjunto A 
B, 5 elementos. Determinar o número de elementos do conjunto
A  B.
B
A
5
8 – 5 = 3 13 – 5 = 8
n(A  B) = 3 + 5 + 8 = 16
(A – B) (B – A)
A  B Clique no ícone e
se divirta
EXEMPLO:
18

19. 03. Numa turma de 42 alunos, o professor perguntou: “Quem é torcedor do Grêmio?” 36
levantaram o braço. A seguir, perguntou: “Quem é nascido em Porto Alegre?” 28
levantaram o braço. Sabendo que nenhum aluno deixou de levantar o braço, vamos
determinar quantos alunos são gremistas e Porto-alegrenses.
P
G
x
36 – x 28 – x
36 – x + x + 28 – x = 42
(G – P) (G – P)
G  P
⇒ 64 – x = 42 ⇒ x = 22
EXEMPLO:
19

20. 20

21. A partir de dois conjuntos conhecidos, A e B, podemos obter outros
conjuntos, operando com os conjuntos dados.
Definimos as operações a seguir:
I. União;
II. Interseção;
III. Diferença;
OPERAÇÕES COM CONJUNTOS
21

22. É o conjunto dos elementos que pertencem ou a A, ou a B ou a
ambos os conjuntos.
B
A
Podemos generaliza a operação união para três ou mais conjuntos.
UNIÃO DOS CONJUNTOS A e B (A  B)
A  B = {x; x  A ou x  B}
22

23. 04. Dados os conjuntos A = {0, 1, 2, 3, 4}, B = {1, 3, 5, 7} e
C = {5, 6, 7, 8, 9}, vamos obter:
a) A  B.
b) A  B  C.
a) A  B = {0, 1, 2, 3, 4, 5, 7}
b) A  B  C = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
No caso de três ou mais conjuntos, podemos escrever
A  B  C = (A  B)  C = A  (B  C).
EXEMPLO:
23

24. É o conjunto dos elementos que pertencem a A e B.
B
A
Também a operação interseção pode ser generalizada para três ou mais conjuntos.
INTERSEÇÃO DOS CONJUNTOS A e B (A  B)
A  B = {x; x  A e x  B}
24

25. 05. Dados os conjuntos A = {0, 1, 5}, B = {0, 2, 5, 7}, C = {4, 6, 7, 9} e
D = {0, 1, 6}, vamos obter:
a) A  B.
b) A  C.
c) A  B  D.
a) A  B = {0, 5}
b) A  C = Ø
Logo, A e C são disjuntos.
c) A  B  D = {0}
EXEMPLO:
25

26. DIFERENÇA DOS CONJUNTOS A E B (A – B E B – A )
É o conjunto dos elementos que pertencem ao primeiro conjunto, mas não
pertencem ao segundo.
B
A
A – B = {x; x  A e x  B}
26

27. É o conjunto dos elementos que pertencem ao primeiro conjunto, mas não
pertencem ao segundo.
B
A
DIFERENÇA DOS CONJUNTOS A e B (A – B e B – A )
B – A = {x; x  B e x  A}
27

28. 06. Dados os conjuntos:
A = {1, 2, 3, 4, 5}, B = {2, 4, 6}, vamos obter:
a) A – B.
b) B – A.
a) A – B = {1, 2, 3, 4, 5} – {2, 4, 6} =
b) B – A = {2, 4, 6} – {1, 2, 3, 4, 5} =
Em geral A – B ≠ B – A.
{1, 3, 5}
{6}
EXEMPLO:
28

29. 07. Se A = {x natural, menor que 10 / x é par} e B = {x natural, menor
que 10 / x é primo}.
Determine A  B, A  B, A – B e B – A.
A = {0, 2, 4, 6, 8} B = {2, 3, 5, 7}
A  B = {0, 2, 3, 4, 5, 6, 7, 8}
A  B = {2} B
A
2
0
4 6
8
3
5
7
A – B = {0, 4, 6, 8}
B – A = {3, 5, 7}
EXEMPLO:
29

30. A = {0, 1, 2, 3, 4, 5, ...}
B = {0, 2, 4, 6, 8, 10, ...}
Complementar do conjunto A em relação a B é o conjunto formado
pelos elementos que pertencem a A e não pertencem a B.
COMPLEMENTAR DE UM CONJUNTO
30

31. No caso em que o conjunto B está contido no conjunto A (B ⊂ A), a diferença A
– B pode ser chamada, também, complementar de B em relação a A (∁AB).
A B A – B
O complementar de A em relação a um dado universo pode ser
representado, simplesmente por A.
COMPLEMENTAR DE UM CONJUNTO
B ⊂ A ⇒ A – B = ∁AB
31

32. 08. Dados os conjuntos
X = {1, 2, 4}, Y = {1, 2, 3, 4, 5}, X ⊂ Y.
Obter ∁YX.
∁YX = Y – X = {1, 2, 3, 4, 5} – {1, 2, 4} = {3, 5}
Se A = {x  ℝ; x > 2}, A está contido no universo ℝ. Obter ∁A.
∁A = A = {x  ℝ; x ≤ 2}
EXEMPLO:
32

33. 09. Se A = {a, b, c, d, e} e B = {d, e, f, g} estão contidos no
universo
U = {a, b, c, d, e, f, g, h}, determinar o conjunto ∁A  B.
∁A = U – A = {f, g, h}
∁A  B = {f, g, h}  {d, e, f, g} = {f, g}
EXEMPLO:
33

34. Numa escola com 630 alunos, 250 estudam matemática, 210 estudam
física e 90 deles estudam as duas matérias.
Pergunta-se:
a) Quantos alunos estudam somente matemática?
b) Quantos alunos estudam somente física?
c) Quantos alunos estudam matemática ou física?
d) Quantos alunos não estudam nenhuma das duas matérias?
EXERCÍCIO:
34

35. DANTE, Luiz Roberto. Matemática Contexto & Aplicação. 2ª Edição. Volume 1. 1º
Ano do Ensino Médio. Editora Ática. São Paulo, 2014.
REFERÊNCIAS
35