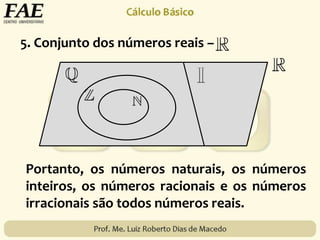
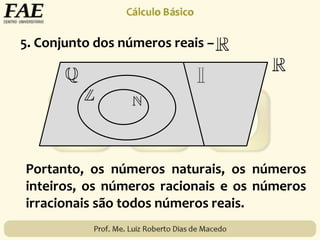
O documento descreve os principais conjuntos numéricos:
1) O conjunto dos números naturais, representado por {0, 1, 2, 3, ...}, que inclui subconjuntos como os números naturais não nulos.
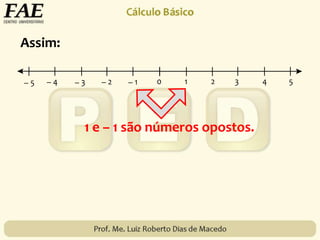
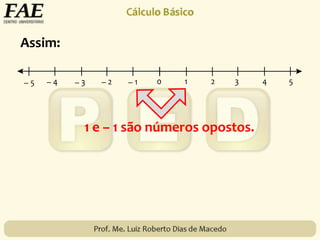
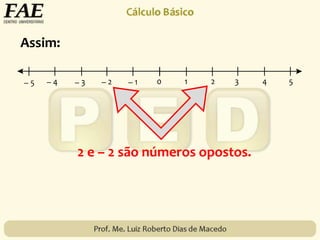
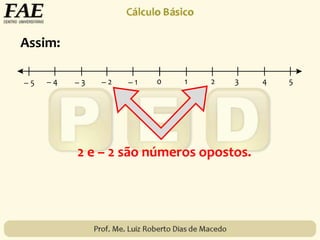
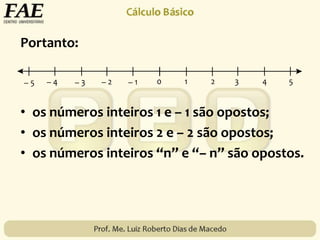
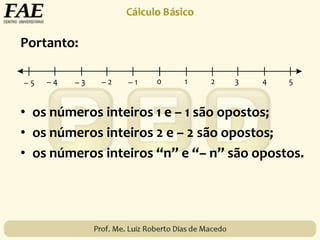
2) O conjunto dos números inteiros, representado por {..., -3, -2, -1, 0, 1, 2, 3, ...}, formado pelos números naturais e seus opostos.
3) Subconjuntos dos números inteiros como os números inteiros não nulos, não positivos e não negativos.