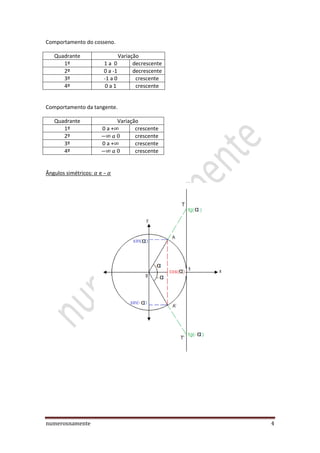
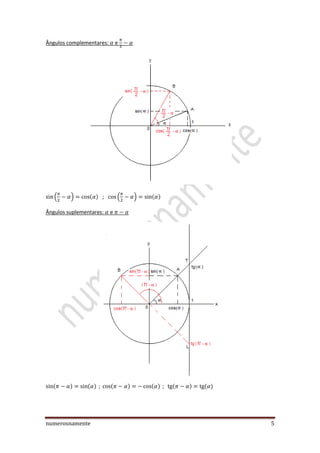
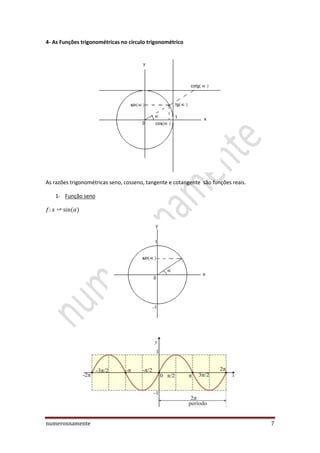
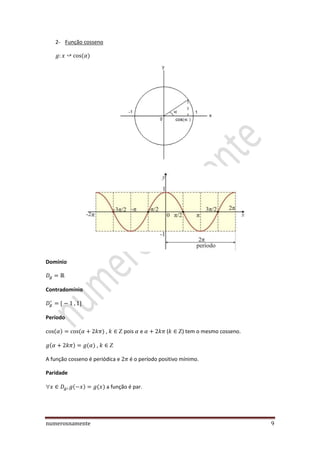
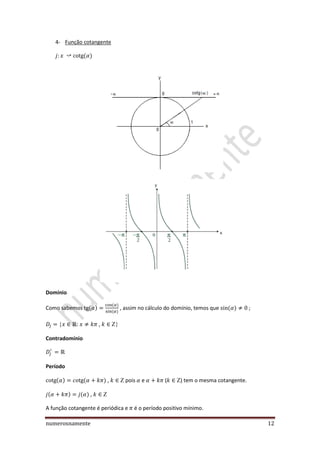
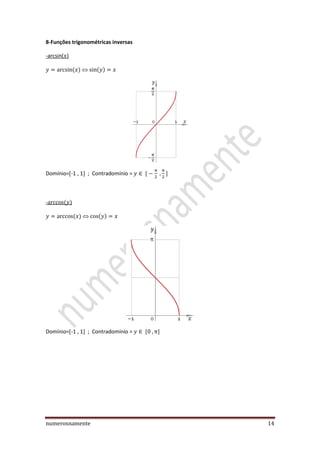
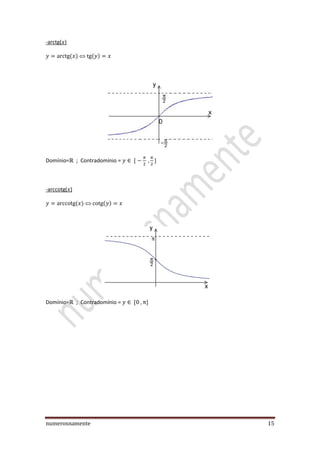
O documento discute a teoria básica da trigonometria, incluindo definições de funções trigonométricas, o círculo trigonométrico e suas propriedades. Também aborda tópicos como conversão entre graus e radianos, ângulos simétricos, complementares e suplementares, e as propriedades periódicas e de paridade das funções seno, cosseno, tangente e cotangente.

1. numerosnamente 1
Trigonometria
-Teoria-
1- Razões Trigonométricas de ângulos agudos
´=1
; ;
; ;
Cotangente =
Secante =
Cosecante = cosec (
Teorema de Pitágoras:
Fórmula fundamental da trigonometria:
se dividirmos tudo por obtem-se:
2- Ângulo e Arco generalizado
Para medir um ângulo, recorre-se geralmente a um transferidor. A medida do ângulo exprime-
se em graus.
O grau é assim a unidade de medida do sistema sexagesimal.
Um grau divide-se em subunidades: minuto e segundo

2. numerosnamente 2
;
No sistema circular, temos uma nova unidade de medida que é o radiano
Um radiano (rad) é a amplitude do ângulo ao centro que determina em qualquer
circunferência um arco de comprimento igual ao seu raio.
1 rad
Para converter graus em radianos e radianos em graus, temos:
e
3- Círculo Trigonométrico
O círculo trigonométrico é um círculo de centro na origem e raio igual a 1.
O círculo trigonométrico está dividido em 4 quadrantes.
Vamos agora determinar as várias razões trigonométricas:

3. numerosnamente 3
O ponto B é a projecção ortogonal de P sobre .
Assim ̅̅̅̅
O ponto C é a projecção ortogonal de P sobre
Assim ̅̅̅̅
̅̅̅̅
̅̅̅̅
̅̅̅̅
Os sinais das razões trigonométricas são:
1º quadrante 2º quadrante 3º quadrante 4º quadrante
seno + + - -
cosseno + - - +
tangente + - + -
cotangente + - + -
A variação das razões trigonométricas, em cada um dos quadrantes, consiste em analisar o
crescimento ou decrescimento destas à medida que as amplitudes dos ângulos aumentam.
Assim temos:
Comportamento do seno.
Quadrante Variação
1º 0 a 1 crescente
2º 1 a 0 decrescente
3º 0 a -1 decrescente
4º -1 a 0 crescente

4. numerosnamente 4
Comportamento do cosseno.
Quadrante Variação
1º 1 a 0 decrescente
2º 0 a -1 decrescente
3º -1 a 0 crescente
4º 0 a 1 crescente
Comportamento da tangente.
Quadrante Variação
1º 0 a + crescente
2º crescente
3º 0 a + crescente
4º crescente
Ângulos simétricos: e –

5. numerosnamente 5
Ângulos complementares: e
( ) ; ( )
Ângulos suplementares: e

6. numerosnamente 6
Ângulos que diferem de
; ;
Ângulos que diferem de :
( ) ; ( )

7. numerosnamente 7
4- As Funções trigonométricas no círculo trigonométrico
As razões trigonométricas seno, cosseno, tangente e cotangente são funções reais.
1- Função seno

8. numerosnamente 8
Domínio:
Contradomínio
Período
,  pois e ( ) tem o mesmo seno.
, 
A função seno é periódica e é o período positivo mínimo.
Paridade
 a função é impar.
Variação e Sinal
Se
Se
Se
Zeros, máximos e mínimos
Zeros: , 
Máximo = 1  ,
Mínimo=-1  ,

9. numerosnamente 9
2- Função cosseno
Domínio
Contradomínio
Período
,  pois e ( ) tem o mesmo cosseno.
, 
A função cosseno é periódica e é o período positivo mínimo.
Paridade
 a função é par.

10. numerosnamente 10
Variação e Sinal
Se
Se
Se
Zeros, máximos e mínimos
Zeros: , 
Máximo = 1  ,
Mínimo=-1  ,
3- Função tangente

11. numerosnamente 11
Domínio
Como sabemos , assim no cálculo do domínio, temos que ;
, 
Contradomínio
Período
,  pois e ( ) tem o mesma tangente.
, 
A função tangente é periódica e é o período positivo mínimo.
Paridade
 a função é impar.
Variação e Sinal
Se
Se
Se
Zeros, máximos e mínimos
Zeros: , 
Não tem máximos nem mínimos.

12. numerosnamente 12
4- Função cotangente
Domínio
Como sabemos , assim no cálculo do domínio, temos que ;
, 
Contradomínio
Período
,  pois e ( ) tem o mesma cotangente.
, 
A função cotangente é periódica e é o período positivo mínimo.

13. numerosnamente 13
Paridade
 a função é impar.
Variação e Sinal
Se
Se
Se
Zeros, máximos e mínimos
Zeros: , 
Não tem máximos nem mínimos.
5- Expressão geral das soluções da equação , sendo uma solução

, 
6- Expressão geral das soluções da equação sendo uma solução

, 
7- Expressão geral das soluções da equação sendo uma solução

, 

14. numerosnamente 14
8-Funções trigonométricas inversas
-arcsin( )

Domínio= -1 , 1 ; Contradomínio =
-

Domínio= -1 , 1 ; Contradomínio =

15. numerosnamente 15
-arctg( )

Domínio= ; Contradomínio =
-arccotg( )

Domínio= ; Contradomínio =