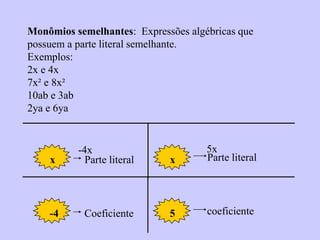
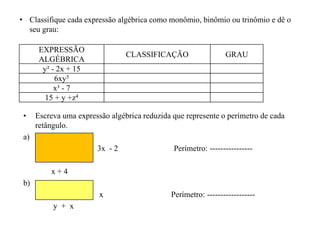
O documento resume os conceitos de monômios e polinômios. Monômios são expressões algébricas definidas pela multiplicação entre o coeficiente e a parte literal, enquanto polinômios são a soma de vários monômios. O documento explica como realizar operações como adição, subtração, multiplicação e divisão com monômios e polinômios, seguindo regras como somar ou subtrair apenas os coeficientes.

1. Monômios e
Polinômios

2. Monômios: Expressão algébrica definida apenas pela
multiplicação entre o coeficiente e a parte literal.
2x, 4ab, 10x²,
Sou Monômio
3x+5ya – 2y
Não sou Monômio

3. x Parte literal x Parte literal
Monômios semelhantes: Expressões algébricas que
possuem a parte literal semelhante.
Exemplos:
2x e 4x
7x² e 8x²
10ab e 3ab
2ya e 6ya
-4x 5x
-4 Coeficiente 5 coeficiente

4. Adição e Subtração de Monômios
2a + 7a = 9a
5x – 2x = 3x
10ab – 9ab = ab
6y – 9y = – 3y
7bc + 3cb = 10bc ou 10cb
– 12xy – 10xy = – 22xy
A adição e a subtração de
monômio devem ser
efetuadas quando as partes
literais são semelhantes.
Para efetuar as operações
entre monômios devemos
somar ou subtrair apenas
os coeficientes e
conservar a parte literal.

5. Multiplicação e Divisão entre Monômios
Ao multiplicar monômios em que as partes literais são
semelhantes devemos seguir os seguintes passos:
1º passo: multiplicar ou dividir os coeficientes
2º passo: conservar a parte literal e somar os expoentes.
Exemplos:
2x . 2x = 4x²
4xy . 6xy² = 24x²y³
10a²b . 9a²b³ = 90a4b4
5xyz . 6x²y³z = 30x³y4z²
5x³ : 5x² = x
10x²y² : 2x = 5xy²
30z : 5z = 6
20b³ : 10b = 2b²

6. Ao multiplicar monômios com parte literal
diferente devemos:
1º passo: multiplicar os coeficientes
2º passo: agrupá-las, se as letras forem diferentes
Exemplos:
2x . 3y = 6xy
4ab . 5z = 20abz
20c .2ab = 40abc
x . 6a = 6xa

7. No Processo de divisão de monômios é praticamente o
mesmo, exceto pelo fato de ao invés de somar os
expoentes devemos subtrair, depois fazemos a divisão
normalmente respeitando a relação de sinais e sempre
conservando a incógnita.
Exemplos:
x³: x = x²
y²: y = y
25ab: 5b = 5a
8 x³:2 x² = 4x

8. Potência de Monômios
São várias as
propriedades que
formam as regras de
potenciação de
números reais.
Potência de potência
Iremos aplicar essa
propriedade no
cálculo de potência de
monômios.
• Exemplos

9. EXERCÍCIOS
1. Efetue.
a) ( + 7x) + ( - 3x )=
b) ( - 8x) + (+ 11x)=
c) ( - 2y) + ( - 3y )=
d) (- 2m) + ( - m )=
e) ( -72 x) + (+ 14 x)=
f) ( + 8x) - ( - 3x)=
g) ( - 6y) - ( - y )=
h) ( - 5x) – ( - 11x)=
i) ( + 7y) - ( + 7y)=
2. Multiplique os monômios.
a) (+5x) . (- 4x2)=
b) (-2x) . (+ 3x)=
c) ( - a) . (+ 6a)=
d) (+4x2) . (+5x3)=
e) (+2a) . (- 7b)=
f) ( - 2x) . ( - 3y)=
g) (3x) . (5y )=
h) (3ab) . (2a)=

10. 4. Complete a tabela
3. Escreva se os termos algébricos em
cada item são ou não semelhantes.
a) 4x2 e 4x3
b) x e -x
c) 5xy2 e 7xy2
d) 7ab e 6ba
e) 9x e 9y
f) 9y e -2y
g) 4xy3 e 4x3y
h) xy e -xy
Monômio
Coeficiente
numérico
Parte literal
2a
-8 b
15
2xy
1 ab²
15a³b
-7 a

11. 5. Reduza os termos semelhantes:

12. Polinômios: Soma de vários monômios
• Exemplos:
• 3x²- 6x + 4
• 2x² + 4x – 7
• x²-6x+4+x
• x²+2x²-6
• 5x²-2x-3

13. Adição e Subtração de Polinômios
Subtraindo –3x² + 10x – 6 de 5x² – 9x – 8.
(5x² – 9x – 8) – (–3x² + 10x – 6) → eliminar
os parênteses utilizando o jogo de sinal.
– (–3x²) = +3x²
– (+10x) = –10x
– (–6) = +6
5x² – 9x – 8 + 3x² –10x +6 → reduzir os
termos semelhantes.
5x² + 3x² – 9x –10x – 8 + 6
8x² – 19x – 2
Portanto: (5x² – 9x – 8) – (–3x² + 10x – 6) =
8x² – 19x – 2
Adicionar x² – 3x – 1 com –3 x² + 8x – 6.
(x² – 3x – 1) + (–3x² + 8x – 6) → eliminar
o segundo parênteses através do jogo de
sinal.
+(–3x²) = –3x²
+(+8x) = +8x
+(–6) = –6
x² – 3x – 1 – 3x² + 8x – 6 → reduzir os
termos semelhantes.
x² – 3x² – 3x + 8x – 1 – 6
–2x² + 5x – 7
Portanto: –2x² + 5x – 7

14. Exercícios
1) Efetue as seguintes adições:
a) (2x²-9x+2) + (3x²+7x-1)
b) (5x²+5x-8) + (-2x²+3x-2)
c) (3x-6y+4) + (4x+2y-2)
d) (5x²-7x+2) + (2x²+7x-1)
e) (4x+3y+1) + (6x-2y-9)
f) (2x³+5x²+4x) + (2x³-3x²+x)
g) (5x²-2ax+a²) + (-3x²+2ax-a²)
h) (y²+3y-5) + (-3y+7-5y²)
i) (x²-5x+3) + (-4x²-2x)
j) (9x²-4x-3) + (3x²-10)
2) Efetue as seguintes subtrações:
a) (5x²-4x+7) - (3x²+7x-1)
b) (6x²-6x+9) - (3x²+8x-2)
c) (7x-4y+2) - (2x-2y+5)
d) (4x-y-1) - (9x+y+3)
e) (-2a²-3ª+6) - (-4a²-5ª+6)
f) (4x³-6x²+3x) - (7x³-6x²+8x)
g) (x²-5x+3) - (4x²+6)
h) (x²+2xy+y²) - (y²+x²+2xy)
i) (7ab+4c-3a) - (5c+4a-10)

15. Respostas
Ex. 1
a) (5x² -2x + 1)
b) (3x² + 8x - 10)
c) (7x -4y +2)
d) (7x²+ 1)
e) (10x +1y-8)
f) (4x³ +2x²+ 5x)
g) ( 2x²)
h) ( -4y² + 2)
i) (-3x² - 7x + 3)
j) (12x² -4x- 13)
Ex. 2
a) 2x² - 11x + 8
b) 3x² - 14x + 11
c) 5x - 2y – 3
d) -5x – 2y – 4
e) -2a² +2a
f) -3x³ - 5x
g) -3x² -5x -3
h) 0
i ) 7ab -c-7a + 10

16. MULTIPLICAÇÃO DE MONÔMIO POR POLINÔMIO
2x . (7x2 – 4x + 5) = 2x . (7x2) - 2x . (-4x) + 2x . (5) = 14x3 + 8x2 + 10x
O exemplo nos mostra que:
Multiplicamos o monômio por todos os termos do
polinômio.
.

17. MULTIPLICAÇÃO DE POLINÔMIO POR
POLINÔMIO
• ( x + 4 ) . ( x – 2 ) = x2 – 2x + 4x – 8 = x2 + 2x – 8
Na prática:
• Multiplicamos cada termo do primeiro polinômio por todos
os termos do segundo polinômio e, a seguir, reduzimos os
termos semelhantes.

18. • Calcule os produtos
a) 3 (x+y) ____ (R: 3x +3y)
b) 7 (x-2y) ___ (R: 7x - 14y)
c) 2x (x+y) ___ (R: 2x² + 2xy)
d) 4x (a+b) ___ (R: 4xa + 4xb)
e) 2x(x²-2x+5) _ (R:2x³ - 4x² + 10x)
f) (x+5).(x+2) __ (R: x² +7x +10)
g) (3x+2).(2x+1) __ (R: 6x² +7x + 2)
h) (x+7).(x-4) ____ (R: x² +3x -28)
i) (3x+4).(2x-1) ___ (R: 6x² +5x -4)
j) (x-4y).(x-y) ____ (R: x² -5xy + 4y²)
k) (5x-2).(2x-1) ___ (R: 10x² -9x + 2)
l) (3x+1).(3x-1) ___ (R: 9x² - 1)
m) (2x+5).(2x-5) __ (R: 4x² - 25)

19. EXPRESSÃO
ALGÉBRICA
CLASSIFICAÇÃO GRAU
y² - 2x + 15
6xy5
x³ - 7
15 + y +z4
• Escreva uma expressão algébrica reduzida que represente o perímetro de cada
retângulo.
a)
3x - 2 Perímetro: ----------------
x + 4
b)
x Perímetro: ------------------
y + x
• Classifique cada expressão algébrica como monômio, binômio ou trinômio e dê o
seu grau: