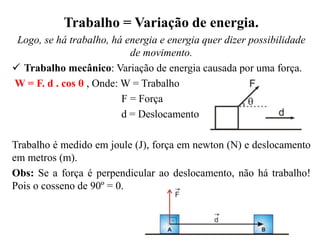
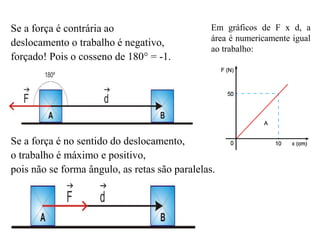
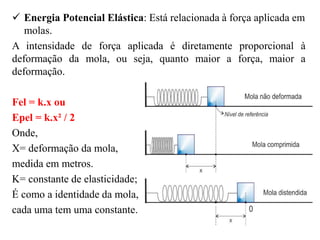
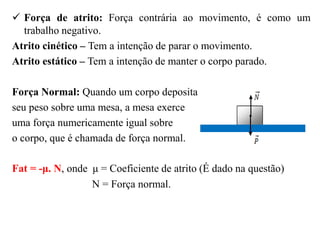
O documento aborda os conceitos de trabalho e energia, definindo trabalho mecânico como a variação de energia resultante da aplicação de uma força. Também aborda a energia cinética e potencial, além das forças de atrito e normal, e fornece exemplos de exercícios práticos relacionados ao cálculo do trabalho e energia. Notações e fórmulas essenciais são apresentadas para facilitar a compreensão dos conceitos físicos.

1. Trabalho e energia
Resumo e Exercícios

2. Trabalho = Variação de energia.
Logo, se há trabalho, há energia e energia quer dizer possibilidade
de movimento.
 Trabalho mecânico: Variação de energia causada por uma força.
W = F. d . cos θ , Onde: W = Trabalho
F = Força
d = Deslocamento
Trabalho é medido em joule (J), força em newton (N) e deslocamento
em metros (m).
Obs: Se a força é perpendicular ao deslocamento, não há trabalho!
Pois o cosseno de 90º = 0.

3. Se a força é contrária ao
deslocamento o trabalho é negativo,
forçado! Pois o cosseno de 180° = -1.
Se a força é no sentido do deslocamento,
o trabalho é máximo e positivo,
pois não se forma ângulo, as retas são paralelas.
Em gráficos de F x d, a
área é numericamente igual
ao trabalho:

4. Equações importantes!
Força peso: P = m.g
Força: F = m.a
Aceleração: a = v/t
Velocidade: v= s/t
Gravidade (g) = 10m/s²
Onde,
m = Massa; Medida em KG
t = tempo; Medido em Segundos (s)
V = Velocidade; Medida em m/s.
a = aceleração; Medida em m/s².

5.  Energia Cinética: Está associada ao movimento do corpo.
Quando uma força realiza trabalho sobre um corpo, ela transfere
energia a ele, que pode se manifestar em forma de movimento.
Ec = m.v² / 2
 Energia Potencial gravitacional: Está relacionada à posição
do corpo em relação à gravidade.
Epg = m.g.h, onde h = altura; medida em metros.
A energia potencial gravitacional funciona juntamente com a
cinética, pois quando o corpo ganha altura, ele armazena energia,
que pode ser transformada em movimento, por exemplo, nessa
rampa.
h
30º
Epg Ec
a = g. sen θ
V² = Vo² + 2.a.h

6.  Energia Potencial Elástica: Está relacionada à força aplicada em
molas.
A intensidade de força aplicada é diretamente proporcional à
deformação da mola, ou seja, quanto maior a força, maior a
deformação.
Fel = k.x ou
Epel = k.x² / 2
Onde,
X= deformação da mola,
medida em metros.
K= constante de elasticidade;
É como a identidade da mola,
cada uma tem uma constante.

7.  Força de atrito: Força contrária ao movimento, é como um
trabalho negativo.
Atrito cinético – Tem a intenção de parar o movimento.
Atrito estático – Tem a intenção de manter o corpo parado.
Força Normal: Quando um corpo deposita
seu peso sobre uma mesa, a mesa exerce
uma força numericamente igual sobre
o corpo, que é chamada de força normal.
Fat = -μ. N, onde μ = Coeficiente de atrito (É dado na questão)
N = Força normal.

8. Exercícios
1. Imagine a seguinte situação: um operário da
construção civil precisa carregar um saco de cimento
de 50 kg. Ele levanta esse saco de cimento e se
desloca por 20 metros na horizontal. Adote g = 10
m/s². Calcule o trabalho realizado pela força do
operário sobre o cimento.
a) 1000 J
b) 2500 J
c) 0 J
d) 10000J
e) 50 J

9. Resposta:
A resposta é zero. Embora o operário exerça uma
força em módulo igual ao peso do saco de cimento,
que é de 500 N, essa força é na vertical, enquanto
seu deslocamento é na horizontal, ou seja, o ângulo
entre a força e o deslocamento é 90°. Quando a
força e o deslocamento formam um ângulo igual a
90°, o trabalho realizado por essa força é nulo. Veja:
T = F . d . cos θ
θ = 90°, logo cos 90° = 0, então T = 0.
Alternativa "c".

10. 2. Um objeto de massa 5 kg é deixado cair de
uma determinada altura. Ele chega ao solo com
energia cinética igual 2000 J. Determine a altura
que o objeto foi abandonado. Despreze o atrito
com o ar e considere g = 10 m/s².
a) 100m
b) 50m
c) 75m
d) 40m
e) 25m

11. No início só temos energia potencial
gravitacional, pois o objeto é abandonado de
certa altura. Ao ser abandonado, toda energia
potencial gravitacional se converteu em energia
cinética. Então:
m .g. h = 2000, logo 5 . 10 . h = 2000
h = 2000/50
h = 40 m

12. 3. Qual é a variação da energia cinética de um
objeto de massa m que se encontra sobre um plano
horizontal quando sobre ele for aplicada uma força
de intensidade 50 N que forma um ângulo de 60°
com a horizontal e arrasta-o por 5m?
a) 155 J
b) 220 J
c) 350 J
d) 125 J
e) 555 J

13. A partir da definição de que o trabalho é a
variação da energia cinética, podemos escrever:
T = ΔEc (Δ= Variação)
ΔEc = F. d. cos60º
ΔEc = 50. 5. 0,5
ΔEc = 125 J