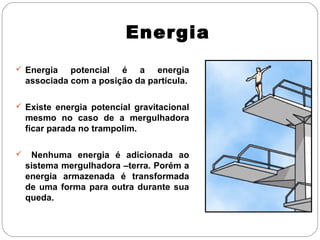
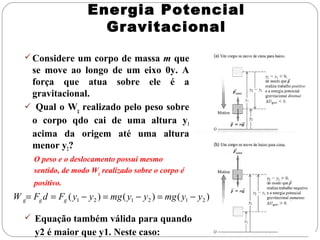
[1] O documento discute os conceitos de energia potencial gravitacional, energia cinética, trabalho realizado por forças e a conservação da energia mecânica. [2] A energia potencial gravitacional depende da posição de um corpo em relação a uma referência e pode ser convertida em energia cinética. [3] Quando uma força conservativa realiza trabalho sobre um sistema, a variação na energia cinética é igual à variação na energia potencial do sistema, de modo que a energia mecânica total se mantém constante

1. Energia e trabalho
Profª Michelle Paiva

2. Energia
 Energia potencial é a energia
associada com a posição da partícula.
 Existe energia potencial gravitacional
mesmo no caso de a mergulhadora
ficar parada no trampolim.
 Nenhuma energia é adicionada ao
sistema mergulhadora –terra. Porém a
energia armazenada é transformada
de uma forma para outra durante sua
queda.

3. Energia Cinética
ENERGIA CINÉTICA (K)
 A energia cinética é a energia associada ao estado de
movimento de um
objeto.
 Quanto mais rapidamente um objeto estiver se movendo,
maior será sua energia cinética. Quando o objeto está em repouso, sua
energia cinética é nula.

4.  Para um objeto de massa m cuja velocidade v é bem inferior à
velocidade da luz, definimos a sua energia cinética como
K = ½ mv2
 A unidade de SI para a energia cinética (e todos os outros
tipos de energia) é o joule ( J ), em homenagem a James
Prescott Joule, um cientista inglês do século XIX.

5. TRABALHO
Na linguagem comum, a palavra
trabalho é aplicada a qualquer forma de
atividade que requeira um esforço
muscular ou mental. Em física,
entretanto, este termo é usado num
sentido mais específico, que envolve a
aplicação de uma força a um corpo e o
deslocamento deste corpo.

6. TRABALHO DE UMA FORÇA CONSTANTE SOBRE
UM OBJETO QUE SE MOVE EM UMA DIMENSÃO
r
F
θ
r
d
r r
W = F .d ⇒ W = Fd cos θ

7.  O trabalho é uma grandeza algébrica, que
pode ser positivo ou negativo. Quando a força
possui uma componente na mesma direção e
sentido que o deslocamento, o trabalho
realizado por ela é positivo.
 Se o sentido da componente da força for
oposto ao deslocamento, o trabalho será
negativo. Se a força for perpendicular ao
deslocamento, ela não terá componente na
direção do deslocamento e o trabalho será
nulo.

8. TEOREMA DO TRABALHO-ENERGIA
CINÉTICA
 O trabalho realizado pela força resultante
sobre uma partícula é igual à variação da
energia cinética da partícula
1 2 1 2
W = ∆ K ⇒ W = mv − mv0
2 2

9. Se o trabalho resultante realizado sobre
uma partícula for positivo, então a
energia cinética da partícula aumenta
de uma quantidade igual ao trabalho.
Se o trabalho resultante for negativo,
então a energia cinética da partícula
diminui de uma quantidade igual ao
trabalho.

10. TRABALHO REALIZADO POR UMA FORÇA
VARIÁVEL: EM UMA DIMENSÃO
Para uma força constante e de mesma
direção e sentido do deslocamento é fácil
verificar que o trabalho realizado por ela é
igual a “área sob a curva” no gráfico , como
está representado na figura abaixo. Mesmo
quando o valor da força estiver variando esta
propriedade é válida, sendo que o trabalho de
uma força variável na direção x pode ser
calculada por

11. x2
w = ∫ F ( x ) dx
x1
w
x1 x2

12. TRABALHO REALIZADO POR UMA
FORÇA DE MOLA
A força exercida pela mola pode,
portanto, ser expressa em termos de
distância x, através da qual ela é
esticada ou comprimida, a partir do seu
comprimento de equilíbrio, por
F = − kx

13. xF xF xF
W= ∫ F ( x) dx = ∫ −kx dx = −k ∫ xdx
xi xi xi
1 2 2 1 2 2
= − k ( x f − xi ) = k ( xi − x f )
2 2

14. POTÊNCIA
A potência devido a uma força é a taxa
com que essa força realiza um trabalho
sobre um objeto. Se a força realiza um
trabalho W durante um intervalo de
tempo é Δt, a potência média é
W
Pm =
∆t

15. A potência instantânea P é a taxa
instantânea de realização de trabalho,
que pode ser escrita como
dW
P=
dt

16. Energia
 Como a transformação pode ser
entendida a partir do teorema
trabalho energia.
 Veremos que a soma da energia
cinética e potencial fornece a
energia mecânica total do sistema e
essa energia permanece constante
durante o movimento do sistema
(lei da conservação da energia)

17. Energia Potencial
Gravitacional
 Em muitas situações tudo se passa
como se “a energia fosse
armazenada em um sistema para
ser recuperado depois.”
 Garoto em um balanço: Nos pontos
mais elevados, a energia é  Esse ex. da idéia de que
armazenada em outra forma, existe uma energia
relacionada com a altura do ponto associada com a posição
acima do solo, e esta energia é dos corpos em um sistema.
Este tipo de energia
convertida em K quanto atinge o fornece o potencial ou a
ponto inferior do arco. possibilidade de realizar
trabalho (W)

18. Energia Potencial
Gravitacional
 Quando um martelo é elevado no ar,
existe um potencial para um trabalho
sobre ele ser realizado pela força da
gravidade, porém isso só ocorre
quando o martelo é liberado. Por esse
motivo, a energia associada com a
posição denomina-se ENERGIA
POTENCIAL.
 Existe uma energia potencial
associada com o peso do corpo e com
a altura acima do solo. Chamamos
essa energia de ENERGIA
POTENCIAL GRAVITACIONAL.

19. Energia Potencial
Gravitacional
 Quando um corpo cai sem resistência
do ar, a energia potencial diminui à
medida que a energia cinética
aumenta.
 Vimos “ usando o teorema do
trabalho-energia para concluir que K
do corpo em queda livre aumenta
porque a força gravitacional realiza
trabalho sobre ele.
 Usaremos o teorema W-∆K para demonstrar que essas duas
descrições de um corpo são equivalentes e para deduzir uma
expressão para energia potencial.

20. Energia Potencial
Gravitacional
 Considere um corpo de massa m que
se move ao longo de um eixo 0y. A
força que atua sobre ele é a
gravitacional.
 Qual o Wg realizado pelo peso sobre
o corpo qdo cai de uma altura y1
acima da origem até uma altura
menor y2?
O peso e o deslocamento possui mesmo
sentido, de modo Wg realizado sobre o corpo é
positivo.
W g= Fg d = Fg ( y1 − y2 ) = mg ( y1 − y2 ) = mg ( y1 − y2 )
 Equação também válida para quando
y2 é maior que y1. Neste caso:

21. Energia Potencial
Gravitacional
 Podemos expressar Wg em termos da quantidade mgy no início
e no final do deslocamento.
U = mgy Energia potencial
gravitacional
 Seu valor inicial é U1 = mgy1 e seu valor final U2 = mgy2;
∆U = U 2 − U1
 Podemos expressar Wg realizado pela força gravitacional
durante o deslocamento de y1 a y2 como
W = U1 − U 2 = −(U 2 − U1 ) = −∆U
 Corpo se move de baixo para cima - y aumenta; Wg (-);
U aumenta (∆U >0).
 Corpo se move de cima para baixo - y diminui; Wg (+);
U diminui (∆U >0).

22. Forças conservativas e não
conservativas
 As forças que atuam num sistema,
modificando-lhe a configuração,
dizem-se conservativas quando,
regressando o sistema à configuração
inicial, readquire também a energia
cinética inicial.
 Isto significa que as forças
conservativas conservaram a
capacidade que o sistema tinha de
realizar trabalho, e daí o seu nome.
 Fg realiza de A a B, um trabalho resistente, que se traduz num aumento de energia
potencial do sistema. Segue-se, depois, um trabalho potente, de B para A, que se traduz
na restituição à forma cinética do incremento de energia potencial que tinha sido
armazenada.

23. Forças conservativas e não
conservativas
 As forças que atuam num sistema dizem-
se não conservativas ou dissipativas
quando, ao deixarem de realizar trabalho,
o sistema ou não regressa à configuração
inicial ou regressa a ela com energia
cinética diferente da que tinha no
princípio.
 Isto quer dizer que as forças não conservativas não conservaram
a capacidade que o sistema tinha de realizar trabalho.
 A força de atrito, realiza sempre trabalho resistente não traduzido em aumento de
energia potencial

24. Independência da trajetória para
o trabalho de forças
conservativas
 Consideremos uma partícula em movimento em um percurso
fechado, se o W realizado pela força neste percurso for nulo,
então dizemos que as forças são conservativas.
 Ou seja, a energia total que se transfere da partícula e para a
partícula durante a viaje de ida e volta ao longo do percurso fechado
é nula.
Exemplo: O lançamento de um tomate.
Wres = 0
“O WR realizado pela força conservativa
movendo-se entre dois pontos não depende
da trajetória.”

25. Independência da trajetória para
o trabalho de forças
conservativas
 Consideremos um percurso fechado
arbitrário para uma partícula sujeita a uma
ação de uma única força.
 A partícula se move do ponto inicial a
para um ponto final b ao longo da trajetória
1 e retorna pela trajetória 2.
“A força realiza W sobre a partícula a medida que ela se movimenta ao
longo de cada trajetória.”
• O W realizado de a até b ao longo da trajetória 1 é: Wab,1
• O W realizado da volta de b até a é; Wba,2

26.  Se F for conservativa; Wres = 0.
Wab ,1 + Wba , 2 = 0
Wab ,1 = −Wba , 2
 O W realizado ao longo da trajetória de ida é igual ao negativo
do W realizado ao longo da volta.
 Consideremos o Wab,2 realizado pela força sobre a partícula
quando ela se move de a até b ao longo da trajetória 2.
Wab , 2 = −Wba , 2
Substituindo a equação acima na equação anterior.
Wab ,1 = −Wab , 2
Portanto o W independe da trajetória quando F for conservativa.

27. Determinando Valores de
Energia Potencial
 Encontrar a energia potencial dos dois tipos de energia
discutido nesta seção: energia potencial gravitacional e energia
potencial elástica.
 Encontrar uma relação geral entre uma força conservativa e a
energia potencial a ela associada.
• Considere um objeto que se comporta como uma partícula e que
é parte de um sistema no qual atua uma F conservativa.
“ quando esta força realiza W sobre o objeto, a variação ∆U na energia
potencial associada ao sistema é o negativo do W.”
W = −∆U

28. Determinando Valores de
Energia Potencial
 No caso geral onde a força pode variar com a posição
xf
W = ∫ F ( x)dx
xi
Substituindo W = - ∆U, temos:
xf
∆U = − ∫ F ( x)dx
xi
Relação geral entre força e energia potencial.

29. Energia Potencial
Gravitacional
 Consideremos uma partícula com massa m movendo-se
verticalmente ao longo de y (positivo para cima). A medida que
a partícula se move do ponto y1 para y2 a Fg realiza W sobre ela.
xf xf
∆U = − ∫ F ( x)dy = − ∫ (−mg )dy = mg | y12 = mg∆y
y
xi xi
Podemos usar configurações de referência na qual a partícula esta
em um ponto de referência yi que tomamos como U = 0. Portanto:
U ( y ) = mgy
“a energia potencial gravitacional associada ao sistema partícula-terra depende apenas
da
Posição vertical y da partícula em relação à posição de referência y = 0, e não da

30. Energia Potencial Elástica
 Consideremos um sistema massa-mola, com o bloco se
movendo na extremidade de uma mola de constante elástica k.
Enquanto o bloco se move do ponto xi para o xf, a força da mola
F = -kx realiza W sobre o bloco.
xf xf
1
∆U = − ∫ F ( x)dx = − ∫ (−kx)dx = kx | x12 =
x k∆x
xi xi
2
1 2 1 2
∆U = kx f − kxi
2 2
Escolhendo um valor de referência U com o bloco na posição x na
qual a mola se encontra relaxado x= 0.
1 2 1
U −0 = kx − 0; U = kx 2
2 2

31. Conservação da Energia
Mecânica
 A energia mecânica de um sistema é a soma da energia cinética
e potencial dos objetos que compõem o sistema:
Emec = K + U
Energia mecânica: Forças conservativas e o sistema é isolado (F ext
= 0).
 Quando uma F conservativa realiza W sobre um objeto dentro
de um sistema, essa força transfere energia entre a K do objeto e
a U do sistema. Pelo teorema W-∆K
∆K = W

32. Conservação da Energia
Mecânica
 Usando a equação da variação na energia potencial
∆U = −W
Combinando as duas equações anteriores
∆K = −∆U
Uma dessas energias aumenta na mesma quantidade que a outra
diminui.
Podemos reescrever como
K 2 − K1 = −(U 2 − U1 ) Conservação da energia
K 2 + U 2 = K1 + U1 mecânica.

33. Conservação da Energia
Mecânica
“Em um sistema isolado onde apenas forças conservativas causam
variações de energia, a energia cinética e a energia potencial podem
variar, mas a sua soma, a energia mecânica Emec do sistema, não pode
variar”
Este resultado é chamado de PRINCÍPIO DE
CONSERVAÇÃODA
ENEGIA MECÂNICA.
Este princípio nos permite resolver
Podemos escrever esse princípio de outra forma
∆Emec = ∆K + ∆U Problemas que seriam difíceis usando
apenas as Leis de Newton.
Quando a energia se conserva, podemos a soma de K e U em cada instante com aquele novo instante
sem considerar o movimento intermediário e sem determinar o WR das F envolvidas.

34. Conservação da Energia
Mecânica
 Exemplo do princípio de conservação aplicado: Enquanto um
pêndulo oscila, a energia do sistema pêndulo-terra é transferida
entre K e U, com a soma K+U permanecendo constante.
 Se conhecermos a Ug quando a massa do pêndulo esta no seu ponto
mais alto, a equação da conservação da energia nos fornece a K do
ponto mais baixo.
 Vamos escolher o ponto mais baixo como ponto de referência,
com U2 = 0 e no ponto mais alto U1 = 20 J. Como a massa pará
momentaneamente no ponto mais alto, K1 = 0. Qual a energia no
ponto mais baixo?
K 2 + 0 = 0 + 20; K 2 = 20 J

36. Interpretando uma curva de
energia potencial
 Consideremos uma partícula que faz parte de um sistema no
qual atuam uma força conservativa. O movimento da partícula
se dar ao longo de um eixo x enquanto a F conservativa realiza
W sobre ela.
 Podemos obter bastante informação sobre o movimento da
partícula a partir do gráfico energia potencial do sistema U(x).
 Vimos que se conhecemos a F(x) que atua sobre a partícula
podemos encontrar a energia potencial
xf
∆U = − ∫ F ( x)dx
xi

37. Interpretando uma curva de
energia potencial
 Queremos fazer agora o contrário; isto é, conhecemos a energia
potencial U(x) e queremos determinar a força.
 Para o movimento em uma dimensão, o W realizado pela força
que atua sobre a partícula se move através de uma distância ∆x é
F(x) ∆x. Podemos escrever
∆U = −W = − F ( x)∆x
Passando ao limite diferencial
dU ( x)
F ( x) = −
dx

38. Interpretando uma curva de
energia potencial
 Verificar este resultado U(x) = ½ kx2 que é a energia potencial
elástica e U(x) = mgx.
 A curva de energia potencial
- U versus x : podemos encontrar F
medindo a inclinação da
curva de U(x) em vários
pontos.

39. Interpretando uma curva de
energia potencial
 Pontos de retorno
Na ausência da força conservativas, a energia mecânica E de um
Sistema possui um valor constante dado por
K ( x) + U ( x) = Emec
K(x) é uma função energia cinética de uma partícula no sistema.
K ( x) = Emec − U ( x)
Como Emec é constante, pelo ex. anterior igual a 5 J. Portanto no
ponto x5
K ( x) = 5 − 4 = 1J

40. Interpretando uma curva de
energia potencial
 Pontos de Retorno
 O valor de K máximo (5J) é no ponto x2 quando U(x) é mínimo.
• K nunca pode ser negativo (v2), a partícula não pode se mover a
para esquerda de x1, Emec – U(x) é negativo. Quando a partícula se
move em direção a x1 a partir de x2, K diminui até K = 0 em x1.
• Em x1 – a força é positiva (inclinação negativa). Significa que a
partícula não permanece em x1, mas começa a se mover para
direita, em sentido oposto ao seu movimento anterior. Portanto
x1 é um PONTO DE RETORNO, um lugar onde K = 0 (pois U
= E) e a partícula inverte o sentido do movimento.

41. Interpretando uma curva de
energia potencial
Pontos de Equilíbrio
 3 valores diferentes de Emec.
 Se Emec = 4 J, o ponto de retorno
mudar de x1 para um valor entre x1
e x2 .
 Qualquer ponto a direita de x5, a
energia mecânica do sistema é
igual a U(x); portanto, K = 0
e nenhuma força atua sobre a mesma, de modo que ela precisa está
em repouso. Diz-se que a partícula em tal posição está em
EQUILÍBRIO NEUTRO.

42. Interpretando uma curva de
energia potencial
Pontos de Equilíbrio
 Se Emec = 3 J, existe dois pontos de
retorno: um entre x1 e x2 e outro
entre x4 e x5. Além disso x3 é um
ponto onde K = 0. Se a partícula
estiver neste ponto, a F = 0 e a
partícula permanecerá em
repouso.
Se ela for ligeiramente deslocada em qualquer um dos dois sentidos,
uma força não nula a empurra no mesmo sentido e a partícula
continua se afastando ainda mais do ponto inicial. Uma partícula em
tal posição é considerada em EQUILÍBRIO INSTÁVEL.

43. Interpretando uma curva de
energia potencial
Pontos de Equilíbrio
 Se Emec = 1 J. Se colocarmos em x4
ela permanecerá nesta posição.
Ela não pode se mover nem para
direita nem para esquerda por sua
conta própria, pois seria
necessário uma K negativa.
Se empurramos ligeiramente para a esquerda ou para direita, aparece
uma força restauradora que a faz retornar ao ponto x4. Uma partícula
em tal posição é considerada em EQUILÍBRIO ESTÁVEL.

44. Trabalho Realizado por uma
Força Externa sobre um Sistema
vimos: “ O W é a energia transferida PARA um sistema ou
DE
um sistema devido a atuação de uma força externa sobre este
sistema.”
Podemos extender esse conceito para uma Fext atuando sobre
Um sistema.
Quando a transferência de Quando a transferência de
energia é PARA o sistema. energia é DO o sistema.

45. Trabalho Realizado por uma
Força Externa sobre um Sistema
NA AUSÊNCIA DE ATRITO
Num boliche quando você vai arremessar a bola, inicialmente você
se agacha e coloca suas mãos em forma de concha por debaixo da
bola sobre o peso.
Depois você levanta rapidamente enquanto ao mesmo tempo puxa
suas mãos bruscamente, lançando a bola para cima no nível do rosto.
Durante o seu movimento para cima, a F que vc aplica realiza W, isto
é, ela é uma força externa que transfere energia, mas para qual
sistema?

46. Trabalho Realizado por uma
Força Externa sobre um Sistema
NA AUSÊNCIA DE ATRITO
Verificar quais energias se modificam:
Há variação ∆K da bola, e como a bola e a terra ficaram afastada,
também houve uma variação ∆Ug do sistema bola-terra.
Para incluir essas variações, precisamos considerar o sistema bola-
terra. Assim F é uma Fext que realiza W sobre o sistema, e o W é
W = ∆K + ∆U = ∆Emec
Energia equivalente para o W realizado por Fext
sobre um sistema sem atrito.

47. NA PRESENÇA DE ATRITO
Consideremos um sistema onde uma F horizontal constante puxa o bloco
ao longo do eixo x deslocando-o por uma distância d e aumentando a velo-
cidade do bloco de v0 para v.
O bloco será nosso sistema. Aplicando a segunda lei de Newton
F − f c = ma

48. Como as forças são constantes v 2 = v0 + 2ad , temos
2
Fd = ∆K + f c d
Numa situação mais geral (uma na qual o bloco esteja subindo uma
rampa), pode haver uma variação na energia potencial. Para incluir
tal variação, temos
Fd = ∆Emec + f c d
Verificamos experimentalmente que o bloco e a porção do piso ao
longo do qual ele se desloca ficam aquecidos enquanto o bloco
desliza. Portanto foi verificado experimentalmente que essa energia
térmica é igual
∆ET = f c d
Portanto
Trabalho realizado pelo sistema
W = ∆Emec + ET em presença de atrito.

49. Conservação da Energia
Todos os casos discutidos até agora obedecem a LEI DE
CONSERVAÇÃO,
que está relacionada com a energia total de um sistema. Essa energia total é
a soma da energia mecânica com a térmica ou qualquer outro tipo de
energia interna.
“A energia total E de um sistema pode mudar apenas por quantidades de
energias que são transferidas para o sistema ou delas retiradas.”
O único tipo de energia de transferência de energia que consideramos e o W
realizado sobre um sistema. Assim, esta lei estabelece
W = ∆E = ∆Emec + ∆ET + ∆Eint
A lei de conservação de energia é algo baseado em inúmeros experimentos.

50. Conservação da Energia
SISTEMA ISOLADO
Se um sistema está isolado de uma vizinhança, não podendo haver
trocas com a vizinhança. Para este caso a lei de conservação da
energia diz:
“A energia total E, de um sistema isolado não pode variar.”
Pode haver muitas transferências dentro do sistema; energia cinética
em energia potencial ou térmica, entretanto a energia total do sistema
não pode variar.

51. Conservação da Energia
A conservação da energia pode der escrita de duas maneiras:
∆Emec + ∆ET + ∆Eint = 0 W =0
e
Emec , 2 = Emec ,1 − ∆ET − ∆Eint
“Em um sistema isolado, podemos relacionar a energia total em um
dado instante com a energia total em outro instante sem ter que
considerar as energias em tempos intermediários.”

52. FORÇAS EXTERNAS E TRANSFERÊNCIA DE ENERGIA INTERNA
Uma força externa pode mudar a K ou U de um
objeto sem realizar W, isto é, sem transferir energia
para o objeto. Em vez disso, é a força responsável
pela transferência de energia de uma forma para
outra dentro do objeto.
Patinadora no gelo, inicialmente em repouso, empurra
um corrimão e passa a deslizar sobre o gelo. Sua K
aumenta porque o corrimão exerceu uma Fext sobre ela.
No entanto a F não transfere energia para o corrimão
para ela. Assim a força não realiza W sobre ela. Ao
contrário a K aumenta como resultado de transferências
internas a partir da energia bioquimica contida nos seus
musculos.

53. FORÇAS EXTERNAS E TRANSFERÊNCIA DE ENERGIA INTERNA
Nesta situação podemos relacionar a Fext que atua sobre um objeto com
a variação da energia mecânica do objeto.
Durante seu empurrão e deslocamento de uma distância d, podemos
considerar a aceleração constante, com velocidade variando de v0 a v e a
patinadora com uma partícula desprezando o esforço de seus músculos.
K − K 0 = Fd cos θ
∆K = Fd cos θ
A situação também envolve uma variação na elevação do objeto,
podemos incluir a energia potencial
A força do lado direito dessa
∆K + ∆U = Fd cos θ Eq. não realiza W, mais é responsável
pelas variações das energias.

54. POTÊNCIA
Potência é a taxa com que uma força transfere energia de uma forma
para outra.
“Se uma certa quantidade de energia ∆E é transferida durante um
intervalo de tempo ∆t, a potência média devida à força é”
∆E
Pmed =
∆t
E a potencia instantânea
dE
P= .
dt