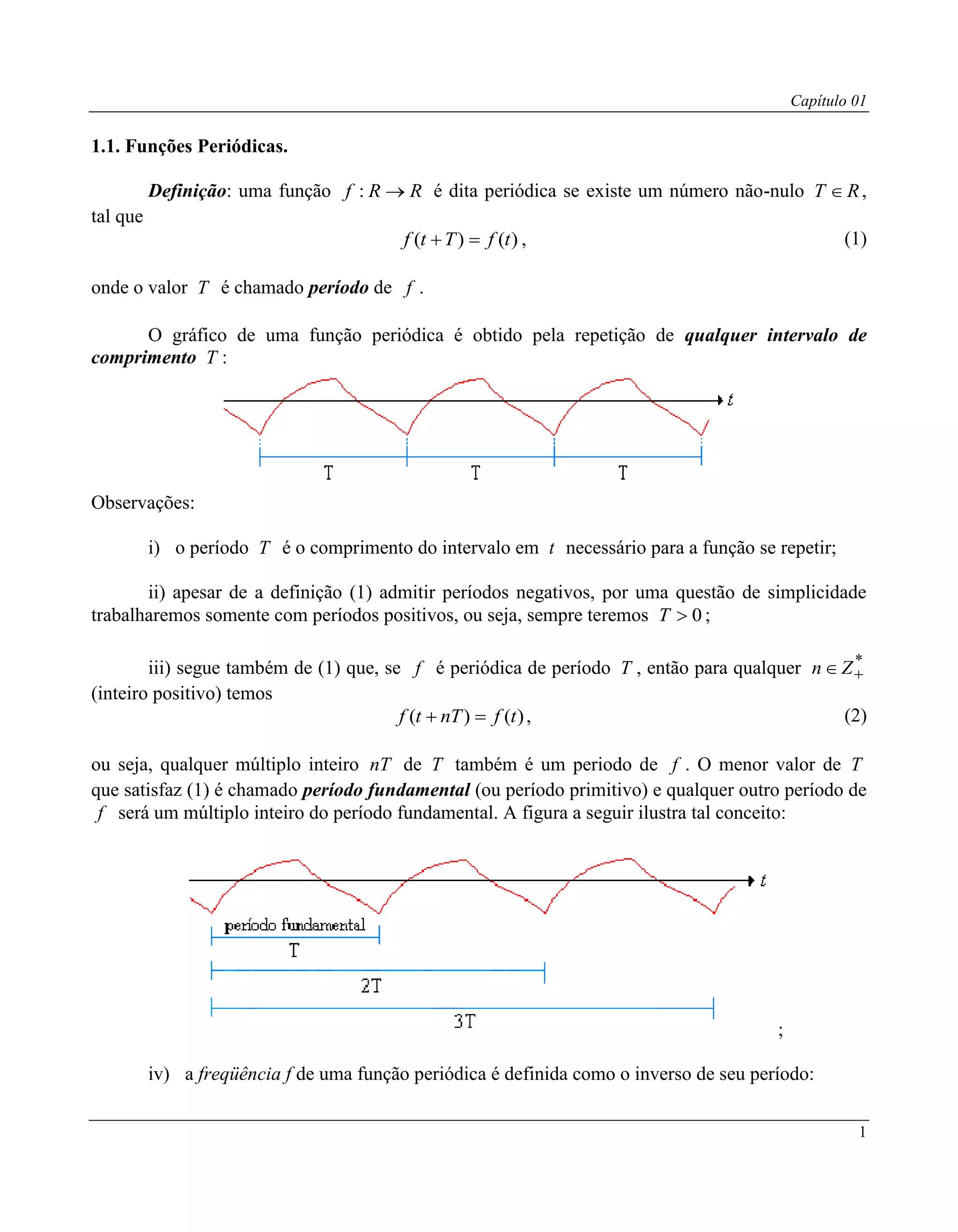
O documento apresenta conceitos fundamentais sobre funções periódicas e séries trigonométricas. Em 3 frases: 1) Define funções periódicas e apresenta suas propriedades, incluindo período fundamental e relação com frequência. 2) Explica que séries infinitas de funções periódicas podem definir novas funções periódicas e introduz séries trigonométricas. 3) Aponta que a integração de funções periódicas em intervalos de tamanho igual ao período produz o mesmo resultado, pois a área sob a cur

1. Capítulo 01
1
1.1. Funções Periódicas.
Definição: uma função RRf : é dita periódica se existe um número não-nulo RT  ,
tal que
)()( tfTtf  , (1)
onde o valor T é chamado período de f .
O gráfico de uma função periódica é obtido pela repetição de qualquer intervalo de
comprimento T :
Observações:
i) o período T é o comprimento do intervalo em t necessário para a função se repetir;
ii) apesar de a definição (1) admitir períodos negativos, por uma questão de simplicidade
trabalharemos somente com períodos positivos, ou seja, sempre teremos 0T ;
iii) segue também de (1) que, se f é periódica de período T , então para qualquer *
 Zn
(inteiro positivo) temos
)()( tfnTtf  , (2)
ou seja, qualquer múltiplo inteiro nT de T também é um periodo de f . O menor valor de T
que satisfaz (1) é chamado período fundamental (ou período primitivo) e qualquer outro período de
f será um múltiplo inteiro do período fundamental. A figura a seguir ilustra tal conceito:
;
iv) a freqüência f de uma função periódica é definida como o inverso de seu período:

2. Fabiano J. Santos
2
T
1
 ,
e nos dá o número de repetições (ciclos) em cada intervalo unitário em t . Se t é medido em
segundos então a freqüência  é o número de ciclos por segundo (Hertz). Um outro tipo de
freqüência utilizada é a freqüência angular, dada por 2;
v) o inverso do período fundamental é chamado freqüência fundamental.
Exemplo 01: a função )sen(ty  é periódica com período fundamental 2T e período n2
(n inteiro positivo), conforme ilustra o gráfico
Exemplo 02: a função )cos(ty  é periódica com período fundamental 2T e período n2
(n inteiro positivo), conforme ilustra o gráfico

3. Capítulo 01
3
Exemplo 03: a função constante ctfy  )( tem como período qualquer valor 0T , e não
possui período fundamental.
As duas proposições a seguir nos dão duas propriedades importantes das funções periódicas,
as quais utilizaremos freqüentemente.
Proposição 01: seja f uma função periódica de período T , então:
i) )(atf , 0a , é periódica de período
a
T
;
ii) )(
b
t
f , 0b , é periódica de período bT .
Provas:
i) ).()]([)( **
aTatfTtafatf 
Fazendo atu  , obtemos )()( *
aTufuf  . Logo pela hipótese concluímos que
TaT *
donde
a
T
T *
.
ii) )()](
1
[)(
*
*
b
T
b
t
fTt
b
f
b
t
f  .
Fazendo
b
t
u  , obtemos )()(
*
b
T
ufuf  . Logo pela hipótese concluímos que T
b
T

*
donde bTT *
.
Proposição 02: sejam f e g duas funções periódicas com o mesmo período T e a e b duas
constantes reais quaisquer. A função h definida por
)()()( tbgtafth  , (3)
também é periódica de período T .
Prova: aqui a prova é muito simples e pode ser obtida diretamente de (3), a saber
)()()()()()( thtbgtafTtbgTtafTth  .

4. Fabiano J. Santos
4
Exemplo 04: de acordo com a proposição (01) temos os seguintes exemplos:
a) )2sen( t , )2cos( t período 
b) )2sen( t , )2cos( t período 1
c) )
2
sen(
T
t
, )
2
cos(
T
t
período T
Além disto, para todo *
 Zn (inteiro positivo) temos que as funções
)
2
sen(
T
tn
e )
2
cos(
T
tn (4)
possuem ambas período T , haja vista qualquer múltiplo inteiro do período fundamental também
ser período. E pela proposição (2), a função
)
2
cos()
2
sen()(
T
tn
b
T
tn
axh

 ,
(5)
também possui período T .
Proposição 03: sejam nffff ,...,,, 321 funções periódicas de período T . Então a função
)(...)()()()( 321 tftftftfth n , (6)
dada pela combinação linear de nffff ,...,,, 321 também é periódica de período T . A prova é
análoga à da proposição (02) e pode ser obtida pelo princípio da indução.
1.2. Séries Trigonométricas.
Extrapolando a proposição (03), sejam ,...,...,,, 321 nffff funções periódicas de mesmo
período T , a série infinita dada por
...)(...)()()( 321  tftftftf n , (7)
define, nos pontos onde converge, uma função periódica de mesmo período T . Assim podemos
definir a função
...)(...)()()()( 321  tftftftfth n , (8)
tal que

5. Capítulo 01
5
)()( Tthth  . (9)
Esta última afirmação será de crucial importância para nosso trabalho posterior, uma vez que
trabalharemos com séries infinitas da forma


1
)
2
cos()
2
sen(
n
T
tn
T
tn 
...)
2
cos()
2
sen(...)
2
cos()
2
sen( 
T
tn
T
tn
T
t
T
t 
(10)
denominada série trigonométrica. Observe que cada termo da série em (10) possui período T ,
desta forma, nos pontos onde a série converge ela define uma função periódica de período T .
Para conveniência nos cálculos, a partir de agora consideraremos LT 2 , onde L é
chamado meio-período. Com esta convenção a equação (10) torna-se


1
)cos()sen(
n
L
tn
L
tn 
...)cos()sen(...)cos()sen( 
L
tn
L
tn
L
t
L
t 
(11)
que será nossa forma trabalhável nos próximos capítulos.
Problemas:
1. Determine se cada uma das funções a seguir é ou não períódica. Caso seja determine também seu
período fundamental T e o meio-período L .
a) )sen(
T
t
b) )cos( t c) )2senh( t d) )tan( t
e) 2
t f) )5sen( t g) )cos(mt h) t
e
i) )5sen()4sen()3cos( ttt  j) )
13
4
cos()
11
sen()
7
2
sen()
3
cos(
tttt

k) ,...3,2,1,0,
122,1
212,0
)( 





 n
ntn
ntn
tf
(sugestão: esboce o gráfico para alguns valores de n)
l) ,...3,2,1,0,
122,1
212,)1(
)( 






 n
ntn
ntn
tf
n
02*. Seja RRg : uma função periódica de período T e integrável em toda a reta R . Mostre
que

6. Fabiano J. Santos
6



Tb
b
Ta
a
dttgdttg )()(
(ou seja, não importa em qual intervalo se dá a integração o valor será sempre o mesmo desde que o
tamanho deste intervalo seja o próprio período da função. Geometricamente isto é óbvio. Por quê?)