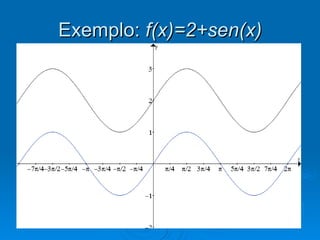
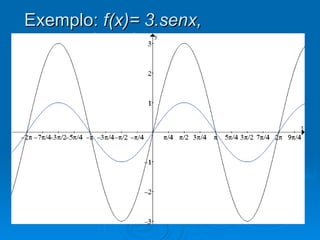
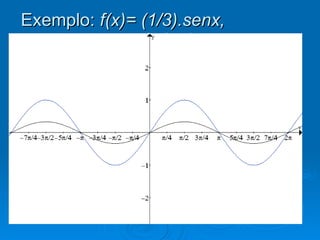
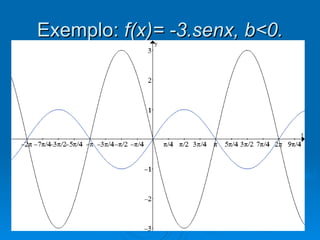
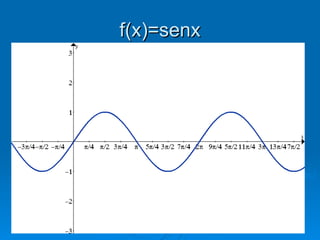
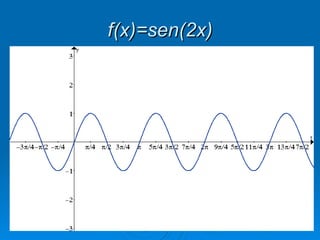
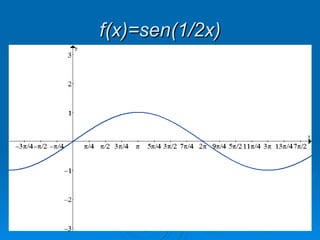
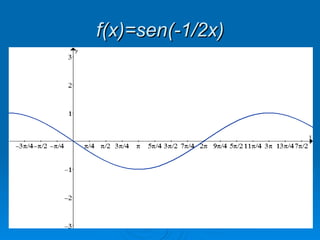
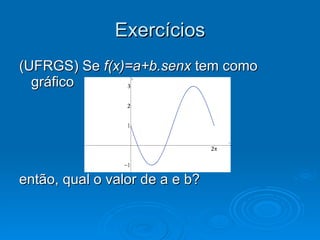
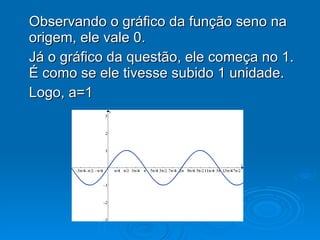
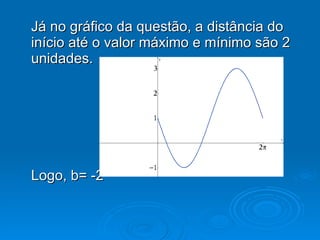
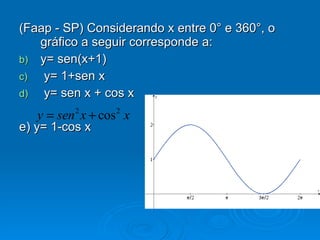
1) O documento discute funções trigonométricas na forma a + bsen(cx + d), onde a, b, c e d são constantes. 2) Os valores de a e b alteram os valores de y, enquanto c e d alteram os valores de x. 3) O valor de c altera o período da função, esticando ou esmagando a função na horizontal.

1. Funções Trigonométricas Casos Gerais

2. As funções do tipo trigonométricas são escritas na forma a, b, c e d são constantes, com b e c diferentes de zero. trig é uma das funções estudadas

3. Exemplos

4. Gráficos Os valores de a e b alteram os valores de y. O valor de a faz com que o gráfico “suba”, para a>0, e “desça”, para a<0, | a| unidades

5. Exemplo: f(x)=2+sen(x)

6. O valor de b “esmaga” ou “estica” a função na vertical Se b>0, estica Se 0<b<1, esmaga Se b<0, fica simétrico em relação ao eixo x, ou seja, troca de posição e estica.

7. Exemplo: f(x)= 3.senx, b maior que zero.

8. Exemplo: f(x)= (1/3).senx, 0<b<1.

9. Exemplo: f(x)= -3.senx, b<0.

10. Os valores de c e d alteram os valores de x. A constante c altera o período da função, ou seja, “estica” ou “esmaga” a função na horizontal . C>0, esmaga a função 0<c<1, estica C<0, simétrica em relação ao eixo do x

11. f(x)=senx

12. f(x)=sen(2x)

13. f(x)=sen(1/2x)

14. f(x)=sen(-1/2x)

15. Para calcular o período de uma função qualquer basta usar Período=

16. Exemplo Calcule o período das funções

17. A constante d faz com que o gráfico ande |d/c| para: Direita, se d<0 Esquerda, se d>0

18. Exercícios (UFRGS) Se f(x)=a+b.senx tem como gráfico então, qual o valor de a e b?

19. Observando o gráfico da função seno na origem, ele vale 0. Já o gráfico da questão, ele começa no 1. É como se ele tivesse subido 1 unidade. Logo, a=1

20. A primeira concavidade da função seno é voltada para baixo. Já no gráfico, ela é voltada para cima, ou seja, houve uma translação em relação ao eixo do x. Quando isso acontece é porque o b é negativo. Agora, qual o valor de b?

21. Analisando a função seno novamente, a distância do começo do gráfico (x=0) até o valor máximo e mínimo é 1. O que é lógico porque f(x)=senx=1.senx

22. Já no gráfico da questão, a distância do início até o valor máximo e mínimo são 2 unidades. Logo, b= -2

23. (Faap - SP) Considerando x entre 0° e 360°, o gráfico a seguir corresponde a: y= sen(x+1) y= 1+sen x y= sen x + cos x e) y= 1-cos x

24. A dúvida é: a função é seno ou cosseno? A única alternativa que traz cosseno o valor de b vale -1 e a=1. O que não é verdade. Sabemos pelas alternativas que a função é a seno.

25. O período não mudou, logo c=0. A distância do começo do gráfico até seus pontos de máximo e mínimo é 1, logo a=1. Em relação ao eixo do x o gráfico do seno não andou, logo d=0. Assim, f(x)=1+sen x. Alternativa: b