1) O documento descreve o cálculo de seno e cosseno de um ângulo x. É encontrado que sen(x)=3/5 e cos(x)=4/5. 2) Explica como modificar a amplitude e frequência de funções do tipo sen(x) multiplicando e dividindo o argumento x. 3) Resolve duas questões sobre período e conjunto imagem de funções do tipo sen(x) e cos(x).

1.  Por semelhança, podemos dizer que a altura de x é igual a 3/5.
Projetando essa altura no eixo Seno, verificamos que altura de x = Sen(x).
Assim, concluímos que Sen(x) = 3/5.
 Ao traçarmos a diagonal do retângulo localizado entre 0 e π/2,
obteremos obteremos um triângulo retângulo de hipotenusa = 1.
Sabendo o valor da hipotenusa (1) e o valor de Seno (x) (3/5), pelo teorema de
Pitágoras podemos encontrar o valor do segundo cateto, que nada mais é do
que o Cos (x). Hip2 = Sen2 + Cos2  1 = 9/25 + Cos(x)2 
 Cos(x)2 = 1 – 9/25  Cos(x)2 = 16/25  Cos(x) = √16/√25 
Assim, concluímos que Cos(x) = 4/5

3. Observe que o gráfico abaixo representa Sen(x)
Agora, compare com 3sen(x)  quando multiplicamos por 3, o gráfico aumenta
3 unidades na vertical
Então, compare com 3sen (4x)  Além do gráfico aumentar 3 unidades na
vertical, vai aumentar a freqüência em 4 vezes

4. Trata-se da função 10Sen(x/5)  Observe que a amplitude (altura) do gráfico
aumentou em 10 vezes e a freqüência diminuiu 5 vezes, ou seja, onde cabiam
5 ciclos, agora cabem somente 1: intervalo entre 0 e 5π.
Aula 22
Questão 1- Qual é o período e a imagem da função f(x) = 3 + 4 sen 푥
3
? Faça um
esboço do gráfico da função.

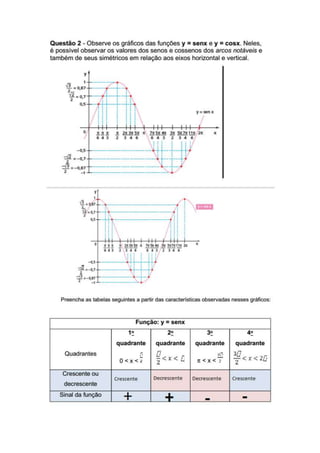
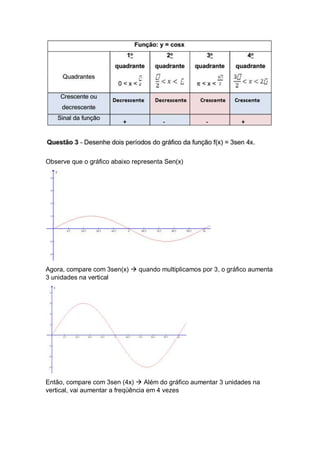
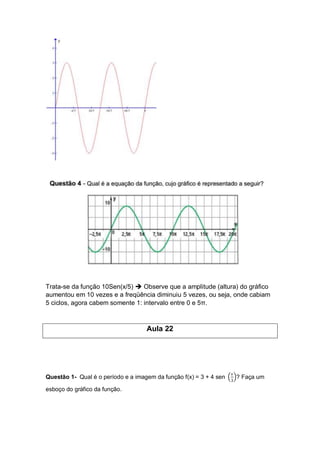
5. Para o cálculo do período da função sen(x) importa saber o coeficiente do “x”. O
período da função a + b.sen(rx+q) pode ser calculado como: 2π/r.
Como na função dada r = 1/3, temos que o período da referida função f(x) = 3 + 4
sen 푥
3
gráfico é 2π/1/3  6π
Questão 2 - Suponha a existência de um fenômeno que ocorra regularmente, de
tempos em tempos, mantendo suas características, envolvendo uma grandeza M
variando ao longo do tempo t. Nessas condições, esse fenômeno é periódico e, vamos
supor, que a intensidade da grandeza M (medida em centímetros) varie em função do
tempo t (dado em minutos) de acordo com a equação:
푀 = 3 + 2,6 cos
휋
2
푡
Determine o período e a imagem dessa função
Tempo “t” Valor de “M”
0 5,6
1 3
2 0,4
3 3
4 5,6
5 3
Podemos observar que a repetição ocorre a partir do minuto 4, ou seja, o ciclo
recomeça a cada quadro minutos. Logo, o período da função é 4 minutos.
O conjunto imagem é [0,4 ; 5,6], ou seja, está entre 0,4 e 5,6.