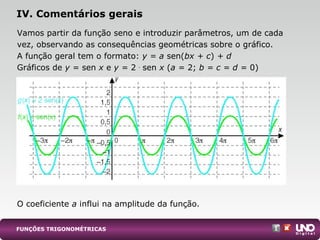
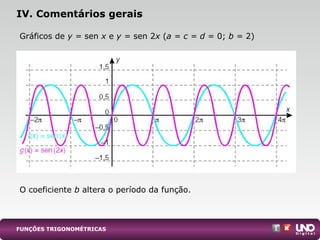
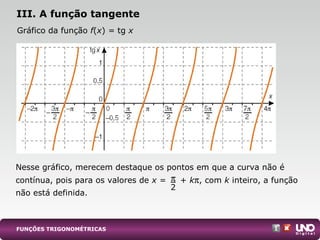
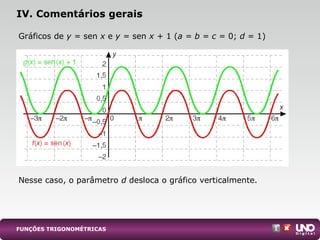
I. As funções trigonométricas são utilizadas para modelar fenômenos periódicos na natureza, com conceitos como amplitude e período permitindo aplicações em diversas áreas. II. O documento descreve as funções seno, cosseno e tangente, definindo-as geometricamente e explicando suas propriedades gráficas como intervalo de variação, período e deslocamentos. III. Variações nos parâmetros de uma função trigonométrica geral influenciam seu gráfico, modificando amplitude, período ou deslocando

1. FUNÇÕES TRIGONOMÉTRICAS
O que você deve saber sobre
As funções trigonométricas são muito úteis na modelagem de
fenômenos periódicos observados na natureza. Conceitos como
amplitude e período, além das transformações possíveis em seus
gráficos, permitem aplicações na astronomia, na geografia, na
medicina e em inúmeros outros campos do conhecimento humano.

2. FUNÇÕES TRIGONOMÉTRICAS
É definida como a relação
f: → que associa a cada valor
real x um valor real y = sen x,
correspondente à coordenada yC do
ponto C, extremidade dos arcos
côngruos a x na circunferência
trigonométrica, de tal modo que:
I. A função seno

3. Gráfico de f(x) = sen x
Para valores do domínio 0 e 2π (1a
volta positiva no centro), a
função sen x assume todos os valores reais no intervalo [–1, 1].
Esse comportamento se repete nos intervalos com extremidades
cujos calores são múltiplos inteiros de 2π.
Ex.: Em [–2π, 4π], existem seis valores de x cuja imagem vale
–0,5 (indicados no gráfico por setas vermelhas).
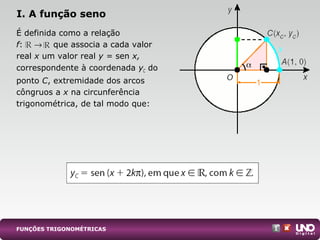
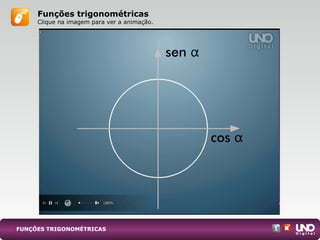
I. A função seno
FUNÇÕES TRIGONOMÉTRICAS

4. O valor 2π é chamado período da função seno, pois, a cada intervalo
correspondente a 2π percorrido no domínio, os valores de f(x)
percorrem novamente o intervalo de –1 a 1, como na 1a
volta da
circunferência, e assim sucessivamente, tanto no sentido anti-horário
da circunferência trigonométrica como no sentido horário.
Veja que f(x) = f(x + 2π) = f(x + 4π) = f(x + 6π) e assim por diante,
pois cada 2π corresponde a uma volta completa.
O intervalo de variação da imagem de y = sen x é y ∈ [–1, 1], e sua
amplitude é igual a 1, o que representa o quanto os valores de sen x
variam acima e abaixo de zero.
I. A função seno
FUNÇÕES TRIGONOMÉTRICAS

5. É definida como a relação f: →
que associa a cada valor real x
um valor real y correspondente
à abscissa xC do ponto C, extremidade
dos arcos côngruos a x
na circunferência trigonométrica,
de tal modo que:
II. A função cosseno
FUNÇÕES TRIGONOMÉTRICAS

6. I. as curvas das funções seno e cosseno têm o mesmo formato,
embora defasadas (deslocadas) unidades uma em relação a outra;
II. ambas têm amplitude igual a 1, com a imagem variando no
intervalo fechado [–1, 1];
III. ambas têm período igual a 2π.
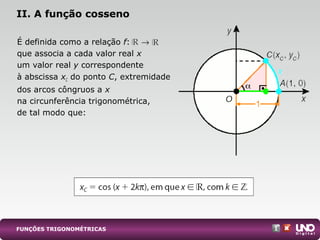
II. A função cosseno
Observe o gráfico da função y – cos x, para x ∈
FUNÇÕES TRIGONOMÉTRICAS
π
2

7. É definida como a relação f: →
que associa a cada valor real x
um valor real t, que corresponde
à ordenada do ponto T, obtido
a partir do arco x que pertence à
circunferência trigonométrica,
de tal modo que t = AT = tg x.
III. A função tangente
FUNÇÕES TRIGONOMÉTRICAS

8. Nesse gráfico, merecem destaque os pontos em que a curva não é
contínua, pois para os valores de x = + kπ, com k inteiro, a função
não está definida.
III. A função tangente
Gráfico da função f(x) = tg x
FUNÇÕES TRIGONOMÉTRICAS
π
2

9. Vamos partir da função seno e introduzir parâmetros, um de cada
vez, observando as consequências geométricas sobre o gráfico.
A função geral tem o formato: y = a sen(bx + c) + d
Gráficos de y = sen x e y = 2 .
sen x (a = 2; b = c = d = 0)
O coeficiente a influi na amplitude da função.
IV. Comentários gerais
FUNÇÕES TRIGONOMÉTRICAS

10. Gráficos de y = sen x e y = sen 2x (a = c = d = 0; b = 2)
O coeficiente b altera o período da função.
IV. Comentários gerais
FUNÇÕES TRIGONOMÉTRICAS

11. Gráficos de y = sen x e y = sen(x + 1) (a = b = d = 0; c = 1)
O parâmetro denotado pela letra c provoca uma translação
horizontal no gráfico da função.
IV. Comentários gerais
FUNÇÕES TRIGONOMÉTRICAS

12. Gráficos de y = sen x e y = sen x + 1 (a = b = c = 0; d = 1)
Nesse caso, o parâmetro d desloca o gráfico verticalmente.
IV. Comentários gerais
FUNÇÕES TRIGONOMÉTRICAS

13. FUNÇÕES TRIGONOMÉTRICAS
Funções trigonométricas
Clique na imagem para ver a animação.

14. (UFC-CE)
Considere as funções definidas f: → e g: → , respectivamente, por f(x) = x2
+ 1 e g(x) = cos x - sen x.
a) Explicite a função composta h(x) = f(g(x)).
b) Determine o valor máximo da função composta h(x) = f(g(x)).
1
FUNÇÕES TRIGONOMÉTRICAS – NO VESTIBULAR
EXERCÍCIOSESSENCIAIS
RESPOSTA:

15. O fenômeno das marés pode ser descrito por uma função da forma
f(t) = a . sen (b . t), em que a é medido em metros e t em horas. Se
o intervalo entre duas marés altas sucessivas é 12,4 horas, tendo
sempre a mesma altura máxima de 1,5 metro, então:
2EXERCÍCIOSESSENCIAIS
(PUC-Campinas-SP)
O subir e descer das marés é regulado por vários fatores, sendo o
principal deles a atração gravitacional entre Terra e Lua. Se
desprezássemos os demais fatores, teríamos sempre o intervalo
de 12,4 horas entre duas marés altas consecutivas, e
também sempre a mesma altura máxima de maré, por exemplo,
1,5 metro. Nessa situação, o gráfico da função que relacionaria
tempo (t) e altura de maré (A) seria semelhante a este:
FUNÇÕES TRIGONOMÉTRICAS – NO VESTIBULAR
RESPOSTA: A

16. (PUC-SP)
Na figura a seguir tem-se o gráfico função f, de em , definida por f(x) = k .
sen (mx), em que k e m são reais, e cujo
período é 8л.
3
5EXERCÍCIOSESSENCIAIS
FUNÇÕES TRIGONOMÉTRICAS – NO VESTIBULAR
RESPOSTA: B

17. (Unifesp)
Na procura de uma função y = f(t) para representar um fenômeno físico periódico, cuja variação total de y vai de 9,6 até
14,4, chegou-se a uma função da forma f(t) = A + B sen com o argumento medido em radianos.
8EXERCÍCIOSESSENCIAIS
RESPOSTA:a) Encontre os valores de A e B
para que a função f satisfaça
as condições dadas.
b) O número A é chamado valor
médio da função. Encontre o
menor t positivo no qual f
assume o seu valor médio.
FUNÇÕES TRIGONOMÉTRICAS – NO VESTIBULAR






−− )( 105
90
t
π

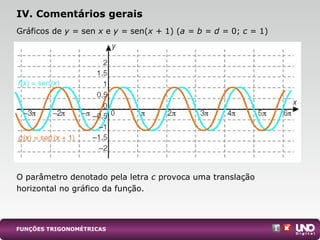
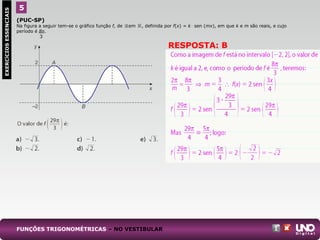
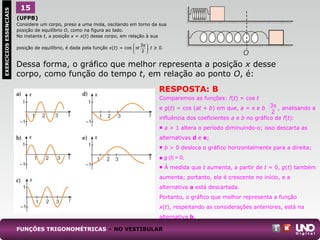
18. (Unifesp)
Considere a função y = f(x) = 1 + sen definida para todo x real
a) Dê o período e o conjunto imagem da função f.
b) Obtenha todos os valores de x no intervalo [0, 1], tais que y = 1.
1EXERCÍCIOSESSENCIAIS 12
FUNÇÕES TRIGONOMÉTRICAS – NO VESTIBULAR
RESPOSTA:





 π
π
2
2 x

19. (UFPB)
Considere um corpo, preso a uma mola, oscilando em torno da sua
posição de equilíbrio O, como na figura ao lado.
No instante t, a posição x = x(t) desse corpo, em relação à sua
posição de equilíbrio, é dada pela função x(t) = cos , t ≥ 0.
1EXERCÍCIOSESSENCIAIS 15
Dessa forma, o gráfico que melhor representa a posição x desse
corpo, como função do tempo t, em relação ao ponto O, é:
FUNÇÕES TRIGONOMÉTRICAS – NO VESTIBULAR
RESPOSTA: B
Comparemos as funções: f(t) = cos t
e g(t) = cos (at + b) em que, a = π e b , analisando a
influência dos coeficientes a e b no gráfico de f(t):
■ a > 1 altera o período diminuindo-o; isso descarta as
alternativas d e e;
■ b > 0 desloca o gráfico horizontalmente para a direita;
■ g (t) = 0;
■ À medida que t aumenta, a partir de t = 0, g(t) também
aumenta; portanto, ela é crescente no início, e a
alternativa a está descartada.
Portanto, o gráfico que melhor representa a função
x(t), respeitando as considerações anteriores, está na
alternativa b.
3π
2





 π
π
2
3
t