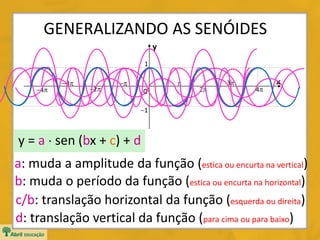
O documento descreve as funções trigonométricas seno e cosseno, definindo seus gráficos no círculo trigonométrico e propriedades como domínio, imagem e período. Também apresenta senóides, funções da forma y = a · sen(bx + c) + d, e exemplos para ilustrar como os parâmetros a, b, c e d modificam a forma da função.


![FUNÇÃO SENO
y
x
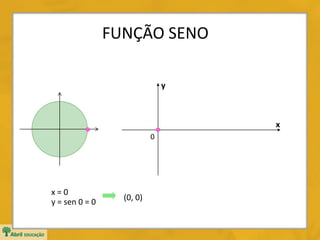
0
3
2
2
3 44
1
1
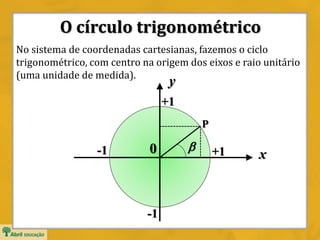
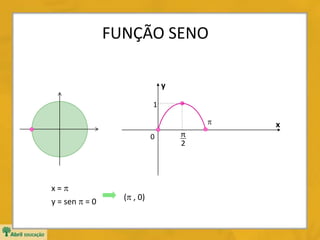
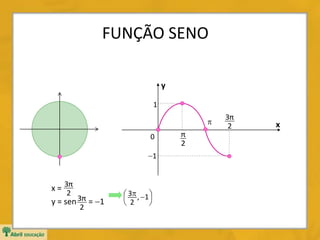
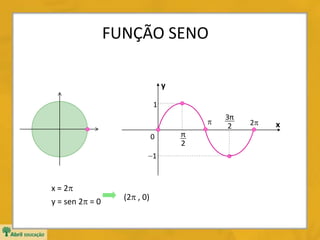
Domínio: D = IR
Imagem: Im = [1, 1]
Período: p = 2](https://image.slidesharecdn.com/funcoestrigonometricassenoides-150220140437-conversion-gate01/85/Funcoes-trigonometricas-senoides-9-320.jpg)

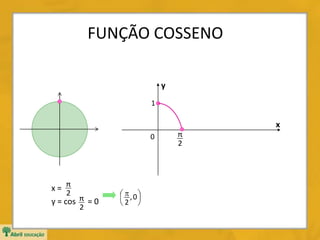
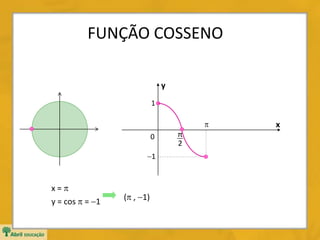
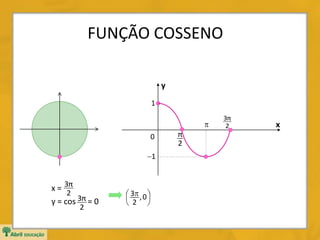
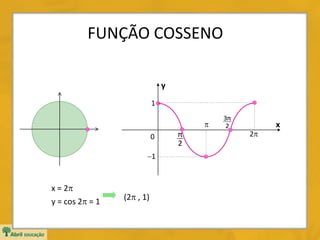
![FUNÇÃO COSSENO
y
x
0
3
2
2
3
44
1
1
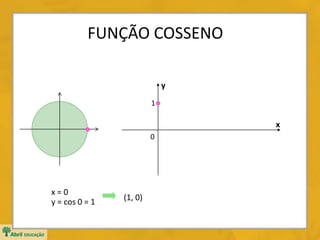
Domínio: D = IR
Imagem: Im = [1, 1]
Período: p = 2](https://image.slidesharecdn.com/funcoestrigonometricassenoides-150220140437-conversion-gate01/85/Funcoes-trigonometricas-senoides-16-320.jpg)


![EXEMPLOS DE SENÓIDES
f(x) = 2 + cos x
máximo cosseno = 1
mínimo cosseno = 1
2 + 1 = 3
2 + (1) = 1
Im = [1, 3]
IMAGEM:
DOMÍNIO: D = IR (sempre!)
Valor máximo de f(x):
Valor mínimo de f(x):](https://image.slidesharecdn.com/funcoestrigonometricassenoides-150220140437-conversion-gate01/85/Funcoes-trigonometricas-senoides-19-320.jpg)
![EXEMPLOS DE SENÓIDES
f(x) = 2 + cos x
IMAGEM:
DOMÍNIO: D = IR (sempre!)
p =
1
2
= 2
PERÍODO:
p =
b
2
p = 2
b = 1
2 + 1 = 3
2 + (1) = 1
Valor máximo de f(x):
Valor mínimo de f(x):
Im = [1, 3]](https://image.slidesharecdn.com/funcoestrigonometricassenoides-150220140437-conversion-gate01/85/Funcoes-trigonometricas-senoides-20-320.jpg)
![EXEMPLOS DE SENÓIDES
g(x) = sen 2x
máximo seno = 1
mínimo seno = 1
1
1
Im = [1, 1]
IMAGEM:
DOMÍNIO: D = IR (sempre!)
Valor máximo de g(x):
Valor mínimo de g(x):](https://image.slidesharecdn.com/funcoestrigonometricassenoides-150220140437-conversion-gate01/85/Funcoes-trigonometricas-senoides-21-320.jpg)
![EXEMPLOS DE SENÓIDES
g(x) = sen 2x
1
1
Im = [1, 1]
IMAGEM:
DOMÍNIO: D = IR (sempre!)
Valor máximo de g(x):
Valor mínimo de g(x):
p =
2
2
=
PERÍODO:
P =
b
2
p =
b = 2](https://image.slidesharecdn.com/funcoestrigonometricassenoides-150220140437-conversion-gate01/85/Funcoes-trigonometricas-senoides-22-320.jpg)
![EXEMPLOS DE SENÓIDES
h(x) = 5 3 sen (3x )
máximo seno = 1
mínimo seno = 1
5 3 1 = 2
5 3 (1) = 8
Im = [2, 8]
IMAGEM:
DOMÍNIO: D = IR (sempre!)
Valor mínimo de h(x):
Valor máximo de h(x):
Cuidado!
O sinal negativo do ( 3) “inverte o máximo e o mínimo”.](https://image.slidesharecdn.com/funcoestrigonometricassenoides-150220140437-conversion-gate01/85/Funcoes-trigonometricas-senoides-23-320.jpg)
![EXEMPLOS DE SENÓIDES
h(x) = 5 3 sen (3x )
5 3 1 = 2
5 3 (1) = 8
IMAGEM:
DOMÍNIO: D = IR (sempre!)
Valor mínimo de h(x):
Valor máximo de h(x):
p =
3
2
=
PERÍODO:
p =
b
2
p =
b = 3
3
2
3
2
Im = [2, 8]](https://image.slidesharecdn.com/funcoestrigonometricassenoides-150220140437-conversion-gate01/85/Funcoes-trigonometricas-senoides-24-320.jpg)