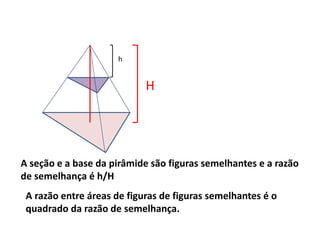
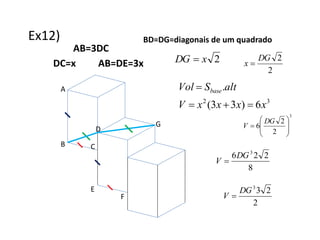
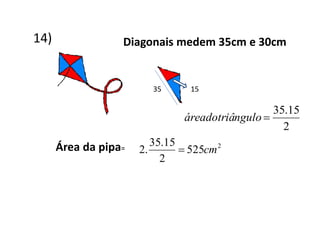
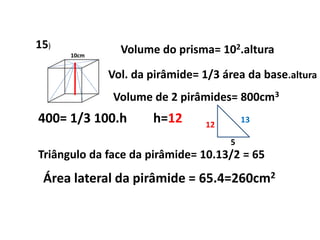
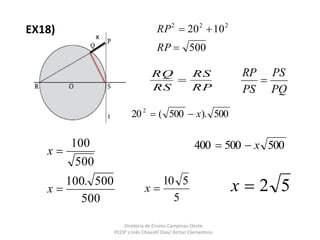
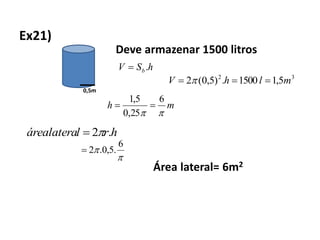
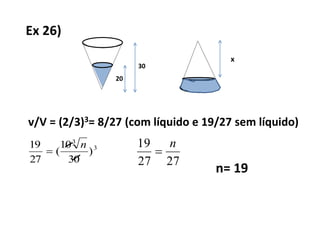
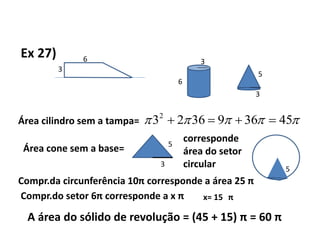
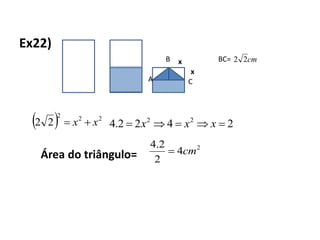
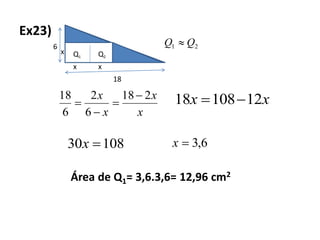
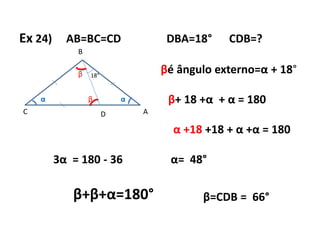
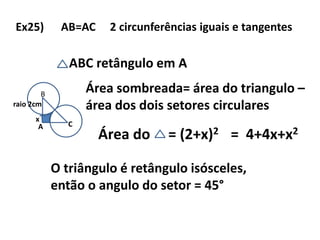
1) A razão entre a seção e a base de uma pirâmide é igual à razão de semelhança entre elas. A razão entre as áreas de figuras semelhantes é o quadrado da razão de semelhança. 2) Para resolver problemas geométricos envolvendo triângulos, razões entre lados e ângulos, é necessário aplicar propriedades como semelhança, teorema de Pitágoras e relações trigonométricas. 3) O documento apresenta vários exercícios resolvidos de geometria plana e

1. RESOLUÇÕES DE
EXERCÍCIOS

3. h
H
A seção e a base da pirâmide são figuras semelhantes e a razão
de semelhança é h/H
A razão entre áreas de figuras de figuras semelhantes é o
quadrado da razão de semelhança.

4. Ex12)
A
B C
D
F
E
G
AB=3DC
DC=x AB=DE=3x
BD=DG=diagonais de um quadrado
2xDG 
2
2DG
x 
32
6)33(
.
xxxxV
altSVol base


3
2
2
6 








DG
V
8
226 3
DG
V 
2
233
DG
V 

5. 14) Diagonais medem 35cm e 30cm
35 15
2
15.35
nguloáreadotriâ
Área da pipa= 2
525
2
15.35
.2 cm

6. 10cm
Volume do prisma= 102.altura
Vol. da pirâmide= 1/3 área da base.altura
Volume de 2 pirâmides= 800cm3
400= 1/3 100.h h=12 12
5
13
Triângulo da face da pirâmide= 10.13/2 = 65
Área lateral da pirâmide = 65.4=260cm2
15)

7. Diretoria de Ensino Campinas-Oeste
PCOP´s:Inês Chiarelli Dias/ Airton Clementino
RP
RS
RS
RQ

x
500
1020 222


RP
RP
500).500(202
x
500500400 x
500
500.100
500
100


x
x
5
510
x 52x
EX18)
PQ
PS
PS
RP


8. Ex21)
0,5m
Deve armazenar 1500 litros
hSV b.
32
5,11500.)5,0(2 mlhV  
mh

6
25,0
5,1

hrlárealatera .2


6
.5,0.2
Área lateral= 6m2

9. Ex22)
CA
B BC= cm22x
x
  222
22 xx  2422.4 22
 xxx
Área do triângulo=
2
4
2
2.4
cm

10. Ex23)
Q1 Q2
6
18
21 QQ 
x
x x
x
x
x
x 218
6
2
6
18 


 xx 1210818 
10830 x 6,3x
Área de Q1= 3,6.3,6= 12,96 cm2

11. Ex 24) AB=BC=CD DBA=18° CDB=?
A
B
C D
18°
αα
β
β
βé ângulo externo=α + 18°
β+ 18 +α + α = 180
α +18 +18 + α +α = 180
3α = 180 - 36 α= 48°
β+β+α=180° β=CDB = 66°

12. Ex25) AB=AC 2 circunferências iguais e tangentes
A
B
C
ABC retângulo em A
raio 2cm
Área sombreada= área do triangulo –
área dos dois setores circulares
Área do = (2+x)2
x
= 4+4x+x2
O triângulo é retângulo isósceles,
então o angulo do setor = 45°

13. Ex 26)
30
20
x
v/V = (2/3)3= 8/27 (com líquido e 19/27 sem líquido)
3
3
)
30
10
(
27
19 n

2727
19 n

n= 19

14. Ex 27) 6
3
5
6
3
3
Área cilindro sem a tampa=  4536936232

Área cone sem a base=
3
5
corresponde
área do setor
circular 5
Compr.da circunferência 10π corresponde a área 25 π
Compr.do setor 6π corresponde a x π x= 15 π
A área do sólido de revolução = (45 + 15) π = 60 π

15. Ex28)
2
Área do quadrado(4 setores
de 45°+ área sombreada)= 16
Área do setor= ¼ área do círculo= ¼ π.22=π
Área da região sombreada = 16 - 4π

17. 2
6
 3
3
6
hv
V
 86.2.
3
1 2
V
3
3
6
4
8
h



3
216
2
h
 3
108h cmh 3
43

18. • Um recipiente cilíndrico reto, com raio da base
medindo 6 cm, contém água até metade de sua
altura. Uma esfera maciça,colocada no seu
interior, fica totalmente submersa, elevando a
altura da água em 1 cm. O raio da esfera mede,
em centímetros,
• (A) 1,5
• (B) 2
• (C) 2,5
• (D) 3
• (E) 3,5

19. 6
h/2
1
2

h
hV
h
V 

18
2
.6. 2







 1
2
6. 2 h
V   36.18  hV
Volume após subir 1cm na altura
A diferença entre os volumes 36π= volume da esfera
 36.
3
4
.
3
4 33
 rrVesf 27
4
3.363
r
Raio da esfera=3cm