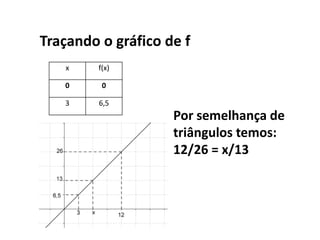
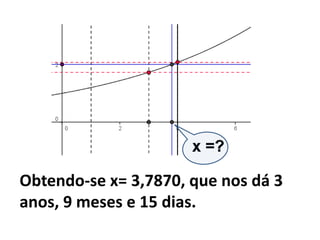
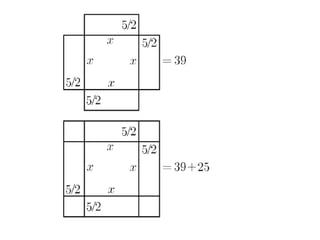
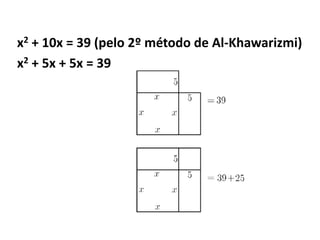
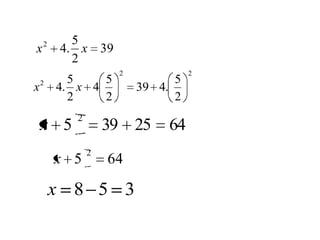O documento discute a história da resolução de equações ao longo dos séculos, desde os egípcios até os árabes. Os egípcios resolviam equações de forma complexa através de métodos geométricos. Os árabes progrediram na resolução de equações ao denominar o valor desconhecido de "coisa", dando origem ao símbolo x. O Papiro de Rhind, do antigo Egito, contém os primeiros registros de equações na forma escrita, resolvidas por métodos como a "regra da falsa posição".

4. “Assim como o Sol empalidece
as estrelas com o seu
brilho, um homem inteligente
eclipsa a glória de outro
homem nos concursos
populares, resolvendo os
problemas que este lhe
propõe”. François Viète

5. Esse texto da Índia antiga fala de um
passatempo muito popular dos
matemáticos hindus da época: a solução
de quebra cabeças em competições
públicas, em que o competidor propunha
problemas para outro resolver. Sem
nenhum sinal, sem nenhuma variável,
somente alguns poucos sábios eram
capazes de resolver problemas, usando
muitos artifícios e trabalhosa construções
geométricas.

6. Os egípcios não utilizavam notação
algébrica, os métodos de solução de uma
equação eram complexas e cansativos.
Os gregos resolviam equações através de
Geometria.
Foram os árabes que, cultivando a
Matemática dos gregos, conseguiram
progresso na resolução de equações.
Chamavam o valor desconhecido de “coisa”,
pronunciada como xay, daí surge o x como
tradução simplificada de palavra “coisa”.

7. Equações do primeiro grau
Do ponto de vista elementar, equações
são problemas que determina certos
valores desconhecidos, sabendo que
quando esses valores são
manipulados algebricamente, de uma
certa maneira, são obtidos certos
valores dados. As primeiras
equações na forma escrita surgiram
no antigo Egito 3000 anos a.C.

8. Há aproximadamente 3600 anos o
faraó do Egito tinha um súdito cujo
nome chegou até os nossos dias:
Aahmesu, cujo significado é “filho da
lua”, era uma pessoa muito simples
provavelmente um escriba.
Atualmente ele é conhecido como
Ahmes autor do Papiro Ahmes, mais
famoso como Papiro de Rhind.

9. O Papiro de Rhind foi encontrado em
meados do século passado,
presumivelmente nas proximidades do
templo de Ramsés II, na antiga cidade
de Tebas, no Egito. Em 1858 foi
comprado, no local, pelo antiquário
escocês A.H. Rhind .
O papiro é um rolo com cerca de 30cm
de altura e 5m de comprimento e
encontra-se hoje, salvo alguns
fragmentos, no Museu Britânico.

10. O Papiro de Rhind é um antigo manual
de Matemática, contendo 80
problemas de Álgebra, cada um com a
sua solução.
Nesse papiro, encontramos as primeiras
equações do primeiro grau, na forma
de problemas “aha. Aha significava
quantidade. Tais problemas referem-
se à determinação de quantidades
desconhecidas.

11. Fragmento do Papiro de Rhind – Museu Britânico

12. Problemas aha do Papiro RHIND
(Prob24) Uma quantidade e seu sétimo,
somadas juntas, dão 19, Qual é a
quantidade?
(Prob25) Uma quantidade e sua metade,
somadas juntas, resultam 16. Qual é a
quantidade?
(Prob28) Uma quantidade e os seus dois
terços são adicionados, e da soma um
terço da soma é subtraído e ficam 10.Qual
é a quantidade?

13. Mais um problema:
“Um montão, seus dois terços, sua
metade, todos ao juntar-se fazem treze.
Qual é a quantidade?”
O problema se reduz a essa equação:

14. Regra da “falsa posição”
Para os antigos matemáticos egípcios
suas equações vinham expressas
totalmente em palavras, a álgebra
puramente simbólica estava muito
distante de ser inventada.
Encontravam a solução deste tipo de
equação através de um método
chamado regra da falsa posição.

15. - Atribuíam um valor falso a montão, por
ex 12:

16. Onde se conclui que o valor falso 12 está
para 26 assim como o valor verdadeiro =
montão está para 13.
montão = 6
Utilizou-se uma “regra de 3 simples”

17. Por que uma regra de 3 simples dá o valor
verdadeiro de x? Coincidência?
Através da idéia moderna de função :
“Se f é uma função cujos valores são dados
pela fórmula , para que
valor de x temos f(x) = 13?”

18. Traçando o gráfico de f
x f(x)
0 0
3 6,5
Por semelhança de
triângulos temos:
12/26 = x/13

19. Após ser achado 26 como solução,
poderia ser aplicado o fator de correção,
13/26, no valor suposto 12.

21. Vamos resolver os três problemas
anteriores pela “regra da falsa
posição”.
Desafio:
“ Doze anéis de prata pesam tanto
quanto oito anéis de ouro. Se trocarmos
um anel de prata por um anel de ouro, a
diferença será de 6 tzin. Digam-me,
quanto pesa um anel de prata e um anel
de ouro?”

22. 12p = 8o 12p – 1p + 1o = 7o + 1p + 6tzin
11p + 1o = 7o + 1p + 6 10p – 6o = 6
supondo p = 2 e o = 3, teremos
10.2 – 6.3 = 20 – 18 = 2
solução deveria ser 6 solução foi 2
Aplicando o fator de correção (falso montão
p=2 e o =3)
Anel de prata = 6,
anel de ouro = 9

23. Regra da “ dupla falsa posição”
A regra anterior resolve equações do
tipo ax = b, mas para solucionar
equações do tipo ax + b =c, a regra não
funciona.
Supostamente, já antes de Cristo, os
babilônios e os chineses usavam neste
caso, a regra da “dupla falsa posição”.

24. Para achar x tal que ax + b =c, atribui-se
dois valores “falsos” x1 e x2.
Se d1 = ax1 + b – c e d2 = ax2 + b – c, a
proporção
=

25. A regra, em linguagem de hoje, se
f(x)=ax +b

26. Uma outra versão da mesma regra:
Para problemas não lineares a regra
poderá dar soluções aproximadas.
Esse problema não linear, foi
encontrado entre os escritos dos antigos
babilônicos. Nele se pergunta em
quantos anos duplica um capital de 1
gur, a juros de 20% ao ano

27. Em notação de hoje:
Após 3 anos o capital ficará
multiplicado por (1,2)3
Após 4 anos o capital ficará
multiplicado por (1,2)4
Se usarmos a fórmula temos
x1=3 f(x1) = 1,728, x2=4 f(x2) = 2,0736

28. Obtendo-se x= 3,7870, que nos dá 3
anos, 9 meses e 15 dias.

29. Já no século XVI, Cardano usa a regra
da falsa posição, repetidas vezes em
um mesmo problema, a fim de obter
melhores aproximações para a
solução.
Atualmente usamos tal regra, com o
nome e Interpolação Linear, para
aproximarmos um arco de curva por
segmento de reta

30. O homem que calculava Cap V
Beremiz resolve um problema e
determina a dívida de um joalheiro.
... – Esse homem (e apontou para o
joalheiro) veio da Síria vender jóias em
Bagdá; prometeu-me que pagaria, pela
hospedagem, 20 dinares se vendesse as
jóias por 100 dinares, pagando 35 se as
vendesse por 200. Ao cabo de vários
dias, acabou vendendo tudo por 140
dinares.

31. Proporção feita pelo mercador de jóia:
200 está para 35, assim como 140 está
para x. Total da dívida 24,5.
Proporção feita pelo dono da
hospedaria: 100 está para 20, assim
como 140 está para x. Total da dívida 28.
Quem está certo?

32. A explicação de Beremiz :
A diferença de 100, no preço da
venda, corresponde a uma diferença de
15 no preço da hospedagem.
Se um acréscimo de 100 na venda traria um
aumento de 15 na hospedagem, eu
pergunto: Qual será o aumento da
hospedagem para acréscimo de 40 na
venda? Se a diferença fosse de 20 (que é
1/5 de 100), o aumento da hospedagem

33. seria de 3 (pois 3 é 1/5 de 15). Para a
diferença de 40 (que é o dobro de 20), o
acréscimo da hospedagem deverá ser de
6. O pagamento correspondente a
140, é, portanto, de 26.
.....

34. De uma forma resumida, podemos
dizer que quando temos uma função
qualquer, dois valores de seu domínio:
x1 e x2 e suas respectivas imagens f(x1) e
f(x2), se desejarmos obter o valor
x, compreendido entre x1 e x2 e que
tenha imagem (f(x)=c) compreendida
entre f(x1) e f(x2), podemos aplicar a
interpolação linear através da relação.

35. f(20) = 100 e f(35) =200, ou seja x1 = 20 e
f(x1) = 100; x2 = 35 e f(x2) = 200, como as
jóias foram vendidas por 140 dinares,
temos que c=f(x)=140 e desejamos obter
o valor correspondente a x, ou seja:
Resolvendo essa proporção, obtemos
x=26, que são os 26.

36. Problemas de balanceamento de
misturas
1) Um técnico de laboratório tem duas
soluções de ácido sulfúrico (solução ácida=
água destilada + ácido). A primeira é 30%
ácida e a segunda é 70% ácida. Quantos
mililitros de cada ele deve usar para obter
200 ml de uma solução 60% ácida?

37. Serão utilizadas x ml da sol. de 30% ácida e
y ml da sol. 70% ácida. A solução
resultante será de 200 ml e 60% ácida.
Daí :
x ml + y ml = 200 ml
30% de x ml + 70% de y ml = 60% de 200 ml
x + y = 200
0,3x + 0,7 y = 0,6. 200
Tudo se reduz a uma equação do 1º grau ao
substituir y = 200 – x

38. 2) Que volume de álcool deve ser
adicionado a 600 litros de uma solução
15% alcoólica (solução alcoólica = álcool +
água) de modo que a solução resultante
seja 25% alcoólica?
Em 600 litros temos 15% de álcool = 90 litros
de álcool, logo 510 litros de água que
corresponde a 85% .

39. Queremos que esses 510 litros
corresponda a 75% da solução ( solução
resultante 25% de álcool).
Adicionar 80 litros de álcool

40. O Banho de Arquimedes
Arquimedes de Siracusa foi um grande físico e
matemático grego do séc. 3 a.C.,pesquisador da
“Universidade” de Alexandria, cidade do antigo
Egito fundada por Alexandre o Grande às
margens do Rio Nilo.
Conta uma lenda que o rei Hierão de Alexandria
suspeitava que sua coroa não teria sido feita de
ouro puro, mas sim de uma mistura (liga) de
ouro e prata, e incumbiu Arquimedes de calcular
as quantidades desses metais empregadas na
confecção da coroa.

41. Arquimedes descobriu um meio de fazer
isso enquanto se banhava. Celebrando a
descoberta, saiu às ruas gritando
Eureka! (Descobri!), tendo no entanto se
esquecido de vestir-se ao sair.

42. Algumas considerações:
A densidade de um corpo material não oco é a
razão entre sua massa e seu volume. Por ex. a
densidade do mel é 1300g por litro; 1,3g/cm3.
densidade = massa/volume, logo
volume = massa/densidade.
Por ex. o volume de 1kg de mel é dado por
Volume = 1kg/1,3kg/l ≅ 769ml

43. A massa de um corpo é uma quantidade
calculável por comparação com outra
massa, balança de dos pratos.
O volume do corpo , desde que não seja
esponjoso, pode ser determinado por
imersão deste corpo num tanque de água.
Uma coroa de m gramas de uma liga de ouro
e prata. Deseja-se determinar a quantidade
de x gramas de ouro e a quantidade de y
gramas de prata presentes nessa liga.

44. volume do ouro = massa do ouro /
densidade do our.
Densidade do ouro = 19,3g/cm3
Densidade da prata = 10,5 g/cm3.
Volume do ouro =
Volume da prata =

45. Volume da coroa = +
Chega-se então ao sistema:
x + y =m
Supondo que a coroa do Rei Hierão, tivesse
massa de 4200g ( será que a cabeça do rei
aguenta?) e volume 268cm3. Quais as
quantidades de ouro e prata presentes nessa
coroa?
x = 3 039,75 y = 1 160,25

46. Problemas
1) Duas toneladas de uma liga metálica
contém 15% de estanho. Que quantidade
de estanho deve ser adicionada a essa
liga de modo a aumentar a concentração
de estanho a 20%?

47. 2) A densidade do ouro é de 19,3g/cm3
e a do cobre é de 8,9 g/cm3. Uma liga
de ouro e cobre tem 6 cm3 e 95g. Quais
são as quantidades de ouro e cobre
presentes na liga?

48. 3) Durante a discussão da reforma do
sistema previdenciário, na década de 1990,
aventou-se a hipótese de ser adotada, a
chamada “fórmula 95”. Segundo ela, os
trabalhadores teriam direito à
aposentadoria quando a soma do número
de anos trabalhados com a idade do
trabalhador fosse igual a 95. Com que
idade poderia, aposentar-se uma pessoa
que tivesse começado a trabalhar com 23
anos?

49. 4) Considere 3 números a, b, c. A média
aritmética entre a e b é 17 e a média
aritmética entre a, b, e c é 15. Qual é o
valor de c?

50. 5) Numa caixa, o número de moedas de
1 real é o triplo do número de moedas
de 25 centavos. Se tirarmos 2 moedas
de 25 centavos e 26 moedas de 1 real, o
número de moedas de 1 real e de 25
centavos ficará igual. Qual a quantidade
de moedas de 1 real e de 25 centavos?

51. 6) Eu tenho o dobro da idade que tu tinhas
quando eu tinha a tua idade, quando tu
tiveres a minha idade, a soma das nossas
idades será de 45 anos. Quais são as nossas
idades?

52. 7) Uma amostra de água salgada
apresenta 18% de salinidade. Isto
significa que em 100 gramas de amostra
teremos 18 gramas de água. Qual a
melhor aproximação do percentual de
água da amostra a ser evaporado se
quisermos obter 30% de salinidade?

53. Equações do segundo grau
Da Antiga Babilônia até Diofanto
Os antigos babilônios (ou babilônicos -
1800.a.C), habitantes do sul da antiga Mesopotâmia
(parte do atual Iraque), já resolviam o problema de
encontrar dois números x e y cuja soma é p e cujo
produto é q. o método empregado pelos
babilônios, traduzido para nossas notações
modernas, é basicamente o seguinte:
A priori, x e y são representados na forma:

54. Dado x + y = p . Tem-se então
de onde
Daqui, se deduz
(os números negativos ainda não haviam sido inventados).

55. Assim x e y acabam sendo expressos como
Cerca de dois milênios depois (em torno do ano
250 da era cristã), este mesmo método aparece
no tratado Arithmetica do grego Diofanto,
considerado o pai da álgebra no sentido de ter
sido o primeiro a empregar notações simbólicas
para expressões algébricas.

56. Exemplos encontrados nas tábuas de argila dos
antigos babilônios, bem como no livro
Arithmetica de Diofanto, resolvidos pelo
método exposto anteriormente.
Ex1) (Babilônios, 1800 a.C.) Encontre dois
números cuja soma é 14 e cujo produto é 45.
Ex2) (Diofanto, em Arithmetica) Encontre dois
números cuja soma é 20 e cuja soma de seus
quadrados é 208.

57. Ex3) Dois números cuja soma é 10 e cuja soma
dos seus cubos é 370.
Ex4) Encontre dois números x e y satisfazendo
x – y = 10 e x 3- y 3 = 2170
Método Diofanto: se a diferença x – y= p é
dada, escrevemos x = a + p/2 e y = a – p/2
Ex5) Encontre dois números x e y satisfazendo
x – y = 4 e x3 + y3 = 28(x + y)
Ex6) Resolva a equação x2– 6x = 27 (método
babilônico: Escreva a equação na forma
x.(x – 6) = 27

58. Ex7) Resolva a equação x2 + 6x = 16 pelo
método babilônico descrito no ex. anterior

59. AL-KHWARIZMI
O primeiro tratado a abordar sistematicamente
as equações do 2º grau e suas soluções foi Os
Elementos de Euclides (séc. 3a.C.). Em Os
Elementos, Euclides nos dá soluções
geométricas da equação do segundo grau. Os
métodos geométricos ali encontrados, embora
interessantes, não são práticos.
No início do século 9, o Califa Al
Mamum, recebeu através de um sonho, no qual
teria sido visitado pelo imortal Aristóteles, a
instrução de

60. fundar um centro de pesquisa e divulgação
científica. Tal instituição, a Casa de
Sabedoria, foi fundada em Bagdá, hoje
capital do Iraque, às margens do Rio Tigre. Lá,
a convite do Califa, estabeleceu-se Al-
Khwarizmi, juntamente com outros filósofos
e matemáticos do mundo árabe.
A pedido do Califa, Al-Khawarizmi, escreveu um
tratado popular sobre a ciência das
equações: Livro da Restauração e
Balanceamento

61. No seu trabalho, Al-Khwarizmi apresenta dois
métodos geométricos de solução da equação
do 2º grau. Al-Khwarizmi não fazia uso de
notações simbólicas em seu tratado. Sua
equações são escritas no estilo retórico, isto é,
sem o emprego de símbolos.

62. RESOLUÇÃO DA EQUAÇÃO DO 2º GRAU PELOS
MÉTODOS DE AL-KHWARIZMI
x2 + 10x = 39 (pelo 1º método de Al-
Khawarizmi)
Primeiramente a equação é escrita na forma
10
x 2 4. x 39 ou seja, x 2 4. 5 x 39
4 2

64. 2 5
x 4. x 39
2
2 2
2 5 5 5
x 4. x 4 39 4.
2 2 2
2
x 5 39 25 64
2
x 5 64
x 8 5 3

65. x2 + 10x = 39 (pelo 2º método de Al-Khawarizmi)
x2 + 5x + 5x = 39

66. x2 + 5x + 5x + 52 = 39+52
(x + 5)2 = 39+25 = 64

67. Equações do 2º grau: Os dois tipos fáceis
I) Equações do tipo: (Ax + B)2= C
Observar: C < 0 e C = 0
(3x + 1)2 = 16
II) Equações do tipo : (Ax + B) (A’x + B’) = 0
(2x + 1)(3x – 2) = 0

68. Fatorando o trinômio:
Seja o trinômio ax2+ bx + c = 0, então a ≠ 0 é
b c
equivalente x2 x 0 então sempre que for
a a
conveniente , podemos supor que a equação do 2º
grau tem a forma x2 + px + q = 0, onde p= b/a e q= c/a
Precisamos fatorar o trinômio acima para que possa
colocá-la na forma (x - ⍺ )( x - )= x2 –(⍺ + )x + ⍺𝞫 0
𝞫 𝞫 =
Para fatorar o trinômio x2 + px + q, devemos achar
números ⍺, 𝞫 que ⍺ + 𝞫 -p e ⍺ . = q.
tais = 𝞫
O problema de achar dois números conhecendo sua
soma e seu produto é muito antigo, já foi resolvido pelos
babilônicos há cerca de 4 mil anos.

69. Ex: Meu vizinho, com 20m de cerca, constituiu
um cercado retangular de 32m2 de área,
utilizando seu muro como um dos lados.
Quanto medem os lados desse retângulo?
Ex: Será que meu vizinho não poderia , ainda
usando o muro como um dos lados, fazer um
cercado retangular com 32m2 de área, porém
usando uma cerca menor?

70. Ex: Comprei algumas garrafas de um bom vinho
por 540 reais. Por ter obtido um desconto de
15 reais no preço de cada garrafa, consegui
comprar 3 garrafas a mais do que previra
originalmente. Quantas garrafas de vinho
comprei?

71. • Equações do 2º grau disfarçadas
2 3
1
x 1 x 2
x 1 3x 15

72. • http://www.matematiques.com.br/conteudo.
php?id=582
• Redefor- Ensino da Algebra Elementar através
de sua história- Prof. João Carlos V. Sampaio
• A regra da falsa posição – Oscar Guelli
• Provas Profmat
• Projeto Araribá- Ed. Moderna - 7º ano
• Desafios – Site Só Matemática
• Temas e Problemas Elementares: Elon Lages et
al
• Banco de Questões OBMEP- 2009/2010/2011