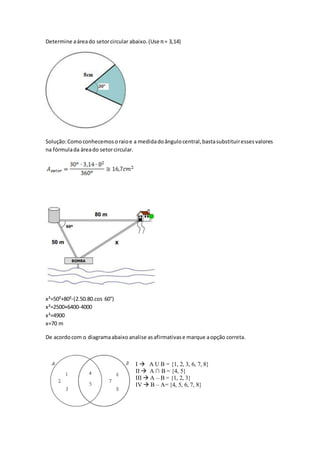
O documento apresenta vários problemas de geometria envolvendo cálculo de áreas e perímetros de figuras planas como triângulos, quadrados e setores circulares. As soluções envolvem aplicar as fórmulas apropriadas para cada caso, como a fórmula da área de um triângulo, quadrado, retângulo, trapézio ou setor circular.

1. 1) Temos um triângulo equilátero de lado 6cm. Qual é o perímetro e qual é a
área deste triângulo?
Perímetro:
6*3 = 18cm
Área:
2)Sabendo que a área de um quadrado é 36cm², qual é seu perímetro?
Vamos descobrir o lado do quadrado:
x*x = 36
x =
x = 6
Então seu perímetro é 6*4 = 24cm.
Um triângulo isósceles tem base medindo 8 cm e lados iguais com medidas de 5 cm. A
área deste triângulo é:
A( ) 20 cm2 . B( ) 10 cm2 . C( ) 24 cm2 . D( ) 18 cm2 . E( ) 12 cm2 .
Em um triângulo retângulo, a hipotenusa é 5/3 do tamanho do cateto menor. O cateto
maior tem tamanho igual a 4/3 do cateto menor. Sendo 60 cm o perímetro desse
triângulo, sua área será de:
A( ) 135 cm2 B( ) 120 cm2 C( ) 150 cm2 D( ) 100 cm2 E( ) 187,5 cm2

3. Decomposição da área em figuras conhecidas:
A área da região é constituída de um retângulo, um triângulo e um trapézio. Agora basta
determinarmos as áreas de cada figura.
Área 1 – Retângulo
O retângulo referente a área 1 possui as seguintes dimensões:

4. Sua área é calculada multiplicando o comprimento pela largura:
A = 24 * 12
A = 288 m²
Área 2 – Triângulo
A área de uma região triangular é calculada através da metade da multiplicação da base
pela altura.
A = (10*12) / 2
A = 120 / 2
A = 60 m²
Área 3 – Trapézio
A área de um trapézio é dada pela seguinte expressão: , onde:
B: base maior
b: base menor
h: altura
Então:

5. A área total da região é dada pelo somatório das áreas das regiões 1, 2 e 3:
Área total = 288m² + 60m² + 88m²
Área total = 436 m²
A figura mostra o local onde será realizado um evento cultural. Calcule a
quantidade que será arrecadada com base nas seguintes informações se os três
setores ficarem lotados:
- setor amarelo abriga quando lotado, 720 pessoas;
- o preço do ingresso varia de acordo com o setor, da seguinte forma: área
amarela = R$ 15,00, área azul = R$ 10,00 e área verde = R$ 12,00.
Determine a área da coroa circular da figura a seguir, considerando o raio da
circunferência maior igual a 10 metros e raio da circunferência menor igual a 8 metros.
A = π * (R² – r²)
A = π * (10² – 8²)
A = π * (100 – 64)
A = π * 36
A = 36π m²
ou
A = 36 * 3,14
A = 113,04 m²

6. Determine aáreado setorcircular abaixo.(Use π= 3,14)
Solução:Comoconhecemosoraioe a medidadoângulocentral,bastasubstituiressesvalores
na fórmulada áreado setorcircular.
x²=50²+80²-(2.50.80.cos 60°)
x²=2500+6400-4000
x²=4900
x=70 m
De acordocom o diagramaabaixo analise asafirmativase marque aopção correta.
I  A U B = {1, 2, 3, 6, 7, 8}
II  A ∩ B = {4, 5}
III  A – B = {1, 2, 3}
IV  B – A= {4, 5, 6, 7, 8}

7. a) Todas as afirmativassãoverdadeiras;
b) Somente asafirmativas I,II e III são verdadeiras;
c) Somente asafirmativas II e III são verdadeiras;
d) As afirmativas I, II e IV são falsas;
e) Somente a afirmativa II é verdadeira.