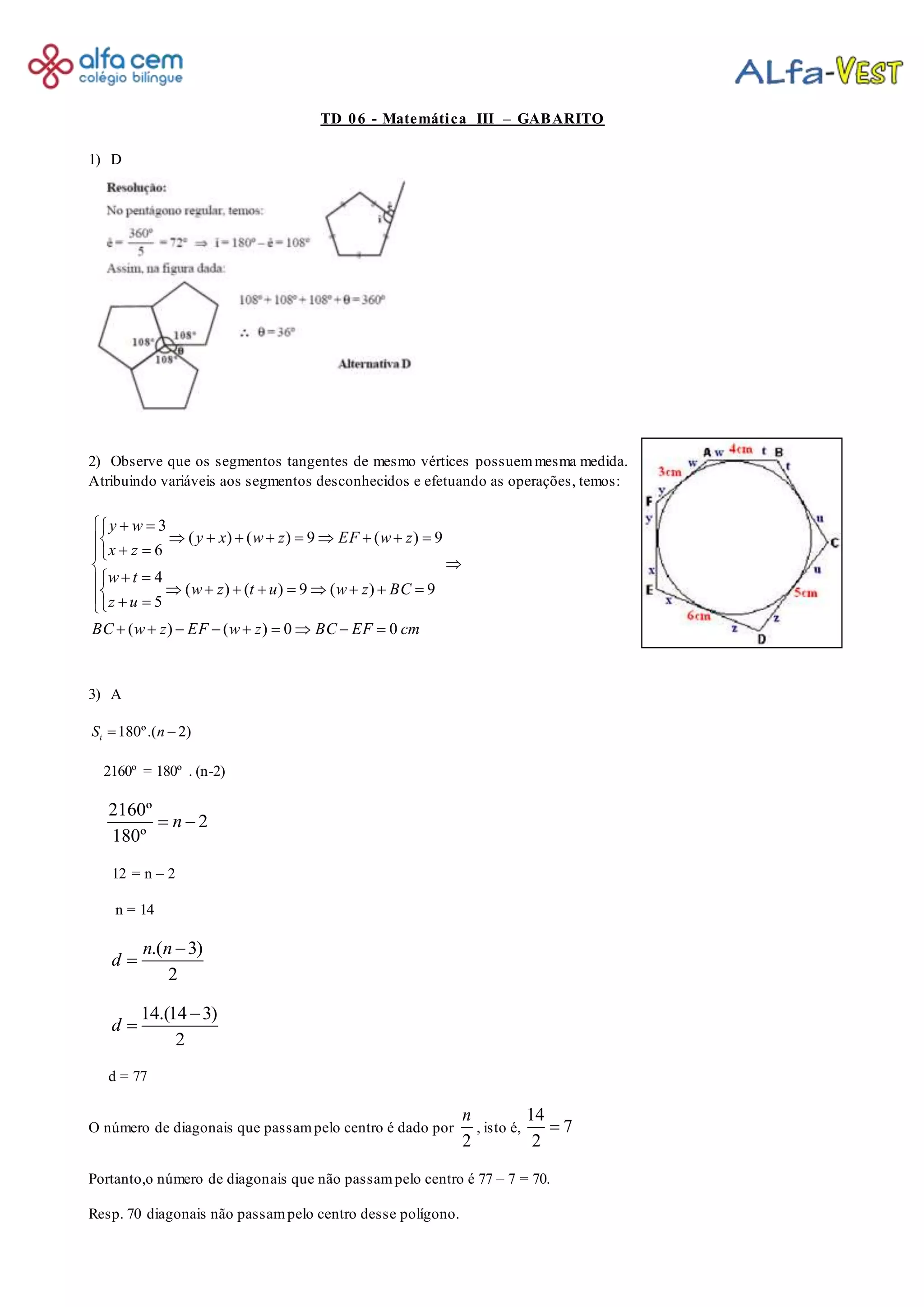
Este documento contém: 1) A resolução de uma questão de matemática envolvendo cálculos geométricos com segmentos e ângulos. 2) A explicação de que em um polígono regular com 14 lados, há 70 diagonais que não passam pelo centro. 3) A identificação de que o polígono com ângulo central de 30° é o dodecágono regular.

1. TD 06 - Matemática III – GABARITO
1) D
2) Observe que os segmentos tangentes de mesmo vértices possuemmesma medida.
Atribuindo variáveis aos segmentos desconhecidos e efetuando as operações, temos:
cmEFBCzwEFzwBC
BCzwutzw
uz
tw
zwEFzwxy
zx
wy
00)()(
9)(9)()(
5
4
9)(9)()(
6
3





















3) A
180º.( 2)iS n 
2160º = 180º . (n-2)
2160º
2
180º
n 
12 = n – 2
n = 14
.( 3)
2
n n
d


14.(14 3)
2
d


d = 77
O número de diagonais que passampelo centro é dado por
2
n
, isto é,
14
7
2

Portanto,o número de diagonais que não passampelo centro é 77 – 7 = 70.
Resp. 70 diagonais não passampelo centro desse polígono.

2. 4) A
5) C
6) Sim
7) B
8) 5 e 9

3. 9)
Analisando os ângulos centrais destacados, observamos que MOˆQ mede 90º, pois é
formado pelas metades das diagonais do quadrado MQRS e elas cortam-se ao meio
perpendicularmente. O arco MN mede 120º, pois é limitado por dois vértices do triângulo
equilátero inscrito. Logo, o ângulo central MOˆN mede 120º. O ângulo central x mede
120º - 90º = 30º. O segmento QN é lado do polígono regular que apresenta o ângulo
central de 30º. Temos: 12
º30
º360º360
 n
n
centralângulo . O polígono é o
dodecágono regular.
10) A
d =
𝑛.(𝑛−3)
2
d =
15.(15−3)
2
d =
15.12
2
d = 15. 6
d = 90
11) C
No pentágono regular, o ângulo interno é dado por:
180º(5 2) 180º.3 540º
108º
5 5 5
ia

   
Para encontrarmos o valor do ângulo a, fazemos:
108º + 108º + a = 360º
a = 360º - 108º - 108º
a = 144º
Como em todo losango os ângulos adjacentes são suplementares, temos:
a + b = 180º
144º + b = 180º
b = 180º - 144º
b = 36º
Por fim, fazemos
2
b
a  = 144º - 18º = 126º
Resp. A diferença é de 126º.
12) B
Logo, são 27 diagonais.

4. 13)