1. O documento descreve as propriedades de relações binárias, incluindo: produto cartesiano, domínio, imagem, relações reflexivas, simétricas, transitivas e anti-simétricas. 2. Uma relação de equivalência é uma relação que é reflexiva, simétrica e transitiva. As classes de equivalência formam uma partição do conjunto. 3. Exemplos mostram como verificar se uma relação é de equivalência e como determinar classes de equivalência.

1. RELAÇÕES
1. Produto cartesiano
Sejam A e B conjuntos não vazios. Chama-se produto cartesiano de A por B o
conjunto de todo os pares ordenados ( x, y ) com x ∈ A e y ∈ B .
Notação:
A × B = {( x, y ) | x ∈ A e y ∈ B}
2. Relação binária
Denomina-se relação binária de A em B a todo subconjunto ℜ de A × B . Se
( x, y ) ∈ℜ indicamos por xℜy e ( x, y ) ∉ℜ indicamos por x ℜy .
3. Domínio e imagem
Seja ℜ uma relação binária de A em B.
Denomina-se domínio de ℜ o subconjunto de A, dos elementos de x ∈ A para os quais
existe algum y em B com xℜy .
Denomina-se imagem de ℜ o subconjunto de B, dos elementos de y ∈ B para os quais
existe algum x em A com xℜy .
Im ℜ = { y ∈ B | ∃x ∈ A : xℜy}
4. Propriedades das relações
Seja ℜ ⊂ A × B.
i) Reflexiva
Dizemos que ℜ é reflexiva se ( ∀x ) ( x ∈ A → xℜx) ou ( ∀x ) ( x ∈ A → ( x, x) ∈ℜ)
Exemplo 1:
Mostremos que as relações dadas são reflexivas.
a) Seja ℜ = {( a, a ),(b, b),(c, c ),(a, c),(b, a )} sobre A = {a, b, c} .
ℜ é reflexiva, pois aℜa, bℜb e cℜc .
{
b) Seja ℜ = ( x, y ) ∈
2
| x = y}
ℜ é reflexiva, pois para ∀x ∈ , x = x
c) Seja ℜ = {( r , s ) ∈ S | rℜs ↔ r s} sendo S plano euclidiano.
2
ℜ é reflexiva, pois para ∀r ∈ S , r r
1

2. ii) Simétrica
Dizemos que ℜ é simétrica se, e somente se ( ∀x, y ∈ A) ( xℜy → yℜx) .
Exemplo 2:
Mostremos que as relações dadas são simétricas.
a) Seja ℜ = {( a, a ),(b, b),( a, b),(b, a )} sobre A = {a, b} .
ℜ é simétrica, pois aℜb → bℜa .
b) Seja ℜ a relação de perpendicularidade definida por:
{ }
ℜ = (r , s ) ∈ S 2 | rℜs ↔ r ⊥ s sendo S plano euclidiano.
ℜ é simétrica, pois rℜs → sℜr .
iii) Transitiva
Dizemos que ℜ é transitiva se, e somente se (∀x, y, z )(( xℜy e yℜz ) → xℜz ) .
Exemplo 3:
Mostremos que a relação ℜ = {( a, a ),( a, b),(b, c),( a, c )} sobre A = {a, b, c} é
transitiva.
ℜ é transitiva pois, (aℜb e bℜc) → aℜc .
iv) Anti-simétrica
Dizemos que ℜ é anti-simétrica se, e somente se ( ∀x, y ∈ A) (( xℜy e yℜx) → x = y ) ou
equivalente ( ∀x, y ∈ A) ( x ≠ y → ( x ℜy ou y ℜx)) .
Exemplo 4:
Mostremos que a relação ℜ = {( a, a ),(b, b),( a, b),( a, c)} sobre A = {a, b, c} é anti-
simétrica.
A sentença ( aℜb e bℜa ) → a = b é verdadeira, pois F → F é verdadeira.
Exemplo 5:
A relação ℜ = {( a, a ),(b, b),( a, b),(b, a ),(c, c)} sobre A = {a, b, c} não é anti-simétrica.
Não é anti-simétrica pois, a ≠ b → (aℜb e bℜa ) .
Observação:
Se A é um conjunto finito com poucos elementos, é possível visualizar as propriedades
por meio dos diagramas.
2

3. Reflexiva: Em cada ponto do diagrama Simétrica: Toda flecha deve ter duas pontas.
deve ter um laço.
a
b b
a
c c d
Transitiva: Todo par de flechas consecutivas Anti-simétrica: Não há flechas com
deve existir uma flecha cuja origem é a duas pontas.
primeira e extremidade é a segunda.
b b
a a
c d c d
5. Relação de equivalência
Uma relação ℜ sobre A não vazio denomina-se relação de equivalência sobre A se, e
somente se, ℜ for reflexiva, simétrica e transitiva.
Exemplo 6:
A relação ℜ = {( a, a ),(b, b),(c, c ),(c, a ),( a, c)} sobre A = {a, b, c} é de equivalência
pois, valem as três propriedades: reflexiva, simétrica e transitiva.
Exemplo 7:
Seja A = . A relação ℜ definida por xℜy ↔ x = y, ∀x, y ∈ é de equivalência.
i )Reflexiva
A relação ℜ é reflexiva pois, (∀x)( x ∈ → x = x)
ii)Simétrica
A relação ℜ é simétrica pois, (∀x, y ∈ )( x = y → y = x)
3

4. iii) Transitiva
A relação ℜ é transitiva pois, (∀x, y, z ∈ )( x = y e y = z ) → x = z )
Exemplo 8:
A relação de paralelismo no plano euclidiano S é uma relação de equivalência. Assim
(∀r , s ∈ S )(rℜs ↔ r s )
i )Reflexiva
A relação ℜ é reflexiva pois, (∀r )(r ∈ S → r r )
ii)Simétrica
A relação ℜ é simétrica pois, (∀r , s ∈ S )( r s → s r )
iii) Transitiva
A relação ℜ é transitiva pois, (∀r , s, t ∈ S )(r s e s t ) → r t ) .
Exercícios de Aplicação 1:
Diga quais propriedades são válidas para as relações definidas a seguir.
1) ℜ = {( a, a ),(b, b),(c, c),(c, a )} sobre iii) Transitiva
A = {a, b, c}
i )Reflexiva
iv) Anti-simétrica
ii)Simétrica
2) ℜ = {( a, a ),( a, b)} sobre A = {a, b} iii) Transitiva
i )Reflexiva
ii)Simétrica
iv) Anti-simétrica
4

5. 3) ℜ = {(a, a ),(b, b),(b, a )} sobre A = {a, b} iii) Transitiva
i )Reflexiva
iv) Anti-simétrica
ii)Simétrica
4) ℜ = {( a, a ),(b, b),(c, c ),(a, b),(b, a )} iii) Transitiva
sobre A = {a, b, c}
i )Reflexiva
iv) Anti-simétrica
ii)Simétrica
{
5) Seja ℜ = ( x, y ) ∈
2
| x 2 + y 2 = 1} , iii) Transitiva
quais propriedades são válidas para as
relação.
i )Reflexiva
iv) Anti-simétrica
ii)Simétrica
6. Classe de equivalência
Seja ℜ uma relação de equivalência sobre A.
Dado a ∈ A, denomina-se classe de equivalência determinada por a, o subconjunto de A
formado dos elementos x tal que xℜa. Simbolicamente
a = { x ∈ A | xℜa}
5

6. 7. Conjunto quociente
O conjunto das classes de equivalência denomina-se conjunto quociente e se indica por A / ℜ
Exemplo 9:
A relação ℜ = {( a, a ),(b, b),(c, c ),(c, a ),( a, c)} sobre A = {a, b, c} é de
equivalência.Determinemos suas classes de equivalência começando por a, assim:
a = {a, c} ,pois, aℜa e aℜc e cℜa
b = {b} , pois, bℜb
c = {c, a} , pois, cℜc e aℜc e cℜa , logo podemos ver que a classe a = c , assim
temos duas classes, e indicamos por:
A / ℜ = {a , b } = {{a, c} , b}
Exemplo 10:
Seja a relação de equivalência ℜ sobre A = {a, b, c, d , e, f }
ℜ = {(a, a),(b, b),(a, b),(b, a),(c, c),(d , d ),(d , e),(e, d ),(e, e),(e, f ),( f , e),( f , f ),( f , d ),(d , f )}
Determinemos suas classes de equivalência.
a = {a, b} , pois, aℜa e aℜb e bℜa
c = {c} pois, cℜc
d = {d , e, f } pois, d ℜd e d ℜf e d ℜe,...
e escrevemos o conjunto quociente:
A / ℜ = {{a, b} ,{c}{d , e, f }}
8. Partição de um conjunto
Seja A um conjunto não vazio. Diz-se que a classe dos subconjuntos de A é uma partição
de A se, e somente se
1) (∀r )( Br ≠ φ )
2) Se r ≠ s → Br ∩ Bs = φ ou Br = Bs
n
3) UB r
=A
r =1
Exemplo 11:
Utilizando o exemplo 10 podemos escrever que A = {a, b, c, d , e, f }
e A/ℜ = {{a, b} ,{c}{d , e, f }} , assim A / ℜ forma uma partição de A pois. Denominando
6

7. B1 = {a, b}
B2 = {c}
3
B3 = {d , e, f } , tem-se UB r
= A e a intersecção de dois a dois é sempre vazia e
r =1
(∀r )( Br ≠ φ )
Exemplo 12:
Sejam A = × e ℜ definida por ( a, b)ℜ(c, d ) ↔ a + d = b + c .
a) Verifique se ℜ é uma relação de equivalência.
b) Caso afirmativo dar a classe de (2,3) .
Deixamos a cargo do leitor a demonstração
i )Reflexiva
ii)Simétrica
iii) Transitiva
a) ( a, b)ℜ(c, d ) ↔ a + d = b + c
(c, d )ℜ(e, f ) ↔ c + f = d + e , adicionando membro a membro e simplificando tem-se;
(a + f = b + e) → (a, b)ℜ(e, f ) , logo ℜ é transitiva e portanto é uma relação de
equivalência.
b) Classe de (2,3) = {( x, y ) ∈ × | ( x, y )ℜ(2,3)} = {( x, y ) ∈ × | x + 3 = y + 2} =
{(2,3),(1, 2),(3, 4),....}
Exercícios de aplicação 02:
1)Sejam A = × e ℜ definida por iii) Transitiva
*
(a, b)ℜ(c, d ) ↔ ad = bc .
a) Verifique se ℜ é uma relação de
equivalência
i )Reflexiva
b) Caso afirmativo, dar a classe de (2,3) .
ii)Simétrica
7

8. 2) Seja a relação de equivalência ℜ sobre iii) Transitiva
definida por nℜm ↔ i = i , i = −1
n m
a) Verifique se ℜ é uma relação de
equivalência b) Caso afirmativo dar /ℜ.
i )Reflexiva
ii)Simétrica
3) Seja iii) Transitiva
f: *
→ ,definida por f ( x) = 1 + x . 2
a) Mostre que
ℜ = {(a, b) ∈ *
× | af (b) = bf (a)} é de
equivalência.
i )Reflexiva b) Caso afirmativo dar a classe 3 .
ii)Simétrica
4)Sejam A = e ℜ definida por iii) Transitiva
(a, b) ∈ℜ ↔ 3/ a − b .(lê-se 3 divide a-b)
a) Verifique se ℜ é uma relação de
equivalência.
i )Reflexiva
b) Caso afirmativo, dar /ℜ
ii)Simétrica
8

9. 5) Seja A = {a, b, c, d } , complete o quadro
Relação ℜ Reflexiva Simétrica transitiva
ℜ = {(a, a),(b, b),(c, c),(d , d )}
ℜ = {(a, c),(c, a),(c, c ),(a, d )}
ℜ = {(a, a),(b, b),(a, b),(b, a),(b, d ),(d , b)}
6) Seja a relação de equivalência ℜ sobre
(conjunto dos números complexos)definida
por
( x + yi) ℜ( z + ti) ↔ x + y = z + t , i = −1
Descreva geometricamente a classe de
equivalência determinada por 2 + 3i
7) Seja f : → ,e a iii) Transitiva
relação ℜ = {(a, b) ∈ * × | af (b) = bf (a)}
a) Mostre que é de equivalência.
i )Reflexiva
b)Sendo f ( x ) = x , dar a classe 2 .
2
ii)Simétrica
8) Em
∗
× , definimos a relação ℜ de
∗
equivalência por
( x, y )ℜ(a, b) ↔ ∃k ∈ | x = ka e y = kb
∗
Descreva geometricamente
∗
× ∗
ℜ
9

10. 9. Relação de ordem
Seja A um conjunto não vazio. Diz-se que a relação ℜ é de ordem parcial sobre A se, e
somente se, ℜ for reflexiva, anti-simétrica e transitiva, isto é, são verdadeiras as propriedades:
i) ℜ é reflexiva se ( ∀x ) ( x ∈ A → xℜx)
ii) ℜ é anti-simétrica se, e somente se ( ∀x, y ∈ A) (( xℜy e yℜx) → x = y )
iii) ℜ é transitiva se, e somente se (∀x, y , z )(( xℜy e yℜz ) → xℜy ) .
Notação: Se aℜb e é uma relação de ordem parcial escrevemos a p b , lê-se “ a precede b” ou
“ a antecede b”
Se a relação ℜ é de ordem parcial sobre A, então dizemos que A é parcialmente
ordenado.
Elementos comparáveis
Se a relação ℜ é de ordem parcial sobre A. Os elementos a e b de A, se dizem
comparáveis se a p b ou b p a .
10. Ordem total
Se a relação ℜ é de ordem parcial sobre A e os elementos a e b de A, forem comparáveis
isto é, a p b ou b p a , então ℜ é de ordem total. Nesse caso o conjunto A se diz totalmente
ordenado.
Exemplo 13:
Sejam A = e a relação ℜ definida por xℜy ↔ x ≤ y (menor ou igual é uma relação
de ordem total, denominada ordem habitual).
Mostremos que ≤ é uma relação de ordem total.
i) ℜ é reflexiva, pois ( ∀x ) ( x ∈ → x ≤ x)
ii) ℜ é anti-simétrica, pois ( ∀x, y ∈ ) (( x ≤ y e y ≤ x) → x = y)
iii) ℜ é transitiva, pois (∀x, y , z ∈ )(( x ≤ y e y ≤ z ) → x ≤ z ) . Portanto ℜ é de ordem
parcial sobre .
Verifiquemos se é de ordem total;
( ∀x, y ∈ ) (se x, y ∈ → x ≤ y ou y ≤ x) ,logo ℜ é de ordem total.
11. Limites superiores e inferiores
Seja A um conjunto parcialmente ordenado mediante a relação p . Seja B ≠ φ um
subconjunto de A .
Chamamos de limite superior de B a todo elemento L ∈ A | x p L, ∀x ∈ B
Chamamos de limites inferior de B a todo elemento l ∈ A | l p x, ∀x ∈ B
10

11. 12. Máximo e Mínimo
Sejam B ⊂ A e p uma relação de ordem parcial.
Se L ∈ B, então L é máximo.
Se l ∈ B, então l é mínimo.
13. Supremo e Ínfimo
Seja A um conjunto parcialmente ordenado mediante a relação p . Seja B ≠ φ um
subconjunto de A .
Chama-se supremo de B o mínimo do conjunto dos limites superiores de B (caso exista)
Chama-se ínfimo de B o máximo do conjunto dos limites superiores de B (caso exista).
11. Boa ordem
ℜ é boa ordem sobre A se, qualquer subconjunto de A possuir mínimo
Exemplo 12:
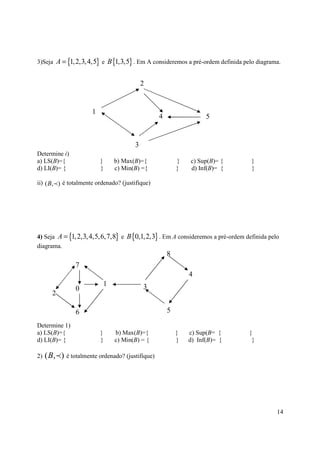
Sejam , A =] − 1, 2] e ℜ a ordem habitual. Determinar
a) Limites superiores de A, LS(A)= { L ∈ | L ≥ 2}
b) Máximo de A, Max(A)= {2}
c) Supremo de A, Sup(A)= {2}
d) Limites inferiores de A, LI(A)= {l ∈ | l ≤ −1}
e) Mínimo de A, não existe Min(A)
f) Ínfimo de A, Inf(A)= {−1}
Exemplo 14:
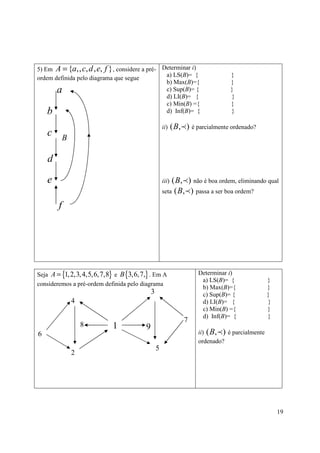
Sejam A = {a, b, c, d , e} e o diagrama simplificado da pré-ordem. Determinar os
conjuntos indicados. ( no diagrama vê-se que a > c )
a
c e
b
d
a) Max(A)= {a} b) Sup(A)= {a}
c) Min(A) = não existe d) Inf(A) = não existe
11

12. Exemplo 15:
Seja A = {1, 2,3, 4,5,6,7,8} e B {3,6,7,} . Em A consideremos a pré-ordem definida pelo
diagrama.
8
7
4
1
2 3
6 5
Determinar i)
a) LS(B)={7} b) Max(B)={7} c) Sup(B)= {7}
d) LI(B)={3,4,5,8 } c) Min(B) ={3} d) Inf(B)= {3,4,5,8}
ii) B é parcialmente ordenado (justifique)
a) Reflexiva vale, pois, é pré-ordenado.
b) Transitiva: Todo par de flechas consecutivas tem uma flecha cuja origem é a primeira e
extremidade é a segunda.
c) Anti-simétrica: Devemos verificar se vale a propriedade para o conjunto B.
(3 p 7 ∧ 7 p 3) → 3 = 7, F → F é verdadeira. Analogamente para 3 e 6 e 6 e 7.
iii) B é totalmente ordenado (justifique)
Como B é pré-ordenado, devemos verificar se todos os elementos de B são comparáveis.
3 p 7 ou 7 p 3 (V)
3 p 6 ou 6 p 3 (V)
6 p 7 ou 7 p 6 (V), logo , é totalmente ordenado.
12

13. Exercícios de aplicação 03:
1) Seja A = {1, 2,3, 4,5,6,7,8,9,10} e B {2,3,5} . Em A consideremos a pré-ordem definida
pelo diagrama.
1
2 10
6
4
3
9
8
5
7
Determinar i)
a) LS(B)={ } b) Max(B)={ } c) Sup(B)= { }
d) LI(B)={ } c) Min(B) ={ } d) Inf(B)= { }
ii) ( B, p ) é totalmente ordenado?
2)Seja A = {1, 2,3,4,5,6,7} e B {4,5,7} . Em A consideremos a pré-ordem definida pelo
diagrama.
7
4 5 6
1 2 3
Determine i)
a) LS(B)={ } b) Max(B)={ } c) Sup(B= { }
d) LI(B)= { } e) Min(B) ={ } f) Inf(B)= { }
ii) ( B, p ) é totalmente ordenado? (justifique)
iii) O que se deve fazer para ser ( B, p ) parcialmente ordenado
iv) ( B, p ) é bem ordenado se todos seus subconjuntos têm mínimo. Verifique se B é bem
ordenado
13

14. 3)Seja A = {1, 2,3, 4,5} e B {1,3,5} . Em A consideremos a pré-ordem definida pelo diagrama.
2
1
4 5
3
Determine i)
a) LS(B)={ } b) Max(B)={ } c) Sup(B)= { }
d) LI(B)= { } c) Min(B) ={ } d) Inf(B)= { }
ii) ( B, p ) é totalmente ordenado? (justifique)
4) Seja A = {1, 2,3,4,5,6,7,8} e B {0,1, 2,3} . Em A consideremos a pré-ordem definida pelo
diagrama.
8
7
4
1 3
0
2
6 5
Determine 1)
a) LS(B)={ } b) Max(B)={ } c) Sup(B= { }
d) LI(B)= { } c) Min(B) = { } d) Inf(B)= { }
2) ( B, p ) é totalmente ordenado? (justifique)
14

15. Exercícios de aplicação 04:
1) Seja ℜ = {( x, y ) ∈ | x( x − 1) = y ( y − 1)} . b) Verifique se ℜ é anti-simétrica.
a) Determinar x ∈ − {1} , tal que xℜ2.
2) Seja f : → , e a relação ℜ dada por iii) Transitiva
ℜ = {(a, b) ∈ × | f (a) − f (b) = a − b}
a) Verifique se ℜ é uma relação de
equivalência
i )Reflexiva
b) Sendo f ( x) = x 2 + 1 , determinar 3.
ii)Simétrica
3) Em × , definimos a relação ℜ de por iii) Transitiva
( x, y )ℜ( x1 , y1 ) ↔ y − y1 = 2( x − x1 )
a) Verifique se ℜ é de equivalência
i )Reflexiva
b) Descreva geometricamente ×
ii)Simétrica ℜ
15

16. 4) Em × , definimos a relação ℜ de por b) Determine (k , 0) , k ∈ .
( x, y )ℜ( x1 , y1 ) ↔ y1 − y = ( x1 − x)
a) Verifique se ℜ é de equivalência
i )Reflexiva
c) Descreva geometricamente ×
ii)Simétrica ℜ
iii) Transitiva
5) Sejam A = × * e ℜ relação de equivalência definida por
(a, b)ℜ(c, d ) ↔ a − b 2 = c − d 2 .
Determine os valores de k , para que (2, k ) ∈ (k − 1,3)
16

17. Exercícios de aplicação 04:
1) Seja A = {1, 2,3, 4,5,6} e B {2,3, 4} . Em Determinar i)
a) LS(B)= { }
A consideremos a pré-ordem definida pelo
b) Max(B)={ }
diagrama.
c) Sup(B)= { }
1 4 B d) LI(B)= { }
c) Min(B) ={ }
d) Inf(B)= { }
3 ii) ( B, p ) é parcialmente ordenado?
5
2 6
iii) ( B, p ) é totalmente ordenado?
Determinar i)
2) Seja A = {1, 2,3, 4,5,6} e B {2, 4,5} . Em a) LS(B)= { }
b) Max(B)={ }
A consideremos a pré-ordem definida pelo
c) Sup(B)= { }
diagrama.
d) LI(B)= { }
5 c) Min(B) ={ }
B d) Inf(B)= { }
2 6 ii) ( B, p ) é parcialmente ordenado?
iii) ( B, p ) é totalmente ordenado?
1 4 3
17

18. 3) Seja A = {1, 2,3,4,5,6,7,8} e Determinar i)
a) LS(B)= { }
B {2,3,5,8} . Em A consideremos a pré- b) Max(B)={ }
ordem definida pelo diagrama. c) Sup(B)= { }
d) LI(B)= { }
8 2 B c) Min(B) ={ }
d) Inf(B)= { }
7 5 ii) ( B, p ) é parcialmente ordenado?
3
6 4 1
iii) ( B, p ) é totalmente ordenado
4) Seja A = {1, 2,3, 4,5,6} e B {1,5,6} . Em Determinar i)
a) LS(B)= { }
A consideremos a pré-ordem definida pelo
b) Max(B)={ }
diagrama.
c) Sup(B)= { }
d) LI(B)= { }
B c) Min(B) ={ }
4 6 d) Inf(B)= { }
5
ii) ( B, p ) é parcialmente ordenado?
1 2 3
18

19. 5) Em A = {a,, c, d , e, f } , considere a pré- Determinar i)
a) LS(B)= { }
ordem definida pelo diagrama que segue
b) Max(B)={ }
a c) Sup(B)= { }
d) LI(B)= { }
c) Min(B) ={ }
b d) Inf(B)= { }
ii) ( B, p ) é parcialmente ordenado?
c B
d
e iii)( B, p ) não é boa ordem, eliminando qual
seta ( B, p ) passa a ser boa ordem?
f
Seja A = {1, 2,3, 4,5,6,7,8} e B {3,6,7,} . Em A Determinar i)
a) LS(B)= { }
consideremos a pré-ordem definida pelo diagrama
b) Max(B)={ }
3 c) Sup(B)= { }
4 d) LI(B)= { }
c) Min(B) ={ }
d) Inf(B)= { }
7
8 1 9
6 ii) ( B, p ) é parcialmente
ordenado?
5
2
19

20. 20