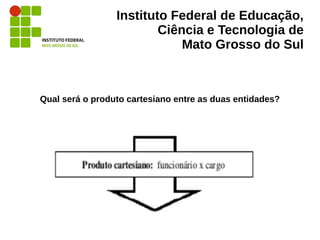
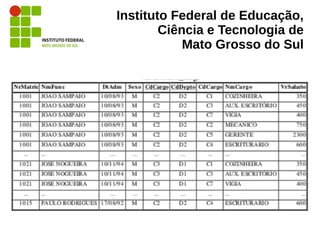
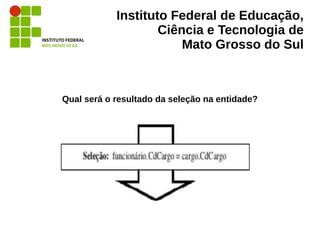
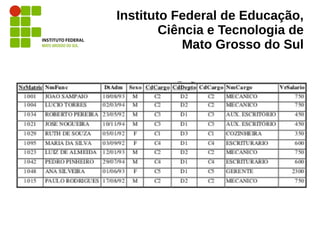
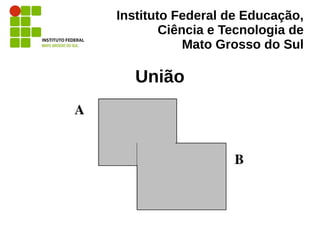
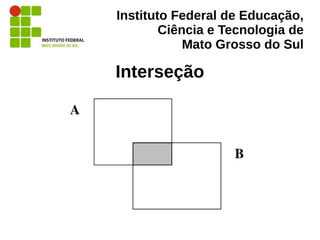
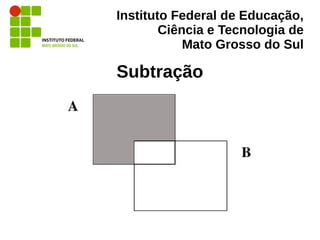
O documento aborda a álgebra relacional, fundamental para o estudo e a operação de bancos de dados relacionais, e exemplifica operações como seleção, projeção, união, interseção e produtos cartesianos. É descrito seu papel na implementação e otimização de consultas em sistemas de gerenciamento de banco de dados, além de fornecer definições e exemplos práticos em SQL. Referências de autores reconhecidos na área, como Elmasri e Navathe, são citadas ao longo do texto para suportar as definições apresentadas.

1. CURSO SUPERIOR DE TECNOLOGIA EM
ANÁLISE E DESENVOLVIMENTO DE
SISTEMAS – TADS
Projeto de Banco de Dados
Luiz Picolo
luizpicolo@luizpicolo.com.br

2. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Álgebra Relacional

3. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Definições
A álgebra é uma das vertentes da matemática
que estuda as estruturas e as relações. Por meio
deste estudo são criadas leis gerais, as quais,
possibilitando o desenvolvimento de equações e
análises correspondentes à sua resolução.

4. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Definições
Segundo Elmasri e Navathe (2011), com o
conjunto básico de operações para o modelo
relacional os quais permitem que um usuário
especifique as solicitações de recuperação básica
como expressões da álgebra relacional.

5. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
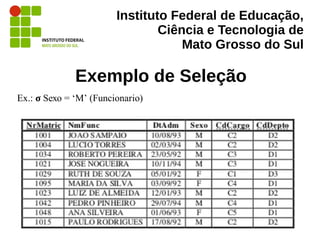
A importância da álgebra relacional
“ela oferece um alicerce formal para as
operações do modelo relacional” (Elmasri;
Navathe, 2011, p. 96)
“ela é usada como base para a implementação e
otimização de consultas nos módulos de […] de
processamento […] que são partes integrais dos
sistemas de gerenciamento de banco de dados
relacionais” (Elmasri; Navathe, 2011, p. 96)

6. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
A importância da álgebra relacional
“alguns de seus conceitos são incorporados na
linguagem de consulta SQL” (Elmasri; Navathe,
2011, p. 96), mas grande maioria dos conceitos
da linguagem de consulta são vindouros do
Calculo relacional de tupla.

7. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
As operações da álgebra relacional, aplicáveis
no modelo relacional, podem ser dividias em
duas partes.
● A primeira inclui um conjunto de operações da
teoria dos conjuntos
● A segundo grupo são operações desenvolvidos
especialmente para banco de dados relacionais

8. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
A primeira inclui as operações:
● União;
● Interseção;
● Diferenciação;
● Produto cartesiano.

9. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
A segunda inclui as operações:
● Seleção;
● Projeção;
● Junção.

10. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Demostração de Operações
básicas de álgebra Relacional

11. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Funcionario (NrMatric, NmFunc, DtAdm, Sexo, CdCargo, CdDepto)
Cargo (CdCargo, NmCargo, VrSalario)
Departamento (CdDepto, NmDepto, Ramal)

12. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Para a demostração as tabelas
foram populadas com o seguinte
conteúdo.

13. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Tabela Cargo

14. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Tabela Departamento

15. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Tabela Departamento

16. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Eric Grimsom & John Guttag - MIT
Use nomes, atributos e variáveis com sentido,
pois elas serão úteis quando você não se lembrar
mais delas.

17. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Operações Relacionais Unárias
Seleção e Projeção

18. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Definição de Seleção
Segundo Elmasri e Navathe (2011) a operação
de seleção é utilizada para escolher um
subconjunto das tuplas de uma relação que
satisfaça uma condição de seleção.

19. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Definição de Seleção
Em geral a operação de seleção e indicada pelo
simbolo Sigma, logo após vem a sua condição, e
por fim a relação ou entidade, a qual será
aplicada a seleção
Ex.: σ <condição de seleção> (R)

20. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Retorno de uma Seleção
A estrutura retornada é a mesma, porém, apenas
o conjunto de elementos, ou tuplas, que satisfaz a
condição farão parte do subconjunto
remanescente.

21. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Exemplo de Seleção
Ex.: σ Sexo = ‘M’ (Funcionario)

22. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Retorno da Seleção
Ex.: σ Sexo = ‘M’ (Funcionario)

23. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Mesmo sendo um modelo conceitual, pode-se aplicar a mesma
ideia na prática utilizando códigos SQLs. Em código SQL está
pesquisa seria:
SELECT * FROM Funcionario WHERE Sexo = 'M'

24. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Definição de Projeção
Já a operação de projeção será necessário
projetar a relação apenas nos atributos
desejados. Ao contrário da operação de seleção,
a projeção descarta algumas colunas enquanto
seleciona outras. π é o simbolo utilizado para
representar a projeção.

25. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Exemplo de Projeção
Ex.: π NmFunc, DtAdm (σ Sexo = ‘F’ (Funcionario))

26. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Retorno da Seleção
Ex.: σ Sexo = ‘F’ (Funcionario)

27. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Retorno da Projeção sobre a
Seleção
Ex.: π NmFunc, DtAdm (σ Sexo = ‘F’ (Funcionario))

28. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
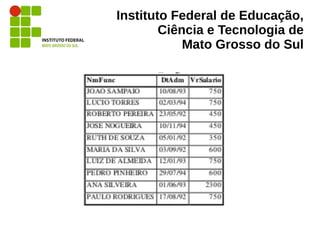
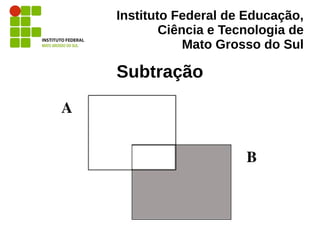
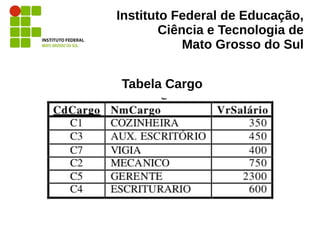
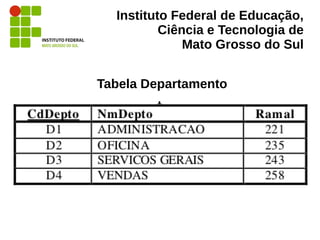
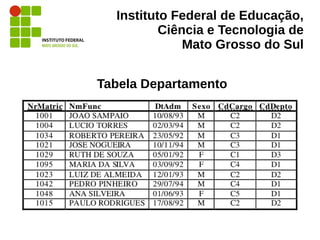
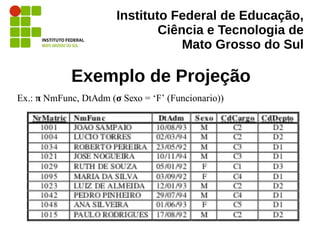
“Como a projeção não permite descartar linhas,
apenas colunas, deve-se fornecer a essa
operação o subconjunto resultante de uma
filtragem (seleção) da relação de funcionários
original, como mostram as duas figuras […], que
representam as relações e as operações de duas
maneiras diferentes.” (MUNARI. 2008)

29. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
A mesma pesquisa em SQL seria:
SELECT DISTINCT NumFunc, DtAdm FROM
Funcionario WHERE Sexo = 'F'

30. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Produto Cartesiano

31. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Produto Cartesiano
O resultado do produto cartesiano entre duas
tabelas é uma terceira tabela a qual conterá todas
as relações possíveis entre os elementos
contidos nas tabelas originais.

32. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Produto Cartesiano
Ex.: π NmFunc, DtAdm, VrSalário (σ funcionário.CdCargo =
cargo.CdCargo (funcionário x cargo))

33. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Qual será o produto cartesiano entre as duas entidades?

34. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul

35. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Qual será o resultado da seleção na entidade?

36. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul

37. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Qual será o resultado da projeção na entidade?

38. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul

39. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Operações de álgebra relacional
com base na teoria dos
conjuntos.
União, Interseção e Subtração.

40. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
União
Segundo Elmasri e Navathe (2011), o resultado
da operação União, a qual é indicado pelo
simbolico A B∪ , é uma relação que inclui todas
as tuplas que estão em A ou em B ou tanto em A
quando em B.

41. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
União

42. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
União em SQL
Em SQL: SELECT * FROM A UNION SELECT * FROM B

43. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Interseção
Já a interseção, A ∩ B , inclui todas as tuplas que
estão em A e em B. Esta é uma operação
adicional que produz como resultado uma tabela
que contém, sem repetições, todos os elementos
que são comuns às duas tabelas fornecidas.

44. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Interseção

45. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Interseção em SQL
Em SQL: SELECT * FROM A INNER JOIN B ON (A = B)

46. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Subtração
Já a subtração ou diferenciação de conjuntos, diz
respeito a uma relação A – B , que inclui todas as
tuplas que estão em A mas não em B.

47. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Subtração

48. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Subtração

49. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Interseção em SQL
Em SQL: SELECT * FROM A INNER JOIN B ON (A != B)
ou SELECT * FROM B INNER JOIN B ON (B != A)

50. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Operações relacionais binárias.
Junção e Divisão.
Em operação de junção o produto é a
combinação entre as linhas de uma tabela com
as linhas correspondentes de outra tabela, sendo
em princípio correspondente a uma seleção pelos
atributos de relacionamento sobre um produto
cartesiano dessas tabelas.
Ex.: A |x| B = σ A.chave1 = B.chave2 (A x B)

51. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Operações relacionais binárias.
Junção e Divisão.
A tabela resultante de uma junção tem todas as
colunas da primeira tabela e todas da segunda
tabela. Isso faz com que os valores dos campos
utilizados como critério para a correspondência
entre as linhas apareça duplicado, já que um vem
da primeira tabela e outro da segunda.

52. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Operações relacionais binárias.
Junção e Divisão.
Um operação adicional que produz como
resultado a projeção de todos os elementos da
primeira tabela que se relacionam com todos os
elementos da segunda tabela. Queremos saber
os nomes dos departamentos que possuem todos
os cargos.
Ex.: π NmDepto, CdCargo ( depto |x| funcionário ) ÷ π CdCargo ( cargo )

53. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Atribuição: variável ← A
Permite que o conteúdo de uma tabela seja
atribuído em uma variável especial, oferecendo a
possibilidade de um tratamento até certo ponto
algorítmico para algumas sequências de
operações.

54. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul

55. Instituto Federal de Educação,
Ciência e Tecnologia de
Mato Grosso do Sul
Referências Bibliográficas
ELMASRI, RAMEZ; NAVATHE, SHAMKANT B. Sistema de banco de
dados. Tradução Daniel Vieira; revisão técnica Enzo Seraphim e
Thatyane de Faria Piola Seraphim. – 6. ed. – São Paulo: Person
Addison Wesley. 2011
MUNARI, A. C. B. Operações relacionais e Álgebra relacional.
Acesso em: 31 de Maio de 2013. Disponível em:
http://www.pucrs.campus2.br/~jiani/bd/OpRelacional.pdf.