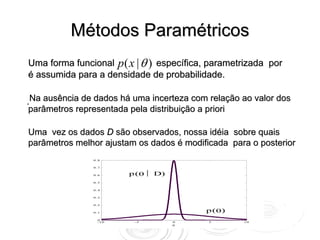
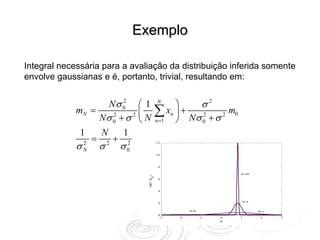
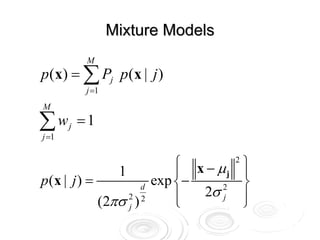
O documento discute métodos para estimar densidades de probabilidade a partir de dados, incluindo métodos paramétricos bayesianos, métodos de núcleo e misturas de distribuições. O algoritmo EM é descrito como uma abordagem para inferir parâmetros de misturas de distribuições maximizando a verossimilhança dos dados.

1. Estimação
de Densidades
Renato Vicente
rvicente@if.usp.br
10/01, mpmmf, IME/FEA – USP

2. Estimação de Densidades
Métodos Paramétricos
Métodos de Núcleo (Kernel Methods)
Misturas de Distribuições
Algoritmo EM

3. Métodos Paramétricos
Uma forma funcional p ( x | θ ) específica, parametrizada por θ
é assumida para a densidade de probabilidade.
.Na ausência de dados há uma incerteza com relação ao valor dos
parâmetros representada pela distribuição a priori p (θ )
Uma vez os dados D são observados, nossa idéia sobre quais
parâmetros melhor ajustam os dados é modificada para o posterior
p (θ | D) 0 .8
0 .7
0 .6 p(θ⏐ D)
0 .5
0 .4
0 .3
0 .2
0 .1
p(θ)
0
-1 0 -5 0 5 10
θ

4. Métodos Paramétricos
A densidade que se deseja inferir a partir dos dados D é
p( x | D)
Considerando a parametrização
p ( x | D) = ∫ p ( x,θ | D) dθ
= ∫ p ( x | θ , D) p (θ | D) dθ
=∫ p( x | θ ) p (θ | D) dθ
densidade assumida posterior =
a priori atualizado

5. Métodos Paramétricos
O posterior pode ser obtido do a priori via Teorema de
Bayes:
p( D | θ )
p (θ | D) = p (θ )
∫ p( D | θ ′) p(θ ′) dθ ′
Assumindo independência entre cada uma das amostras
do conjunto de dados D a verossimilhança pode ser
fatorada: N
p ( D | θ ) = ∏ p ( xn | θ )
n =1

6. Métodos Paramétricos
θ
O a priori p ( ) pode ser escolhido utilizando critérios
de tratabilidade das integrais ou critérios informacionais.
Se o a priori e o posterior estiverem na mesma família o
a priori é dito conjugado.
A densidade
p (θ | D) pode ser utilizada como novo a
priori e atualizada com um novo dado xN+1 segundo:
p ( D, xN +1 | θ )
p (θ | D, xN +1 ) = p (θ | D)
∫ p( D, xN +1 | θ ′) p(θ ′ | D) dθ ′

7. Exemplo: Estimação Bayesiana em 1D
Suponhamos um conjunto de dados D = {x1 , , xN }
Assumimos que os dados são gerados de forma independente
com distribuição gaussiana com desvio padrão σ
conhecido.
Queremos inferir a média m.
Assim p ( x D ) = ∫ p ( x | m) p (m | D ) dm
1
1 − ( x − m )2
p ( x m) = 2σ 2
Onde assumimos que e
2πσ 2

8. Exemplo
Assumimos a seguinte estrutura para a densidade a priori:
1
− ( m − m0 ) 2
1 2σ 0
p ( m) =
2
e
2πσ 2
0
A densidade posterior para o parâmetro m após a
apresentação dos dados é N
∏ p( x n | m)
p(m | D) = n =1
N
p ( m)
∫ p(m′)∏ p( x
n =1
n | m′) dm′

9. Exemplo
Integral necessária para a avaliação da distribuição inferida somente
envolve gaussianas e é, portanto, trivial, resultando em:
Nσ 0 ⎛ 1
2 N
⎞ σ2
mN =
Nσ 0 + σ 2 ⎜ N
2
⎝
∑ xn ⎟ + Nσ 2 + σ 2 m0
n =1 ⎠ 0
1 N 1
= +
σN
2
σ2 σ0
2 12
10
8
) N=50
N
D 6
⏐
m
(
P
4
2 N=5
N=0 N=1
0
-3 -2 -1 0 1 2 3
m

10. Métodos de Kernel
A probabilidade de que um vetor x, amostrado de uma
densidade p(x) desconhecida, caia em uma região R do
espaço dos vetores é
P = ∫ p (x′) d x′
R
A probabilidade de que em N amostras, K estejam em R é
⎛N⎞ K
PN ( K ) = ⎜ ⎟ P (1 − P ) N − K
⎝K⎠
⎡K ⎤
P= E⎢ ⎥
Um estimador para a probabilidade de R é ⎣N ⎦

11. Métodos de Kernel
A variância em torno deste estimador é
⎡⎛ K ⎞ ⎤ P(1 − P)
2
E ⎢⎜ − P ⎟ ⎥ = ⎯⎯⎯ 0
N →∞
→
⎢⎝ N
⎣ ⎠ ⎥⎦ N
K
Assim P
N P = ∫ p (x′) dx′ p (x)V
R
Mas
P K
p ( x) =
V NV

12. Janela de Parzen
⎧ 1
⎪1 se u j < , j = 1,..., d
H (u) = ⎨ 2 X
⎪
⎩ 0, c.c.
h
N
⎛x−x ⎞ n
K = ∑H ⎜ ⎟
n =1 ⎝ h ⎠
K 1 1 ⎛ x − xn ⎞
N
p ( x) = = ∑ d H⎜ ⎟
NV N n =1 h ⎝ h ⎠

13. Mixture Models
M
p (x) = ∑ Pj p (x | j )
j =1
M
∑w
j =1
j =1
⎧ x−μ 2
⎫
1 ⎪ ⎪
p(x | j ) = exp ⎨−
j
⎬
d
⎪ 2σ j
2
⎪
(2πσ j )
2 2
⎩ ⎭

14. Mixture Models
Os parâmetros μ j e σ j podem ser inferidos
minimizando uma função erro (maximizando a
verossimilhança)
N
E ( μ j , σ j ) = −∑ ln p(x n )
n =1
N M
= −∑ ln ∑ Pj p (x n | j )
n =1 j =1

15. Algoritmo EM
A variação da função erro pode ser escrita :
⎛ P ′( x n ) ⎞
ΔE = − ∑ ln ⎜
⎜ P (x ) ⎟ ⎟
n ⎝ n ⎠
⎛ Pj′ P ′( x n | j ) P ( j | x n ) ⎞
= − ∑ ln ⎜ ∑
⎜ j ⎟
n ⎝ P ( xn ) P( j | xn ) ⎟ ⎠
Utilizando a desigualdade de Jensen
⎛ ⎞
ln ⎜ ∑ λ j x j ⎟ ≥ ∑ λ j ln( x j )
⎝ j ⎠ j

16. Algoritmo EM
⎛ 1 P( j | x n ) ⎞
ΔE = −∑ ln ⎜ ∑ Pj′ P′(xn | j ) P( j | x ) ⎟
⎜ P (x ) j ⎟
n ⎝ n n ⎠
⎛ Pj′ P′(x n | j ) ⎞
≤ −∑∑ P ( j | x n ) ln ⎜
⎜ P ( x ) P( j | x ) ⎟
⎟
n j ⎝ n n ⎠
O erro pode ser minimizado através da minimização de
um upper bound para o erro com parâmetros novos:
E′ ≤ E + Q
Q ≡ −∑∑ P ( j | x n ) ln ( Pj′ P′(x n | j ) )
Com n j

17. E-step
Se o modelo for uma mistura de gaussianas
⎡ x n − μ ′j ⎤
Q ≡ −∑∑ P( j | x n ) ⎢ln ( Pj′ ) − d ln(σ ′j ) − ⎥
⎢ 2σ ′j ⎥
n j
⎣ ⎦
Assume-se uma distribuição Pj e um conjunto de
parâmetros iniciais e calcula-se a esperança acima.

18. M-Step
Minimiza-se o upper bound dado por Q sujeito ao vínculo
∑ P′ = 1
j
j
Imposto pela introdução de um multiplicador de Lagrange:
⎡N ⎤ ∂ϕ
ϕ = Q + λ ⎢ ∑ Pj ⎥ =0⇒λ = N
⎣ j =1 ⎦ ∂Pj

19. M-Step
Equações de extremo em relação aos outros parâmetros
fornecem:
∑ P( j | x ) x − μ ′
2
∂ϕ n n j
= 0 ⇒ (σ ′ ) =
12
n
∂σ ′ ∑ P( j | x )
j
j d n
n
∂ϕ 1
∂Pj′
= 0 ⇒ Pj′ =
N
∑ P( j | x
n
n )
∂ϕ ∑ P( j | x )x n n
= 0 ⇒ μ′ = n
∂μ ′ ∑ P( j | x )
j
j n
n

20. Bibiliografia
Bishop, Neural Networks for Pattern Recognition, Cap 2
Bayesian Theory
(Wiley Series in Probability and Statistics)
Jose M. Bernardo, Adrian F. M. Smith