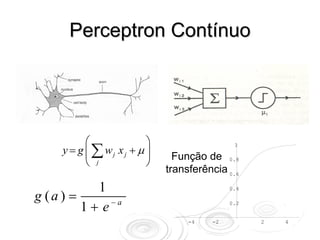
O documento discute redes neurais para classificação e regressão. Brevemente descreve a história das redes neurais, como elas podem ser usadas para classificação e regressão, e aplicações como detecção de fraude e previsão de riscos. Também resume perceptrons, redes multicamadas, e o algoritmo backpropagation para treinamento de redes neurais.

1. Redes Neurais:
Classificação e Regressão
Renato Vicente
rvicente@if.usp.br
10/01, mpmmf, IME/FEA – USP

2. RN s para Regressão e
Classificação
Breve histórico
Classificação e Regressão
Aplicações
Perceptrons
Redes Multicamada
Backpropagation

3. Uma Breve História das RNs
1943 McCuloch e Pitts Computational Neuron Model
1948 Turing B-type Unorganised Machine
1949 Hebb Aprendizado no Cérebro
1962 Rosenblatt Perceptron
1969 Minsky e Papert “Perceptrons”
1974 Werbos Backpropagation
1982 Hopfield Relação com a Física Estatística
1983 Hinton e Sejnowski Boltzmann Machines
1988 Broomhead e Lowe Redes Radial Basis
1992 MacKay e Neal Métodos Bayesianos
1996 Williams, Rasmussen e Barber Processos Gaussianos

4. Classificação e Regressão
Dado um conjunto
com N exemplos
L ={xn , t }N
n n=1
encontrar a função t = y(x, w )
*
que minimize uma
função erro w = arg min E(w)
*
estabelecida
*
Treinamento de uma RN = determinação de w

5. Aplicações
Classificação:
Rating automático para crédito
Detecção de fraudes
Sistemas de early warning para riscos
Validação automática de informações financeiras
Regressão:
Determinação de Smile de opções
Interpolação de curvas de juros
Missing data para ativos não líquidos
Detecção automática de tendências de mercado

6. Perceptron Contínuo
⎛ ⎞
y = g ⎜ ∑ wj x j + μ ⎟
1
Função de 0.8
⎝ j ⎠
transferência 0.6
1
g (a ) =
0.4
−a
1+ e 0.2
-4 -2 2 4

7. Gradient Descent
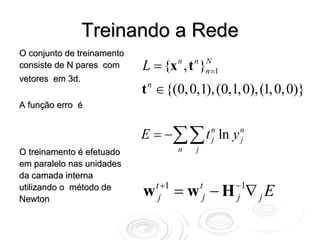
1 N
A função erro é E (w ) = ∑ [ yn (w ) − tn ]2
2 n =1
Correção na direção de
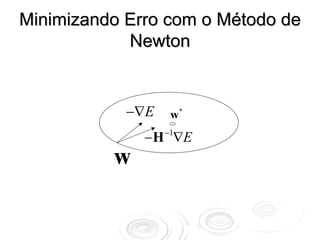
maior decréscimo w t +1 = w t − η ∇E Wt
do erro
N
∇ E = ∑ x g ′( w ⋅ x ) ( y n − t n )
n n
n =1

8. Minimização do Erro de
Treinamento
Δw (1)
E
Δw (2)
Δw (3)
w

9. Método de Newton
1
E (w ) ≅ E (w ) + (w − w ) ⋅∇E w + (w − w ) ⋅ H (w − w )
ˆ ˆ ˆ
ˆ ˆ
2
∂E
H jk = ∇E ≅ ∇E w + H ( w − w )
ˆ
∂w j ∂wk ˆ
w
ˆ
Se w* for o mínimo de E ∇E ≅ H ( w − w ) *
−1
Assim w ≅ w − H ∇E
*

10. Minimizando Erro com o Método de
Newton
−∇E w*
−1
− H ∇E
w

11. Redes Multicamada
⎛ ⎞
g 0 ⎜ ∑ w j g j (w j ⋅ x j + μ j ) ⎟
(2) (1)
⎝ j ⎠
g j ( xk , w jk )
w jk
xk

12. Exemplo1 :
Classificação com rede Softmax
j = index max{ y1 , y2 , y3 }
⎛ ⎞
exp ⎜ ∑ wkj x j ⎟
yl = ⎝ j ⎠
⎛ ⎞
∑ exp ⎜ ∑ wlj x j ⎟
l ⎝ j ⎠
x1 x2 x3

13. Treinando a Rede
O conjunto de treinamento
consiste de N pares com L = {x , t }n n N
n =1
vetores em 3d.
t ∈ {(0, 0,1), (0,1, 0), (1, 0, 0)}
n
A função erro é
E = −∑∑ t n ln y n
j j
O treinamento é efetuado n j
em paralelo nas unidades
da camada interna
t +1 −1
utilizando o método de
Newton
w j = w − H ∇ jE
t
j j

14. Regressão
Uma RN Multicamada com saída linear e um número suficientemente
grande de unidades na camada interna pode aproximar qualquer
função com precisão arbitrária. N
g ( z) g ( z0 ) + ∑ {gi +1 − gi }Θ( z − zi )
i =0
1
Θ( x )
0
x=0

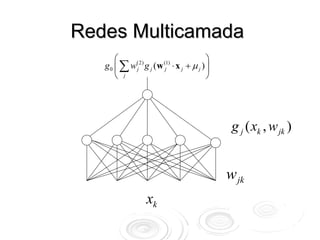
15. Exemplo 2:
Regressão não-linear em 1 dimensão
y
y = ∑ w(2) tanh( w(1) x)
j j
j
Exemplos gerados por :
tn = sen(2π xn ) + ruido
Função Erro dada por:
x 1 N
E (w ) = ∑ [ yn (w ) − tn ]2
2 n =1

16. Backpropagation:Treinando redes genéricas
y
Rede com M camadas,
cada unidade k de
camada específica m
(m,k) possui função de
transferência
g km)
(
A saída da unidade k da
camada m é
yk m )
(
X

17. Backpropagation
yk m )
(
⎛ ⎞
(m) yk m ) = g k m ) ⎜ ∑ wikm ) yi( m −1) ⎟
( ( (
g k ⎝ i ⎠
(m) ⎛ ( m −1) ⎞
= g k ⎜ ∑ wik gi (hi
(m) ( m ) ( m −1)
w
ik
)⎟
⎝ i ⎠
, onde hi( m ) ≡ ∑ wikm ) yi( m −1)
(
yi( m −1) i

18. Backpropagation
O conjunto de n n N
treinamento consiste de
{(x , t )} n=1
pares
E = ∑ ( t k − yk ( x ) )
O treinamento é efetuado 1 n n 2
através da minimização 2 k ,n
da função erro

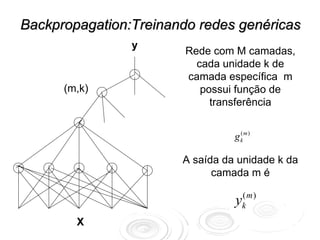
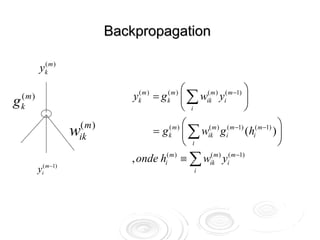
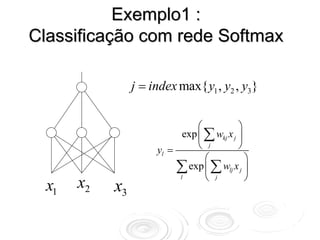
19. Backpropagation
Apresenta-se um exemplo
( x, t )
Calculam-se as saídas yk m )
(
Calculam-se os “erros” da δ (M )
k = (t − yk )[ g (M )
k ]′
camada de saída dados por
Propagam-se estes erros para
camadas interiores usando:
δ k( M −1) = (∑ wlkM )δ l( M ) )[ g k( M −1) ]′
(
l

20. Backpropagation
Atualizam-se os parâmetros utilizando:
Δwkjm ) = −ηδ k( m ) y (jm −1)
(
Repete o procedimento o mesmo
procedimento para o próximo exemplo

21. Bibliografia
Neural Networks for Pattern
Recognition
by Christopher M. Bishop
www.ncrg.aston.ac.uk