[1] Processos Gaussianos são métodos não-paramétricos para inferência e previsão que modelam a distribuição de probabilidade sobre funções. [2] Kernel models e redes neurais multicamadas podem ser vistos como aproximações de processos gaussianos quando o número de parâmetros tende ao infinito. [3] Processos gaussianos permitem fazer previsões de novas observações de forma probabilística.

1. Processos Gaussianos
Renato Vicente
Rvicente@if.usp.br
11/01, mpmmf, IME/FEA – USP

2. Gaussian Processes (GPs)
Inferência e Previsão
Método Não-Paramétrico
Splines como GPs
Kernel Models como GPs
Redes Neurais Multicamadas como GPs

3. Inferência
P(t | y;α )
x t
y
X N = { xn }n =1
N
t N = {tn }n =1
N
x w *
y ( x)
P( y ( x) | t N , X N ) ou P( w | t N , X N )

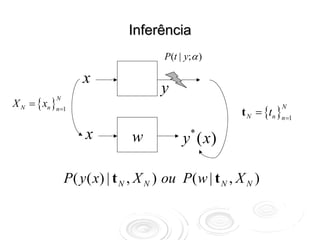
4. Previsão: aproximação
xN +1 ∉ X N w ±δ w
*
y ( xN +1 ) ± δ y
*
P(t N | w, X N ) P( w)
P( w | t N , X N ) =
P (t N | X N )
E ( w) = − ln [ P(t N | w, X N ) P( w) ]
w* = arg min E ( w)
⎡ 1 ∂2E ⎤
wamostrado de P(w*| tN , XN )exp ⎢− ∑(wj − wj *) (wk − wk *)⎥
⎢ 2 jk
⎣ ∂wj∂wk ⎥
⎦

5. Previsão: Via Monte Carlo
xN +1 ∉ X N P( w | t N , X N )
P(t N +1 | xN +1 , t N , X N )
P (t N +1 | xN +1 , t N , X N ) = ∫ d H w P(t N +1 | w, xN +1 ) P( w | t N , X N )
Gera R amostras de P ( w | t N , X N )
Via Monte Carlo:
1 R
P (t N +1 | xN +1 , t N , X N ) ≈ ∑ P(t N +1 | wR , xN +1 )
R r =1

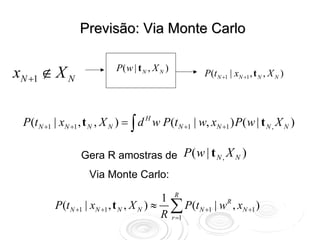
6. Métodos Não-Paramétricos
P [ t N | y ( x), X N ] P [ y ( x) ]
P [ y ( x) | t N , X N ] =
P (t N | X N )
Probabilidade no espaço de
funções
P [ y ( x) ]

7. Gaussian Process (GP)
P [ y ( x) ] é uma gaussiana
1 ⎧ 1 −1 ⎫
P ( x) = exp ⎨− x ⋅ C x ⎬
2π C ⎩ 2 ⎭
Produto escalar
funcional
1 ⎧ 1 ⎫
P[ y ] = exp ⎨− y A y ⎬
Z ⎩ 2 ⎭
Operador Linear

8. Operador Linear no espaço de funções
N
No R
y ⋅ Ax = ∑ y j Ajk xk
jk
No L2
ϕ A φ = ∫ dx ∫ dx′ ϕ ( x) A( x, x′) φ ( x′)

9. Splines e GPs
Regressão utilizando splines.
Encontrar uma função que minimize o funcional abaixo:
2
1 N
1 ⎡ d y( x) ⎤
p
E[ y ] = − β ∑ [ y(x ) − tn ] − α ∫ dx ⎢
2
dx p ⎥
n
2 n =1 2 ⎣ ⎦
AJUSTE AOS DADOS REGULARIDADE
ln P [ y | t N , X N , β , α ]
ln P [ y | α ]
ln P [ t N | y, X N , β ]

10. Splines e GPs
α
∫ dx ⎡ D
2
ln P [ y | α ] = − ⎣
p
y ( x) ⎤
⎦
2
α
=−
2 ∫ dx D p y ( x) D p y ( x)
1 † ⎡ 1 p ⎤† 1 p
= − y α 2D α 2D y
2 ⎣ ⎦
A ( x , x′ )
1 ⎡ 1 ⎤
P[ y | μ , α ] = exp ⎢ − y − μ A y − μ ⎥
Z ⎣ 2 ⎦
com μ ( x) = 0

11. Kernel Models e GPs
Um modelo de kernel é uma combinação linear de H
funções de base. Uma regressão consiste no ajuste dos
coeficientes da combinação:
H
y ( x , w ) = ∑ wh φh (x )
h =1
kernel

12. Kernel Models e GPs
Suponhamos um conjunto de N vetores (entradas):
{ xn }n=1
N
Se definirmos a matriz R com N linhas e H colunas como:
Rnh = φh ( xn )
As saídas serão
yn = ∑ Rnh wh
h

13. Kernel Models e GPs
Se supusermos que o prior sobre os parâmetros é gaussiano com
matriz de covariância totalmente simétrica:
1 ⎡ 1 ⎤
P( w ) = exp ⎢ − 2 w ⋅ w ⎥
2π σ 2 I ⎣ 2σ ⎦
A covariância das funções y representada pelos modelos de kernel
será:
Qnm = yn ym = ∑R
j
nj w j ∑ Rmk wk = ∑∑ Rnj Rmk w j wk
k j k
=σ 2δ jk
= σ 2 ∑ Rnj Rmj
j

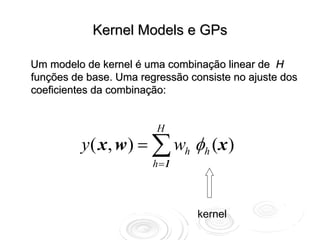
14. Kernel Models
{ xn }n=1
N
Para qualquer conjunto de N vetores
P( w ) gaussiana implica em
P ( y ( x1 ), , y ( x N )) gaussiana
P[ y ] é um processo gaussiano

15. Exemplo: Mistura de Gaussianas em 1d
Suponhamos a seguinte forma para o kernel:
⎡ 1 2⎤
φh ( x) = exp ⎢ − 2 ( x − ch ) ⎥
⎣ 2r ⎦
A covariância de P(y) será:
⎡ ( xn − c j ) 2 ⎤ ⎡ ( xm − c j ) 2 ⎤
Qnm = σ 2 ∑ exp ⎢ − 2 ⎥ exp ⎢ − 2 ⎥
j ⎢
⎣ 2r ⎥
⎦ ⎢
⎣ 2r ⎥
⎦
σ 2 cmax ⎡ ( xn − c) 2 ⎤ ⎡ ( xm − c) 2 ⎤
= ∑ Δc exp ⎢− 2 r 2 ⎥ exp ⎢− 2 r 2 ⎥
Δc c =cmin ⎣ ⎦ ⎣ ⎦

16. Exemplo: Mistura de Gaussianas em 1d
Levando ao limite de infinitas funções de base H → ∞
com Δc → 0 e σ2 podemos substituir
=S 2
Δc
a soma por uma integral
⎡ ( xn − c) 2 ⎤ ⎡ ( xm − c) 2 ⎤
cmax
Qnm = S ∫ dc exp ⎢ −
2
2 ⎥ exp ⎢ − ⎥
cmin ⎣ 2r ⎦ ⎣ 2r 2 ⎦
⎡ ( xn − xm ) 2 ⎤
=S 2
π r exp ⎢ −
2
2 ⎥ = C ( xn , xm )
⎣ 4r ⎦

17. Redes Neurais Multicamada e GPs
Uma rede neural com uma camada escondida e saída linear
representa a seguinte família de funções:
H
⎛ I ( 1) ( 1) ⎞
y ( x; w ) = ∑ wh tanh ⎜ ∑ whi xi + wh 0 ⎟ + w02 )
(2) (
h=1 ⎝ i =1 ⎠
Se uma distribuição a priori gaussiana para os parâmetros w é
assumida, P[y] tende para um processo gaussiano conforme
H →∞
(R. Neal, Priors for Infinite Networks)

18. Bibliografia
Neal, R. M. (1994) ``Priors for infinite networks'', Technical
Report CRG-TR-94-1, Dept. of Computer Science, University of
Toronto (http://www.cs.utoronto.ca/~radford/publications.html)
D. MacKay Introduction to Gaussian Processes
(http://wol.ra.phy.cam.ac.uk/mackay/BayesGP.html)
M. Gibbs Bayesian Gaussian Processes for Regression and
Classification (PhD Thesis, University of Cambridge)
(http://wol.ra.phy.cam.ac.uk/mng10/GP/GP.html)
Veja também: http://www.gatsby.ucl.ac.uk/~edward/gp/