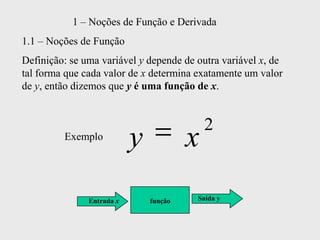
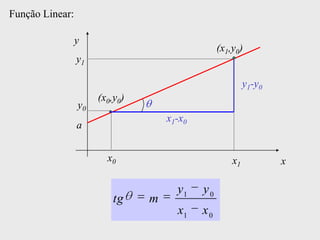
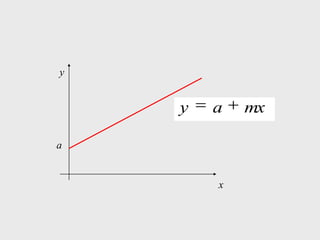
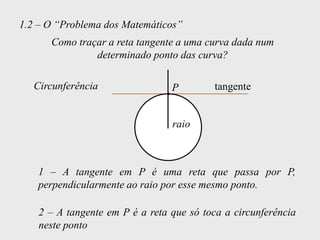
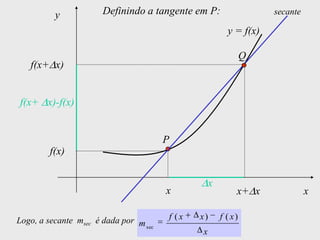
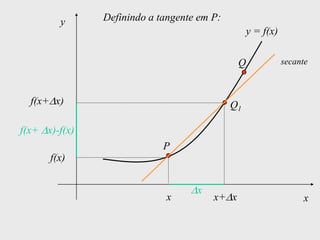
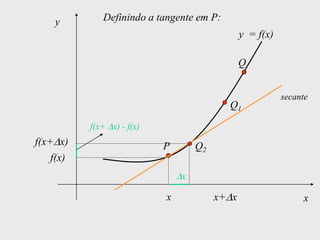
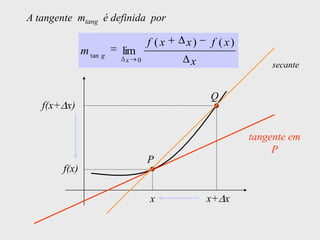
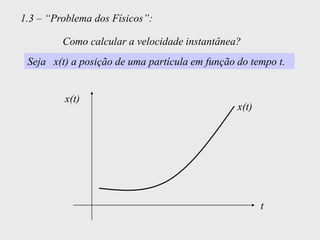
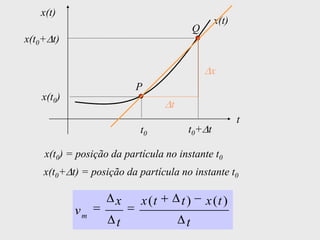
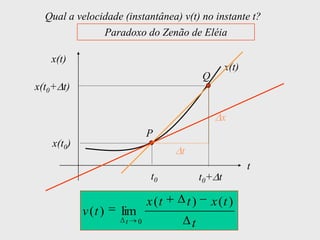
[1] Curso de Especialização em Telecomunicações que aborda noções de função, derivada, suas definições e regras de derivação; [2] A derivada representa a taxa instantânea de variação de uma função e é usada para calcular a velocidade de um móvel a partir de sua posição em função do tempo; [3] O documento explica como calcular a derivada da posição x(t) = 3 + 0,5t - 3t2 no instante t = 10,0s para obter a velocidade do móvel nesse ponto.

1. Curso de Especialização em Telecomunicações
Tersio Guilherme de Souza Cruz

2. 1 – Noções de Função e Derivada
1.1 – Noções de Função
Definição: se uma variável y depende de outra variável x, de
tal forma que cada valor de x determina exatamente um valor
de y, então dizemos que y é uma função de x.
2
Exemplo
y x
Entrada x função Saída y

3. x y
0 0
1 1
2
y x 4 2
-1 1
-2 4

4. Outros exemplos:
y cos x ou y( x) cos x
1 2
x xo vot 2
at
ou
1 2
x (t ) xo vot 2
at
1
q1 q 2
E (r ) 4 2
0
r

5. Seja a posição x de um móvel em MRUV em função do tempo
t dada pela equação
2
x (t ) 5 10 t 2t
Então, a posição do móvel no instante t = 1,0 s é
2
x (1, 0 ) 5 10 (1, 0 ) 2 (1, 0 )
x (1, 0 ) 5 10 , 0 2 ,0
x (10 ) 13 m

6. Função Linear:
y
(x1,y0)
y1
y1-y0
(x0,y0)
y0
x1-x0
a
x0 x1 x
y1 y0
tg m
x1 x0

7. y1 y0 m ( x1 x0 )
y1 y0 m ( x1 x0 )
y a mx
com a = y0 – mx0

8. y
y a mx
a
x

9. 1.2 – Nocões de Derivada
Origens do Cálculo
-Kepler, Galileu, Simon Stevin, Pièrre de Fermat, René Descartes,
Blaise Pascal ....
Isaac Newton (1642 – 1727)
Gottfried Wilhelm Leibnz
(1646 – 1716)

10. 1.2 – O “Problema dos Matemáticos”
Como traçar a reta tangente a uma curva dada num
determinado ponto das curva?
Circunferência P tangente
raio
1 – A tangente em P é uma reta que passa por P,
perpendicularmente ao raio por esse mesmo ponto.
2 – A tangente em P é a reta que só toca a circunferência
neste ponto

11. Outras curvas: problemas!
P
P
Qual o raio? Tangente?
P
Tangente. Mas toca duas vezes a reta

12. y Definindo a tangente em P: secante
y = f(x)
Q
f(x+ x)
f(x+ x)-f(x)
P
f(x)
x
x x+ x x
Logo, a secante msec é dada por m f (x x) f ( x)
sec
x

13. y Definindo a tangente em P:
y = f(x)
Q secante
f(x+ x) Q1
f(x+ x)-f(x)
P
f(x)
x
x x+ x x

14. y Definindo a tangente em P:
y = f(x)
Q
secante
Q1
f(x+ x) - f(x)
f(x+ x) P Q2
f(x)
x
x x+ x x

15. A tangente mtang é definida por
f (x x) f ( x)
m tan g lim
x 0 x secante
Q
f(x+ x)
tangente em
P
P
f(x)
x x+ x

16. 1.3 – “Problema dos Físicos”:
Como calcular a velocidade instantânea?
Seja x(t) a posição de uma partícula em função do tempo t.
x(t)
x(t)
t

17. x(t)
x(t)
Q
x(t0+ t)
x
P
x(t0)
t
t
t0 t0+ t
x(t0) = posição da partícula no instante t0
x(t0+ t) = posição da partícula no instante t0
x x (t t) x (t )
vm
t t

18. Qual a velocidade (instantânea) v(t) no instante t?
Paradoxo do Zenão de Eléia
x(t)
x(t)
Q
x(t0+ t)
x
P
x(t0)
t
t
t0 t0+ t
x (t t) x (t )
v (t ) lim
t 0 t

19. 1.4 - Definição de derivada
A derivada de uma função f é a função f´ tal que o seu valor
em qualquer número x do domínio de f seja dado por
´ df x (t t) x (t )
f lim
dx t 0 t
se este limite existir
Uma função derivável em um ponto pode ser não-derivável em
outro!!!!

20. Duas Interpretações:
1- A derivada f´ de uma função é uma função cujo valor em x é a
inclinação da reta tangente ao gráfico de y = f(x) em x.
2 – A derivada f´ é uma função cujo valor em x é a taxa
instantânea da variação de y com relação a x no ponto x.
Exemplos:
dx dQ
v (t ) I (t )
dt dt

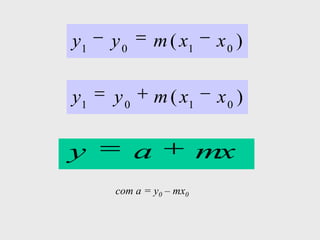
21. d
v (t ) [ x ( t )]
x(t) dt
v(t1)= 0
v(t1)
v(t0) 0
v(t0)
v(t2) v(t2) 0
t
t0 t1 t2

22. Exemplo usando a definição: calcule a derivada da função
f(x) = 3+x2
f (x x) f ( x)
f´ lim
x 0 x
2 2 2
3 (x x) 3 x x 2x x
f (x x)
x x
2
x 2x x
f´ lim [ ] lim [ x 2 x] 2x
x 0 x x 0
df d d 2
f´ [ f ( x )] [3 x ] 2x
dx dx dx

23. 1.5 - Algumas regras de derivação
1.5.1 - Regra da Constante: para qualquer constante c
y
d
(c ) 0 y=c
dx c
Inclinação = 0
x
1.5.2 - Regra da Potência: para qualquer número real n
d n n 1 Ver exemplo
(x ) nx anterior
dx

24. 1.5.3 - Regra da Multiplicação por uma Constante:se c é uma
constante e f(x) é uma função derivável no ponto x, cf(x) também
é uma função derivável e
d
[ cf ( x )] cf ( x )
dx
Exemplo: seja
2
f ( x) cx
d 2
( cx ) 2 cx
dx

25. 1.5.4 - Regra da Soma:se f(x) e g(x) são duas funções deriváveis
no ponto x, a soma s(x) = f(x) + g(x) também é derivável e
s´( x ) f ´( x ) g ´( x )
d d d
[ f ( x) g ( x )] [ f ( x )] [ g ( x )]
dx dx dx
2
Exemplo: seja a função x (t ) 10 4t 5t
f(x) = 10 g(x) = 4t h(x) = -5t 2
d 2
(10 4t 5t ) 0 4 10 t 4 10 t
dx

26. 1.5.5 - Regra da Produto:se f(x) e g(x) são duas funções
deriváveis no ponto x, o produto P(x) = f(x) . g(x) também é
derivável e
( f . g )´ fg ´ g . f ´
d dg df
[ f ( x ). g ( x )] f ( x ). g ( x ).
dx dx dx
2
Exemplo: seja a função P ( x) x (3 x 1)
f(x) = x2 g(x) =3x+1
2 2
P ´( x ) ( x ).( 3 ) (3 x 1).( 2 x ) 9x 2x

27. 1.5.6 - Regra da Quociente:se f(x) e g(x) são duas funções
deriváveis no ponto x, o quociente P(x) = f(x) / g(x) também é
derivável e
f g . f ´ fg ´
( )´ 2
com 0
g g
df dg
g ( x ). f ( x ).
d f ( x) dx dx
2
dx g ( x) g ( x)
2
Exemplo: seja a função y (x 2x 21 ) /( x 3)
2 2
(x 3 ).( 2 x 2) (x 2x 21 .(1)] x 6x 15
Q ´( x ) 2 2
(x 3) (x 3)

28. 1.5.7 - Regra da Cadeia:se g(x) for derivável em x e a função f
for derivável em g(x), então a função composta f o g será
derivável em x, e
( f  g )`( x ) f ´( g ( x )). g ´( x )
dy dy du
dx du dx
Exemplos:
2
a) Seja a função y x 1
1
2
u x 1 y u (u ) 2

29. dy 1 1 1 2
1 1
(u ) 2
(x 1) 2
2
du 2 2 2 x 1
du
2x
dx
dy 1 x
(2 x)
2 2
dx 2 x 1 x 1

30. b) Seja a função geral do tipo
n
y f ( x)
n
u f ( x) e y u
dy n 1 du
nu f ´( x )
du dx
dy dy du n 1
nu f ´( x )
dx du dx

31. 1.5.8 – Funções Trigonométricas
f ( x) sen u
df ( x ) du
d (sen u ) cos u
dx dx
f ( x) cos u
df ( x ) du
d (cos u ) sen u
dx dx

32. f ( x) tgu
sen u Regra do
f ( x) quociente
cos u
d 2 du
( tgu ) sec u
dx dx

33. Exemplo: seja a função
y sen( 10 x 3)
Vamos introduzir a variável intermediária
du
u 10 x 3 10
dx
dy
y sen u cos u cos( 10 x 3)
du
dy dy du
10 cos( 10 x 3)
dx du dx

34. Exemplo: seja a função
2
y sen x 1
2
u x 1 y sen u
dy dy du
Regra da cadeia
dx du dx
dy dy 2
cos u cos x 1
du du

35. 1
2
dy du d (x 1) 2
cos u
du dx dx
1
2 du d (z ) 2
z x 1
dx dx
du du dz 1
1 x
2
z 2
2x
2
dx dz dx x 1
2
dy dy du x cos x 1
2
dx du dx x 1

36. 1.5.9 – Função Logarítmica : se u é uma função diferenciável de x
e u(x) 0, então
d 1 du
[ln u ]
dx u dx

37. Exemplo: seja a função
3
y ln( x 2x 1)
3
u x 2x 1 y ln u
dy 1 1 du 2
3
3x 2
du u x 2x 1 dx
2
dy 3x 2
3
dx x 2x 1

38. 1.5.10 – Função Exponencial : se u é uma função diferenciável
de x, então
d u u du
[e ] e
dx dx
Exemplo: seja a função 1
2
y e x
1 du 2
u 2 3
x
dx x
dy d u u du 2 1
2
[e ] e 3
e x
dx dx dx x

39. 1.6 - Derivada no ponto: seja a posição de um móvel dada pela
função
2
x (t ) 3 0 ,5 t 3t
com x dado em metros. Calcule a velocidade do móvel no
instante t = 10,0s.
dx
v (t )
dt
dx
v (10 , 0 ) 0 ,5 6t t 10 , 0
0 ,5 6 (10 , 0 )
dt t 10 , 0
v (t ) 60 ,5 m

40. 1.7 - Derivadas de Ordem Superior: se a função f for
derivável, então f´ é chamada de derivada primeira de f. Se a
derivada f´ existir, ela será chamada de derivada segunda de f e
poderá ser denotada por f´´.
A derivada enésima da função f (n=inteiro positivo e maior do
que 1), é a derivada primeira da derivada (n-1)ésima de f.
Notação de Leibniz
df derivada 3
d f derivada
primeira
dx dx
3 terceira
2 n
d f derivada d f derivada
2 segunda n enésima
dx dx

41. Exemplo: no MRUV a posição da partícula é dada por
1 2
x (t ) x0 v0t 2
at
em que x0 (posição inicial), v0 (velocidade inicial) e a
(aceleração) são constantes.
dx
v (t ) vo at
dt
2
dv d x
a (t ) 2
a
dt dt

42. 1.8 – Derivadas Parciais: seja a função escalar (x,y,z) no
espaço. As derivadas parciais de em relação a x, y e z são,
respectivamente,
: lê-se “del”
x y z
Exemplo: seja a função
2 3
f ( x, y ) x y
2
2x 3x
x y

43. Exemplo: a equação de uma onda numa corda vibrante é
dada por
y ( x, t ) y m cos( kx t)
com ym, k e constantes.
A velocidade vertical de um ponto localizado no ponto x
(fixo) da corda é dada por
y
vy [ y m cos( kx t )]
t t
vy y m [ sen( kx t )].( )
vy y m sen( kx t)

44. A aceleração vertical deste ponto é dada por
2
y
ay 2
[ y m sen( kx t )]
t t
ay y m [cos( kx t )].( )
2
ay y m cos( kx t)