Redes neurais com matlab

Redes Neurais para Inferência Estatística
-F E A / U S P J u n / 2 0 0 2
Renato Vicente∗

Programa

1. Introdução: Redes Neurais, Matlab e Netlab
2. Algoritmos de Otimização
3. Estimação de Densidades de Probabilidade
4. Redes Neurais com uma Camada
5. Redes Neurais Multicamada
6. Amostragem
7. Técnicas Bayesianas

Opcionalmente:

8. Radial Basis Functions
9. Redução Dimensional e Visualização de dados
10. Processos Gaussianos

Referências Básicas:

• Using Matlab, The MathWorks Inc. (2000);
• Bishop, C.M., Neural Networks for Pattern Recognition, Oxford University
Press, Oxford, 1995;
• Nabney, I.T., Netlab: Algorithms for Pattern Recognition, Springer,
London, 2002.

∗
rvicente@usp.br

Criado por Renato Vicente 1 27/01/06

Introdução: Redes Neurais, Matlab e Netlab

Redes Neurais

Rede Neural é um nome fantasia para modelos de inferência multidimensionais e não-
lineares. O grande apelo destes modelos está em sua capacidade de “aprender”, generalizar
ou extrair regras automaticamente de conjuntos de dados complexos.

No caso mais simples, temos um conjunto de pares entrada-saída D = {( x(n ) , t (n ) )}n =1 e
p

queremos modelar a função t = y = y (x, w ) que produz melhores estimativas para pares
ˆ
fora do conjunto D , dados vetores x. Este problema é denominado r e g r e s s ã o . A Rede
Neural consiste simplesmente de uma escolha particular para a família de funções
y( x , w ) parametrizada por w, denominados p e s o s s i n á p t i c o s .

A importância das Redes Neurais neste contexto está no fato delas representarem um
esquema bastante genérico para a representação de famílias de funções não-lineares com
várias variáveis de entrada e saída e controladas por um certo número de parâmetros
ajustáveis.

Há uma série de famílias, ou arquiteturas, clássicas para Redes Neurais que são
representadas graficamente.

P e r c e p t r o n L i n e a r P e r c e p t r o n N ã o -lin e a r
N
 N 
y = ∑ w j x j + w0 y = g  ∑ w j x j + w0 
j =1
 j =1 

1 x 1 x

R e d e M u lticam a d a

 n  N 
y = g  ∑ u l g 1  ∑ w j x j + w0  
 l =1 
  j =1 


É possível 1 mostrar que Redes Neurais Multicamada com um número N suficientemente
grande de unidades na mamada interna (ou escondida) podem representar qualquer
função com erro menor que ε ( N ) . Uma maneira simples e direta para percebermos este
fato é ilustrada abaixo:
N

∑{
g ( z ) ≈ g ( z0 ) +Θ ( x)gi +1 − gi }Θ ( z − zi )
1
i =0

0
0
x=0
x=0

Na figura uma função arbitrária g(z) é representada por uma soma de funções degrau
Θ( z − zi ) sobre uma partição da reta P = {z0 , z1,..., z N }. A medida que refinamos a
partição fazendo zi +1 − zi < δ ( N ) , reduzimos o erro ε ( N ) .

Quando as saídas consistem de classes discretas t ∈ {1,..., c} o problema de inferência é
denominado c l a s s i f i c a ç ã o .

1
Hornik, K. (1991). Approximation capabilities of multilayer feedforward networks. Neural Networks 4 (2),
251-257.


Matlab

Matlab (M a t r i x L a b o r a t o r y ) é uma linguagem para computação científica com estrutura
otimizada para a realização de operações com matrizes. O ambiente Matlab é composto
por uma série de funções pré-definidas para cálculo, leitura e escrita de arquivos e
visualização. Este conjunto de funções pode ser facilmente extendido por t o o l b o x e s
dedicadas. Há t o o l b o x e s para finanças, tratamento de sinais, econometria e redes neurais.

Para ilustrar a forma como matrizes podem ser tratadas pelo Matlab utilizamos o
quadrado mágico de Dührer que é utilizado como exemplo no G e t S t a r t que acompanha
o software. Na linha de comando do Matlab entramos:

> A = [16 3 2 13; 5 10 11 8; 9 6 7 12; 4 15 14 1]

A=
16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1

Após este comando a matriz A fica armazenada no W o r k s p a c e do Matlab conforme
ilustrado abaixo.


As propriedades do quadadro mágico podem ser analisadas utilizando funções do Matlab.
Por exemplo, a função abaixo soma cada uma das linhas da matriz A.

> sum (A)

ans =
34 34 34 34

Na ausência de definição de variável de saída o Matlab aloca o resultado no W o r k s p a c e
sob o nome a n s . Assim ao entrarmos
> ans

ans =
34 34 34 34

Se quisermos somar as colunas ao invés das linhas temos que transpor a matriz A, isso
feito simplesmente pelo comando

>A'

ans =
16 5 9 4
3 10 6 15
2 11 7 14
13 8 12 1

Assim podemos realizar a soma das colunas entrando

>sum(A')'

ans =
34
34
34
34

Novamente o resultado é 34. Podemos também calcular a soma da diagonal, ou traço,
de duas formas:

> diag (A)

ans =
16
10
7
1


> sum (diag(A))

ans =
34

Ou

> trace(A)

ans =
34

Curiosamente continuamos obtendo 34. Somemos agora a antidiagonal da matriz A, para
isso podemos utilizar a função f l i p l r para enviarmos cada coluna da esquerda para a
direita da matriz A.

> fliplr (A)

ans =
13 2 3 16
8 11 10 5
12 7 6 9
1 14 15 4

E a seguir

> sum(diag(fliplr(A)))

ans =
34

As somas são sempre iguais a 34 pois quando dividimos números inteiros de 1 a 16 em
quatro grupos com somas iguais temos:

> t=1:1:16

t=
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

> sum(t)/4

ans =
34

Aqui utilizamos ":" para gerarmos números de 1 a 16 em passos de 1.


O Matlab possui uma função específica para a criação de quadrados mágicos de qualquer
dimensão, esta função é

> B=magic(4)

B=
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1

É possível reordenar as colunas de B para reobtermos A utilizando o comando

> B(:,[1 3 2 4])

ans =
16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1

Netlab

O Netlab é uma t o o l b o x para Redes Neurais para Matlab disponibilizada gratuitamente
no site do Neural Computing Research Group da Univerisdade de Aston
(www.ncrg.aston.ac.uk). Esta t o o l b o x toran a implementação de modelos baseados em
Redes Neurais muito simples. Os códigos produzidos em Matlab podem então ser
convertidos em executáveis utilizando o M a t l a b C o m p i l e r . Como um primeiro contato
com o Netlab escreveremos sua versão para o clássico "H e l l o W o r l d ".

Começamos por gerar de um conjunto de dados fictícios para treinamento de nossa
Rede Neural. Para isso vamos supor que a função que queremos inferir é
f ( x) = sin (2π x ) . No entanto, só temos acesso a uma versão corrompida por ruído
gaussiando desta função assim, nosso conjunto de dados é "gerado" da seguinte forma:
tn = sin(2π xn ) + σε n
,
ε n ~ N (0,1)
onde N(0,1) é uma distribuição normal com média nula e variância unitária.

No Matlab teremos

1 x=[0:1/19:1]';
2 ndata=size(x,1);
3 t=sin(2*pi*x) + 0.15*randn(ndata,1);


Aqui utilizamos alguns recursos novos. Utilizamos ao final de cada linha ";" , esta
instrução faz com que o Matlab omita resultados intermediários dos cálculos sendo
executados. A primeira instrução gera um vetor coluna x com 20 dimensões contendo
números de 0 a 1 em intervalos de 1/19. Na linha 2 utilizamos a função s i z e ( x , 1 ) para
obtermos o tamnho em número de linhas do vetor coluna x, assim, se entrarmos:

> size(x)

ans =
20 1

Ou seja, o vetor x possui 20 linhas e 1 coluna, s i z e ( x , 1 ) nos dá o número de linhas,
enquanto s i z e ( x , 2 ) nos dá o número de colunas. Na linha 3 utilizamos a função
r a n d n ( l i n h a s , c o l s ) para gerarmos um vetor de números aleatórios independentes com
distribuição gaussiana com média nula e variância unitária. De forma genérica esta
instrução pode ser empregada pra gerar matrizes aleatórias de qualquer tamanho.

>ran dn(5,5)

ans =
1.3808 0.3908 -1.3745 -1.3454 -0.7826
1.3198 0.0203 -0.8393 1.4819 -0.7673
-0.9094 -0.4060 -0.2086 0.0327 -0.1072
-2.3056 -1.5349 0.7559 1.8705 -0.9771
1.7887 0.2214 0.3757 -1.2090 -0.9640

No Matlab, podemos visualizar o vetor t e a função original utilizando:

> plot(x,sin(2*pi*x),x,t,'k+');

1.5

1

0.5

0

-0.5

-1

-1.5
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

Gerado nosso conjunto fictício de dados, podemos definir uma arquitetura de rede para
utilizarmos na inferência. Assumiremos aqui que uma Rede Neural Multicamada com 3


unidades na camada escondida seja adequada. No Netlab podemos definir uma
arquitetura de rede em uma única linha de comando.

4 net=mlp (1, 3, 1, 'linear')

net =
type: 'mlp'
nin: 1
nhidden: 3
nout: 1
nwts: 10
actfn: 'linear'
w1: [-1.6823 -0.5927 0.1820]
b1: [-0.1300 -0.1185 -0.0827]
w2: [3x1 double]
b2: 0.2541

A função m l p do Netlab cria uma estrutura que especifica completamente a arquitetura
e os parâmetros iniciais da Rede Neural. Assim a rede possui n i n = 1 entrada, n h i d d e n = 3
unidades na camada interna, n o u t = 1 saída e n w t s = 1 0 parâmetros entre pesos sinápticos e
limiares. Os parâmetros são iniciados em valores aleatórios. Graficamente teremos:

Cada unidade possui uma entrada extra denotada por uma seta que regula o l i m i a r d e
d i s p a r o de cada um dos neurônios. Cada neurônio da camada escondida gerado pela
função m l p implementa uma f u n ç ã o d e t r a n s f e r ê n c i a s i g m o i d a l do tipo tanh(b + ∑ w j x j ) .
j

Já o neurônio da camada de saída implementa a função de transferência especificada na
função m l p , no caso, uma função linear. Assim, a arquitetura da Rede Neural que
utilizaremos representa a seguinte família de funções:

3
y( x, w, b ) = b2 + ∑ w2 l tanh(b1l + w1l x) .
l =1
O terceiro passo consiste no treinamento desta rede utilizando os dados fictícios
contidos no conjunto de treinamento. Para isso o Netlab utiliza a infra-estrutura de
algoritmos de otimização do Matlab. Primeiro é necessário armazenar as configurações
padrão dos otimizadores do Matlab:


5 options=foptions;

A seguir personalizamos algumas destas opções:

6 options(1) = 0;

Este comando evita que os algoritmos de otimização exibam na tela a evolução passo a
passo da função custo sendo minimizada.

7 options(14) =100;

Esta instrução limita em 100 passos os ciclos de otimização. Agora podemos treinar nossa
rede utilizando a função n e t o p t do Netlab:

8 [net, options] = netopt(net, options, x, t, 'scg');

Warning: Maximum number of iterations has been exceeded

A função n e t o p t otimiza os parâmetros da rede definida pela estrutura n e t , utilizando as
opções de otimizador defindas em o p t i o n s e utilizando os dados de entrada contidos no
vetor x e de saída contidos no vetor t . O último argumento em n e t o p t especifica o tipo
de algoritmo a ser utilizado na otimização, no exemplo, 's c g ' significa s c a l e d g r a d i e n t . A
função retorna uma mensagem de aviso indicando que a otimização foi terminada devido
ao limite de 100 passos de otimização.

Neste momento já obtivemos no W o r k s p a c e do Matlab uma estrutura n e t com
parâmetros otimizados assim:

> net.w1

ans =
-5.2017 0.8701 1.5318

> net.w2

ans =
2.6033
1.0716
3.4209

> net.b1

ans =
2.4785 -0.6179 -0.3766

> net.b2

ans =
-0.7588


O quarto passo consiste em utilizarmos a rede recém treinada. Para isso utilizamos a
função m l p f w d do Netlab, assim se quisermos saber qual seria a saída para a entrada
x = 0 . 5 6 5 , calculamos:

>mlpfwd(net,0.565)

ans =
-0.4632

Para analisarmos visualmente a qualidade de nosso modelo para os dados representamso
em um gráfico previsões para várias entradas e o valor "real":

9 plotvals=[0:0.01:1]';
10 y=mlpfwd(net,plotvals);
11 plot(plotvals, y, 'ob',plotvals,sin(2*pi*plotvals));

1.5

1

0.5

0

-0.5

-1
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

Na figura acima as previsões aparecem como circunferências e o valor "real" como uma
linha cheia. A qualidade da previsão irá depender da Rede Neural empregada e do nível
de ruído dos dados.


Toda a seção de Matlab, utilizada neste problema pode ser armazenada na forma de um
arquivo .m como o exibido a seguir:

Exercícios

(1) Escreva uma rotina ou função em Matlab que calcule o erro quadrático de predição da
Rede Neural Multicamada utilizada no exemplo acima no conjunto p l o t v a l .

E ( x) = ∑  f ( x j ) − y( x j; w b)  .
2
 , 
j

(2) Treine Redes Multicamada com número de unidades na camada interna indo de
n h i d d e n = 1 a n h i d d e n = 30 e construa um gráfico do erro de predição acima contra o
número de unidades na camada escondida. Qual é a melhor escolha de arquitetura ?


Algoritmos de Otimização

Aprendizado em Redes Neurais: Um Problema de Otimização

Como já dissemos, o problema de regressão utilizando Redes Neurais consiste em
encontrar a função tˆ = y (x, w ) que produz melhores estimativas para a regra implícita
em um conjunto de exemplo de pares entrada-saída D = {(x ( n ) , t ( n ) )}n=1 .
p

É importante ressaltar que a tarefa central de uma regressão não é a memorização do
conjunto de exemplos D, mas sim a antecipação de pares novos (ou fora da amostra) que
poderiam ser gerados pelo mesmo processo que gerou D.

A descrição completa do processo gerador do conjunto D é fornecida por uma densidade de
probabilidade conjunta p (x, t ) sobre D. Esta densidade de probabilidade pode ser
decomposta da seguinte forma:
p (x, t ) = p (t x) p (x) (1.1)

A densidade p (t x) é conhecida como densidade condicional e representa a probabilidade
de uma saída t dada uma entrada com valor específico x. Já a densidade p(x) representa a
densidade incondicional de x que pode ser calculada a partir da densidade conjunta por
integração (també conhecida como marginalização):
p (x) = ∫ p (t, x) dt (1.2)

Uma maneira pictórica de representarmos um modelo para o processo de geração do
conjunto de dados D é exibida na figura a seguir:

Processo
estocástico Processo Saídas
de geração determinístico de corrompidas
de entradas geração de saídas por ruído
x y(x) t
ruído

No modelo acima há dois processos estocásticos: o de geração das entradas x descrito pela
densidade p(x) e o de geração de saídas com ruído descrito pela densidade condicional
p (t x ) .

Criado por Renato Vicente 10/06/02
13

O aprendizado consiste em estimarmos a densidade condicional de probabilidade p (t x)
que melhor se ajuste ao conjunto D, possibilitando assim a predição de saídas possíveis
para entradas x fora do conjunto D utilizado no treinamento.

Ao modelarmos os dados utilizando Redes Neurais supomos uma arquitetura de rede, o que
equivale à escolha de uma família de funções y (x; w ) parametrizada por w. Por
conseqüência a densidade condicional p (t x; w ) também é parametrizada por w. Para
encontrarmos qual é o vetor w que melhor ajusta os dados em D, podemos maximizar a
função de verossimilhança definida por:

p
L(w ) = ∏ p(x n , t n ; w )
n =1
p
(1.3)
= ∏ p (t x ; w ) p ( x )
n n n

n =1
Alternativamente, e com uma série de vantagens práticas podemos definir uma função erro
que deve ser minimizada no aprendizado:

E (w ) = − ln L(w )
p p
(1.4)
= −∑ ln p(t n x n ; w ) − ∑ ln p (x n )
n =1 n =1
O segundo somatório não depende do vetor de parâmetros w, podendo ser ignorado na
minimização do erro E(w):

p
E (w ) = −∑ ln p (t n x n ; w ) (1.5)
n =1

O aprendizado em uma Rede Neural consiste simplemente em uma tarefa de otimização:
minimizar E(w) dado o modelo o conjunto de treinamento D e a densidade condicional
p(t x; w ) .

Erro quadrático

Suponhamos que o processo real de produção de saídas t consista de uma perturbação
estocástica ε sobre uma função determinística h(x) assim:

t = h( x) + ε (1.6)

Suponhamos agora que a perturbação estocástica (ruído) seja distribuída de forma
normal:

14

 ε2  1
p (ε ) = exp  − 2  (1.7)
2πσ 2  2σ 
Se modelarmos a função real com uma Rede Neural cuja arquitetura implemente a
família y (x; w ) a densidade condicional será :
1  (t − y (x; w ) )2 
p(t x) = exp  − . (1.8)
2πσ 2 
 2σ 2 


O erro será então :
p
E (w ) = −∑ ln p (t n x n ; w )
n =1
(1.9)
∑ (t − y (x; w) ) + Np ln σ + 2 ln(2π )
p
1 2 Np
= n

2σ 2 n =1

Ao omitirmos as constantes e o fator de escala em frente ao somatório teremos a
seguinte medida de erro de aprendizado:
E ( w ) = ∑ (t n − y ( x n ; w ) ) ,
1 p 2
(1.10)
2 n =1
que é a distância Euclidiana clássica utilizada em regressões usuais.

Erro r-Minkowski

Se supusermos que o ruído ε é distribuído segundo uma generalização de uma
gaussiana:
1

p (ε ) =
rβ r
2Γ(1/ r )
exp − β ε ( r
) (1.11)

O erro de treinamento tomará a seguinte forma:

∑ (t − y ( x n ; w ) ) .
1 p n r
E (w ) = (1.12)
2 n =1

A figura abaixo representa densidades para vários valores de r.

15

A escolha de diferentes valores para o parâmetro r regula a sensibilidade do modelo a
valores com erros grandes, como pode ser visto na figura abaixo:

Conforme r aumenta maior é a penalização para desvios grandes que passam, por serem
pouco prováveis, a ser considerados incompatíveis com os dados.

Exercícios

(1) Generalize (1.10) para o caso de saídas t multidimensionais.
(2) Demonstre a expressão (1.12) para a função erro r-Minkowski.

16

Otimização

Há várias técnicas para otimização de funções multidimensionais e não-lineares como a
função erro que devemos minimizar. Genericamente um algoritmo iterativo de
otimização no espaço de parâmetros w consiste em uma busca onde a cada passo são
determinados uma direção e um tamanho de passo:

w t +1 = w t + α t d t (1.13)
Quanto mais informação sobre a geometria da superfície definida pela função erro E(w)
for utilizada mais eficiente será o algoritmo. Uma boa idéia de como um algoritmo de
otimização pode utilizar a geometria da função erro pode ser obtida utilizando uma
aproximação quadrática para a superfície. Consideremos a seguinte expansão em torno de
um ponto w :ˆ
1
E (w ) ≅ E (w ) + (w − w ) ⋅∇E (w ) + (w − w ) ⋅ H (w − w )
ˆ ˆ ˆ ˆ ˆ (1.14)
2
A matriz H é conhecida como Hessiano sendo definida como:

∂2E
H jk = (1.15)
∂w j ∂wk ˆ
w

Suponha que w = w seja um extremo de E, então:
ˆ *

1
E (w ) ≅ E (w* ) + (w − w* ) ⋅ H (w − w* ) (1.16)
2

Podemos calcular os autovetores do Hessiano H :
Hu k = λk u k , (1.17)
onde
u j ⋅ u k = δ jk . (1.18)
Podemos expandir o vetor w – w* na base dos autovetores de H para escrevermos:
w − w* = ∑ α k u k (1.19)
k
Substituindo (1.19) em (1.16) e utilizando (1.17) e (1.18) :
1
E (w ) ≅ E (w* ) + ∑ λkα k2 . (1.20)
2 k
Assim, os autovetores da Hessiana indicam direções ortogonais que diagonalizam a
matriz H. De (1.20) pode-se concluir que para que w* defina um mínimo é necessário
que todos os autovalores sejam positivos, além disso a velocidade de convergência do
erro é maior em direções com autovalor maior.

Otimização em Netlab

17

Discutiremos quatro técnicas implementadas pelo Netlab:

1. Gradient Descent
2. Gradiente Conjugado
3. Gradiente Conjugado Escalado
4. Quase-Newton

Para exemplificarmos como Netlab pode ser usado para otimizar funções utilizaremos
um de seus programas de demonstração denominado demopt1. O programa demopt1
demonstra a otimização da seguinte função:
y ( x1 , x2 ) = 100( x2 − x12 ) 2 + (1 − x1 ) 2 , (1.21)
conhecida como função de Rosenbrock utilizando quatro técnicas diferentes.

No Matlab podemos visualizar a superfície definida pela função acima com um único
comando:
> ezsurfc ('100*(x1-x2^2)^2+(1-x1)^2',[-2, 2],[-2,2] )

18

Alternativamente, podemos utilizar a seguinte sintaxe menos direta:

1 x1=-2:0.01:2;
2 x2=-2:0.01:2;
3 [sx1, sx2] =meshgrid (x1,x2);

As instruções acima geram matrizes que contém o produto cartesiano dos vetores x1 e
x2, assim se digitarmos

> [sx1(10,23) sx2(10,23)]

ans =
-1.7800 -1.9100

Veremos um par específico de valores.
A função de Rosenbrock pode ser calculada de duas formas:

> Y= 100*(sx1-sx2.^2).^2 +(1-sx1).^2;
> size(Y)

ans =
401 401

onde utilizamos ".^ " com um ponto antes da operação para elevarmos cada componente
das matrizes X1 e X2, sem "." teríamos calculado um produto matricial. Note que a
resposta é uma discretização da superfície com 401 por 401 pontos.

Para exemplificar o cálculo com e sem ".":

>A=[0 1; 1 0]
A=
0 1
1 0

Um produto matricial será:

> A^2
ans =
1 0
0 1
ou
> A*A
ans =
1 0
0 1

19

Componente a componente teremos
> A.^2
ans =
0 1
1 0

Uma outra forma de avaliarmos a função de Rosenbrock é utilizarmos diretamente a
função do Netlab chamada rosen:
> Y1=rosen([sx1(:),sx2(:)]);

Esta operação retorna um vetor com 401 x 401 valores:
> size(Y1)
ans =
160801 1

Este vetor pode então ser convertido em uma matrz com as dimensões apropriadas
utilizando:

> Y1=reshape(Y1,length(x1),length(x2));

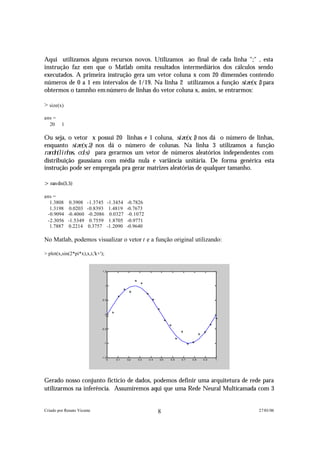
Esta instrução converte um vetor em uma matriz com o número de linhas igual ao
número de dimensões do vetor x1 (length(x1)) e o número de colunas igual ao número
de dimensões do vetor x2 (length(x2)). A matriz é preenchida coluna a coluna conforme o
exemplo a seguir:

>A=[1 2 3 4 5 6 7 8 9 10 11 12];
>A=reshape(A,4,3)
A=
1 5 9
2 6 10
3 7 11
4 8 12

Para plotarmos a superfície podemos utilizar a seguinte instrução :
>surf(x1,x2,Y)

Podemos também plotar curvas de nível da superfície:
> l=-1:6;
>v=2.^l;
>contour(x1,x2,Y,v)

20

Os mínimos da função são (-1,1) e (1,-1).

As funções de otimização do Netlab utilizam a seguinte sintaxe:
> [x, options, errlog, pointlog] = nome ('function', x, options, 'grad');

São quatro as funções de otimização: quasinew (Quase-Newton), conjgrad (gradiente
conjugado), scg (gradiente conjugado escalado) e graddesc (Gradient Descent). Os
argumentos das funções são, respectivamente: a função que se quer otimizar 'function', o
ponto inicial x, o vetor de opções de otimização options e o gradiente da função que se
quer otimizar 'grad'.

As saídas destas funções são, respectivamente: o resultado da otimização x, o vetor de
opcções de otimização atualizado após o processo options, os valores de erro após cada
ciclo errlog e a trajetória percorrida no espaço dos parâmetros pointlog.

O vetor options contém parâmetros para operação da rotina de otimização e parâmetros
específicos para cada algoritmo:

options(1) : 1 para mostrar na tela os valores de erro, 0 para exibir apenas mensagens de
aviso e -1 para não exibir nada;

options(2): Valor da precisão absoluta requerida para encerrar o processo de otimização.
Se xt +1 − xt < options (2) então esta condição é satisfeita.

options(3): Valor da precisão requerida na função otimizada. Se
function(xt +1 ) − function(xt ) < options(3) então a condição é satisfeita. Se esta e a
condição acima forem satisfeitas a otimização é encerrada.

21

options (7): 1 se uma busca em linha é utilizada para minimização na direção do
gradiente, 0 (default) se cada passo é dado na direção do negativo do gradiente com um
learning rate definido por options(18).

options(9): 1 para que a função verifique o gradiente informado 'grad' contra a função
'function'.

options(10): registra o número total de avaliações de 'function'.

options(11): registra o número total de avaliações de 'grad'.

options(14): número máximo de iterações.

options(18): learning rate. (default=0.01).

Gradient Descent

O método de gradient descent consiste na escolha do negativo do gradiente da função
erro como direção para cada passo de otimização, o tamnho de cada passo é definido
por uma learning rate η assim:
w t +1 = w t − η∇E (w t ) (1.22)
Os pontos fixos do algoritmo em (1.22) coincidem com os extremos da função erro, no
entanto nada garante que ocorra convergência para estes pontos fixos. Analisemos a
convergência do gradient descent em torno de um ponto fixo w* .

O gradiente da função erro em torno de um ponto fixo pode ser aproximado (utilizando
uma série de Taylor) por :

∇E (w ) ≅ ∇∇E (w* ) (w − w* ) , (1.23)

onde H = ∇∇E é o Hessiano da função erro.

Sejam λ j os autovalores do Hessiano e u j seus autovetores assim:
Hu j = λ j u j (1.24)
*
Expandindo w-w na base destes autovetores teremos:
∇E ≅ ∑ α j λ j u j e (1.25)
j

(w t +1 − w* ) − (w t − w* ) = ∑ (α t +1 − α t )u j (1.26)
j

Utilizando (1.22) podemos escrever uma dinâmica para as componentes do caminho
traçado no espaço dos parâmetros na direção de cada autovetor do Hessiano:
∆α j = −ηλ jα j (1.27)

22

A dinâmica ao redor do ponto fixo será :
α j ,t +1 = (1 − ηλ j )α j ,t (1.28)
Considerando learning rate η fixa, para n passos teremos:
α j ,t + n = (1 − ηλ j ) n α j ,t (1.29)
De (1.29) fica patente que uma condição necessária para que haja convergência de todas
as componentes para o ponto fixo α j = 0 quando n → ∞ é
1 − ηλ j < 1 . (1.30)
Esta condição obriga que a learning rate η respeite :
2
η< , (1.31)
λmax
onde λmax é o maior autovalor do Hessiano. Note que quanto maior o produto da
learning rate pelo autovalor, menor é o fator multiplicador em (1.29) e, por
conseqüência, mais rápida é a convergência. Quando o Hessiano possuir um espectro de
autovalores amplo (o que ocorre freqüentemente) as várias direções apresentarão tempos
de convergência bem diferentes. O processo total de convergência é dominado pela
direção com convergência mais lenta, ou seja, a direção com menor autovalor. A
convergência será então dominada por:
λ
(1 − 2 min ) . (1.32)
λmax
Se na vizinhança de um ponto fixo o Hessiano apresentar autovalores muito diferentes
, ou seja, a superfície de erro apresentar curvas de nível elipsoidais bastante alongadas, a
convergência do algoritmo será muito lenta.

Em geral gradient descent é bastante ineficiente sendo de pouco interesse prático. Apesar
disso este algoritmo recebeu bastante atenção do meio acadêmico devido à facilidade de
análise utilizando técnicas exatas. Várias formas de melhorar seu desempenho foram
propostas entre elas: adição de um termo de "momento", redução do número de passos
necessários para convergência pela utilização de um esquema para minimização
unidimensional e implementação de learning rates variando com o tempo.

O termo de momento é como segue:
w t +1 = w t − η∇E (w t ) + µ (w t − w t −1 ) , (1.33)
com 0 ≤ µ ≤ 1 .

Este termo tem o mesmo sinal da última variação, assim, se uma componente foi
reduzida ela continuará sendo reduzida. Em geral isto será uma vantagem em trechos da
superfície de erro em forma de vale, com pouca curvatura na direção do mínimo e muita
curvatura em uma outra direção qualquer como ilustrado a seguir.

23

>ezsurfc ('10*x1^2+x2',[-1, 1],[0,10] )

O gradiente da função acima é ∇E = (10 x1 ,1) , assim, se iniciarmos a otimização fora do
eixo x1 = 0 teremos fortes oscilações em decorrência da grande curvatura de uma das
direções:

O termo de momento neste caso adicionará uma certa inércia à direção (0,1)
aumentando a taxa de convergência.

Uma outra forma de reduzirmos o número de passos necessários para convergência é a
redução do número de dimensões do problema apenas à direção do gradiente pela
introdução de um algoritmo de otimização unidimensional a cada passo de otimização.

24

Nesta variante a cada passo encontramos a amplitude do deslocamento na direção do
gradiente , assim:
w t +1 = w t − λ *∇E (w t ) , (1.34)
onde λ * é definido como o mínimo de:
E (λ ) = E (w t − λ∇E ( w t )) . (1.35)
De forma equivalente, escolhemos λ de forma a termos:

dE (λ )
= −∇E (w t +1 ) ⋅∇E (w t ) = 0 , (1.36)
dλ
ou seja, gradientes sucessivos ortogonais. A minimização unidimensional em (1.35) pode
ser realizada utilizando uma busca linear. Utilizando esta forma é possível aumentar
consideravelmente a velocidade de convergência do gradient descent. O incoveniente deste
algoritmo está na condição (1.36) que força movimentos em zig-zag no espaço de
parâmetros.

Neste ponto, vale a pena discutirmos um pouco algoritmos de busca linear. O Netlab
utiliza um algoritmo proposto por Brent1 bastante eficiente e robusto que não utiliza o
gradiente unidimensional da função na otimização . O algoritmo de Brent consiste em:

1. Encontrar 3 pontos a<b<c, tais que E(b)<E(a) e E(b)<E(a) .
2. Ajustar uma parábola passando pelos pontos a,b e c.
3. Minimizando a parábola para encontrar d.
4. Repetindo o processo para pontos d e escolhendo entre a,b,c os dois com menor
erro.

Em Netlab uma busca linear é implementada pela função a seguir:

> [x, options] = linemin(f, pt, dir, fpt, options);

Onde f é a função a ser minimizada, pt é o ponto inicial, dir é a direção que define a
linha de busca, fpt é o valor da função no ponto de início e options é o vetor de opções de
otimização. O ponto de mínimo é dado por pt+x.*dir.

Como exemplo apresentamos a seguir otimização da função de Rosenbrock empregando
Gradient Descent seguirá os seguintes passos:

1 options = foptions;

Para importar configurações padrão para o otimizador.

1
Brent, R. 1973, Algorithms for Minimization without Derivatives. Englewood Cliffs, NJ: Prentice-Hall.

25

2 options(1) = -1;
3 options(3) = 1e-8;
4 options(7)=1;
5 options(14) = 100;

Nada é exibido na tela , a precisão requerida para as variações na função otimizada é de 10-
8
, a otimização empregará a variante com busca linear e o número total de iterações é
fixado em 100. O vetor options inicia o processo na seguinte configuração:

>options(1)
ans =
-1
>options(2)
ans =
1.0000e-004
>options(3)
ans =
1.0000e-008
>options(9)
ans =
0
>options(10)
ans =
0
>options(11)
ans =
0
>options(14)
ans =
100

Assim a otimização deve encerrar quando as precisões fixadas forem atingidas ou quando o
número de iterações chegar a 100. Para vermos todas as outras opções disponíveis basta
utilizarmos o comando:

> help graddesc
GRADDESC Gradient descent optimization.

Description
[X, OPTIONS, FLOG, POINTLOG] = GRADDESC(F, X, OPTIONS, GRADF) uses
batch gradient descent to find a local minimum of the function F(X)
whose gradient is given by GRADF(X). A log of the function values
after each cycle is (optionally) returned in ERRLOG, and a log of the
points visited is (optionally) returned in POINTLOG.

Note that X is a row vector and F returns a scalar value. The point
at which F has a local minimum is returned as X. The function value
at that point is returned in OPTIONS(8).

GRADDESC(F, X, OPTIONS, GRADF, P1, P2, ...) allows additional

26

arguments to be passed to F() and GRADF().

The optional parameters have the following interpretations.

OPTIONS(1) is set to 1 to display error values; also logs error
values in the return argument ERRLOG, and the points visited in the
return argument POINTSLOG. If OPTIONS(1) is set to 0, then only
warning messages are displayed. If OPTIONS(1) is -1, then nothing is
displayed.

OPTIONS(2) is the absolute precision required for the value of X at
the solution. If the absolute difference between the values of X
between two successive steps is less than OPTIONS(2), then this
condition is satisfied.

OPTIONS(3) is a measure of the precision required of the objective
function at the solution. If the absolute difference between the
objective function values between two successive steps is less than
OPTIONS(3), then this condition is satisfied. Both this and the
previous condition must be satisfied for termination.

OPTIONS(7) determines the line minimisation method used. If it is
set to 1 then a line minimiser is used (in the direction of the
negative gradient). If it is 0 (the default), then each parameter
update is a fixed multiple (the learning rate) of the negative
gradient added to a fixed multiple (the momentum) of the previous
parameter update.

OPTIONS(9) should be set to 1 to check the user defined gradient
function GRADF with GRADCHEK. This is carried out at the initial
parameter vector X.

OPTIONS(10) returns the total number of function evaluations
(including those in any line searches).

OPTIONS(11) returns the total number of gradient evaluations.

OPTIONS(14) is the maximum number of iterations; default 100.

OPTIONS(15) is the precision in parameter space of the line search;
default FOPTIONS(2).

OPTIONS(17) is the momentum; default 0.5. It should be scaled by the
inverse of the number of data points.

OPTIONS(18) is the learning rate; default 0.01. It should be scaled
by the inverse of the number of data points.

See also
CONJGRAD, LINEMIN, OLGD, MINBRACK, QUASINEW, SCG

Definimos o ponto inicial como:

5 x = [-2,3];

27

A otimização propriamente dita pode ser implementada em uma linha :

6 [x,options,errgd,trajgd]=graddesc('rosen',x,options,'rosegrad');

O resultado final da otimização está longe do valor correto:
>x
x=
-0.5424 0.2886

A figura a seguir ilustra a trajetória percorrida durante o processo de otimização:

>a = -1.5:.02:1.5;
>b = -0.5:.02:2.1;
>[A, B] = meshgrid(a, b);
> Z = rosen([A(:), B(:)]);
> Z = reshape(Z, length(b), length(a));
> l = -10:6;
> v=2.^l;
> contour(a, b, Z, v);
> hold on;

> plot(trajgd(:,1), trajgd(:,2), 'b-', 'MarkerSize', 6)
> title('Gradient Descent')

Exercícios

(1) Repita a otimização acima para o gradient descent sem termo de momento com
os seguites valores para learning rate η = 0.001,0.01, 0.5 . Construa o gráfico
acima em cada um dos casos. Repita os experimentos adicionando momentos
µ = 0.1, 0.5 .

28

29

Gradiente Conjugado

Como vimos anteriormente o método de gradient descent consiste na escolha do
negativo do gradiente da função erro como direção para cada passo de otimização. Em
sua versão mais eficiente o tamanho de cada passo é definido por uma busca linear,
assim:
w t +1 = w t − λ *∇E (w t ) ,
onde
λ * = arg min E (w t − λ∇t E ) . (2.1)
Esta escolha tem a incoveniência de induzir uma trajetória em zig-zag no espaço dos
parâmetros já que:
dE
= 0 ⇒ ∇E (w t +1 ) ⋅ ∇E (w t ) = 0 , (2.2)
d λ λ =λ *
o que implica que duas direções de otimização consecutivas são sempre ortogonais. A
condição (2.1) garante que a função seja minimizada na direção do gradiente ∇t E , no
entanto o passo seguinte na direção do gradiente ∇t +1 E não garante que (2.2) continue
sendo verdade, assim cada passo pode destruir parte do trabalho de otimização do passo
anterior. Uma maneira de solucionar este problema é impor que a nova direção dt+1 de
otimização seja tal que o gradiente no novo ponto no espaço dos parâmetros não tenha
componentes na direção dt do último passo de otimização, assim:
∇E (w t+1 + λ d t+1 ) ⋅ d t = 0 . (2.3)
Expandindo o gradiente acima ao redor de wt+1 teremos:
(∇E (w t +1 ) + Hdt +1 ) ⋅ dt ≅ 0 , (2.4)
onde H é o Hessiano e por construção teremos que:
dt ⋅ Hdt +1 ≅ 0 . (2.5)
As direções acima são mutuamente conjugadas . Vetores mutuamente conjugados formam
uma base ortogonal com métrica definida pelo Hessiano H. Suponhamos agora que
iniciamos o processo de otimização no ponto w1 do espaço dos parâmetros.
Suponhamos que w* seja o mínimo da função erro E. A correção necessária para
atingirmos o mínimo da função erro pode ser expandida em uma base de vetores
mutuamente conjugados:
N
w * − w1 = ∑ α i d i , (2.6)
i =1

onde N é a dimensão do espaço de parâmetros. Se definirmos
j −1
w j = w1 + ∑ α i d i , (2.7)
i =1

teremos a correção no componente j do vetor de parâmetros, alternativamente
w j +1 = w j + α j d j (2.8)
expressa como cada componente do vetor de parâmetros é corrigida a partir da
componente anterior. Assim a otimização utilizando gradientes conjugados ocorre por

29

otimização de uma componente por vez. Desta forma se calcularmos exatamente as
direções conjugadas em cada passo precisaremo de exatos N passos para otimização. Para
superfícies quadráticas apenas precisamos calcular a Hessiana (segundas derivadas) uma
única vez. As direções conjugadas são obtidas simplesmente resolvendo um problema de
autovalores para H pois :

d k ⋅ Hd j = λ j d k ⋅ d j = λ jδ jk , (2.9)

Para superfícies genéricas o problema se torna mais complicado pois a Hessiana muda
conforme a posição no espaço dos parâmetros e seria necessário recalcular a Hessiana e
resolver o problema de autovalores acima para cada ponto. Para entendermos como
podemos utilizar gradientes conjugados de forma prática, começamos por analisar o caso
mais simples de uma superfície quadrática.

Suponhamos que a superfície de erro que queremos minimizar tenha a seguinte forma:
1
E (w ) = ω ⋅ w + w ⋅ Hw . (2.10)
2
O gradiente desta função erro no ponto w será:
∇E (w ) = ω + Hw . (2.11)
O ponto de mínimo será:
ω + Hw * = 0 . (2.12)
Agora, utilizando (2.6) teremos:
(2.13)
 
d j ⋅ H ( w * − w1 ) = d j ⋅ H  ∑ α i d i  ,
N
(2.14)
 i =1 
onde dj são direções conjugadas.
Utilizando (2.12):
N
−d j ⋅ ω − d j ⋅ Hw1 = ∑ α i d j ⋅ H di = α j d j ⋅ H d j . (2.15)
i =1

Assim encontramos a correção necessária em cada uma das direções conjugadas:
d ⋅ (ω + Hw1 )
αj = − j . (2.16)
dj ⋅H dj
Utilizando (2.7) teremos
j −1
d j ⋅ Hw j = d j ⋅ Hw1 + ∑ α i d j ⋅ Hdi = d j ⋅ Hw1 e (2.17)
i =1 !#"
" $
0

d j ⋅ (ω + Hw j ) d j ⋅∇E (w j )
αj = − . =− (2.18)
dj ⋅H dj dj ⋅H dj
Calculadas as correções em cada uma das direções conjugadas temos que encontrar uma
forma de encontrarmos as próprias direções que seja mais eficiente do que o cálculo de
Hessianas e a solução de problemas de autovalor. Uma maneira prática consiste em

30

adotarmos como primeira direção o negativo do gradiente no ponto de início
d1 = −∇E (w1 ) . A seguir construímos cada uma das direções iterativamente:
d j +1 = −∇E (w j +1 ) + β j d j (2.19)
Empregando a condição para direções conjugadas teremos:
d j +1 ⋅ Hd j = −∇E (w j +1 ) ⋅ Hd j + β j d j ⋅ Hd j = 0 e (2.20)
−∇E (w j +1 ) ⋅ Hd j
βj =
d j ⋅ Hd j
Se assumirmos uma aproximação quadrática em torno de cada ponto do espaço
poderemos empregar (2.20) como algoritmo para qualquer superfície. Nesta aproximação
podemos escrever:
∇E (w j +1 ) − ∇E (w j ) = Hw j +1 − Hw j = α j Hd j (2.21)
e por conseqüência:

−∇E (w j +1 ) ⋅ ∇E (w j +1 ) − ∇E (w j ) 
 
βj = (2.22)
d j ⋅ ∇E (w j +1 ) − ∇E (w j ) 
 
conhecida como equação de Hesteness-Stiefel1. Com algum trabalho de álgebra é possível
mostrar que :
∇E (w j ) ⋅ d k = 0, j ≠ k

Empregando (2.19) teremos também que
d j ⋅∇E (w j ) = −∇E (w j ) ⋅∇E (w j ) . (2.23)
Substituindo em (2.22) encontramos a equação de Polak-Ribiere 2:
(2.24)
−∇E (w j +1 ) ⋅ ∇E (w j +1 ) − ∇E (w j ) 
 
βj = . (2.25)
∇E (w j ) ⋅∇E (w j )
Note que não é necessário calcular o Hessiano para avaliarmos as direções conjugadas, no
entanto precisamos desta avaliação para calcularmos o tamanho do passo α j (vide
expressão (2.18) ). Para evitarmos o cálculo do Hessiano, muito caro para um número
muito grande de dimensões, podemos utilizar uma busca linear na direção conjugada do
momento. Assim chegamos a uma descrição completa do algoritmo de gradientes
conjugados:
1. Escolha um ponto inicial no espaço dos parâmetros w1 ;
2. Calcule o gradiente no ponto inicial e faça a primeira direção de otimização ser
d1 = −∇E (w1 ) ;
3. Para descobrir a amplitude do passo na direção d1, utilize uma busca linear
encontrando α1 = arg min E (w j + α d1 ) ;

1
Hestenes, M.R. e E. Stiefel (1952). Methods of conjugate gradients for solving linear systems. Journal of
Research of the National Bureau of Standards 49 (6), 409-436.
2
Polak, E. (1971). Computational Methods in optimization: A unified Approach. New York: Academic Press.

31

4. Calcule w 2 = w1 + α1d1 ;
5. Pare se os critérios de convergência foram satisfeitos
6. Calcule ∇E (w 2 ) ;
7. A nova direção é dada por d 2 = −∇E (w 2 ) + β1d1 , com β1 definido pela relação de
Polak-Ribiere.
8. Vá para o passo 3 para o novo d.

Utilizemos agora a implementação em Netlab do algoritmo de gradiente conjugado para
otimizarmos novamente a função de Rosenbrock. Começamos por verificar as opções
de otimização disponíveis para a função conjgrad:

> help conjgrad

CONJGRAD Conjugate gradients optimization.

Description
[X, OPTIONS, FLOG, POINTLOG] = CONJGRAD(F, X, OPTIONS, GRADF) uses a
conjugate gradients algorithm to find the minimum of the function
F(X) whose gradient is given by GRADF(X). Here X is a row vector and
F returns a scalar value. The point at which F has a local minimum
is returned as X. The function value at that point is returned in
OPTIONS(8). A log of the function values after each cycle is
(optionally) returned in FLOG, and a log of the points visited is
(optionally) returned in POINTLOG.

CONJGRAD(F, X, OPTIONS, GRADF, P1, P2, ...) allows additional


displayed.

OPTIONS(2) is a measure of the absolute precision required for the
value of X at the solution. If the absolute difference between the
values of X between two successive steps is less than OPTIONS(2),
then this condition is satisfied.


OPTIONS(9) is set to 1 to check the user defined gradient function.


32



default 1E-4.

See also
GRADDESC, LINEMIN, MINBRACK, QUASINEW, SCG

Primeiro inicializamos as opções de otimização carregando as opções de default com:
> options=foptions
options =
Columns 1 through 8
0 0.0001 0.0001 0.0000 0 0 0 0
Columns 9 through 16
0 0 0 0 0 0 0 0.0000
0.1000 0

Ajustamos então algumas destas opções:
>options(1)=-1;
Para não mostrarmos em tela a trajetória de otimização.

>options(3)=1e-8;
Se em dois passos consecutivos a função erro diferir em menos de 1e-8 e se o vetor de
parâmetros diferir em menos de 1e-2 (options(2) ) a otimização deverá ser encerrada.

>options(14)=100;
A otimização deverá parar se o número de iterações atingir 100.

Agora definimos o ponto inicial :
> x=[-2 3];
A otimização é realizada em uma única linha:
> [x,options,errgd,trajgd]=conjgrad('rosen',x,options,'rosegrad');

As saídas são
>x
x=
1.0000 1.0000

O ponto ótimo, que neste caso está correto !
>options
options =
Columns 1 through 8
-1.0000 0.0001 0.0000 0.0000 0 0 0 0.0000
0 526.0000 28.0000 0 0 100.0000 0 0.0000
0.1000 0

33

Este vetor nos informa que foram utilizadas 526 avaliações da função minimizada e que o
gradiente desta função foi avaliado 28 vezes ( uma vez a cada iteração).

errgd e trajgd nos informam o valor do erro em cada passo e a trajetória no
espaço dos parâmetros. Para vermos a evolução do erro podemos utilizar
> plot(errgd,'b-o');

É interessante comentar neste ponto que para passarmos funções como argumentos para
rotinas de otimização precisamos criar arquivos .m para a função e para o gradiente da
função.
> edit rosen;

34

>edit rosegrad

35

O Netlab oferece uma função que possibilita a verificação de um gradiente:
>gradchek([-2,3], 'rosen', 'rosegrad');

Checking gradient ...

analytic diffs delta

-806.0000 -806.0000 0.0000
-200.0000 -200.0000 0.0000

Na saída analytic fornece o valor calculado pela função rosegrad , diffs calcula o gradiente
numericamente utilizando a função rosen e delta mostra a diferença entre as duas formas de
cálculo.

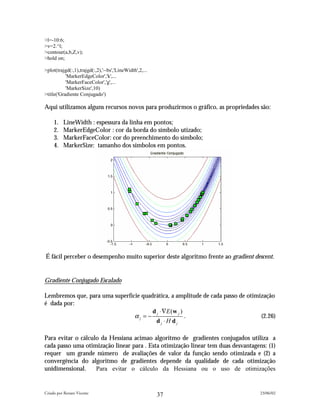
Para visualizarmos a trajetória de otimização repetimos o procedimento utilizado quando
discutimos gradient descent:

>a=-1.5:.02:1.5;
>b=-0.5:.02:2.1;
> [A,B]=meshgrid(a,b);
>Z=rosen([A(:),B(:)]);
>Z=reshape(Z,length(b),length(a));

36

>l=-10:6;
>v=2.^l;
>contour(a,b,Z,v);
>hold on;

>plot(trajgd(:,1),trajgd(:,2),'--bs','LineWidth',2,...
'MarkerEdgeColor','k',...
'MarkerFaceColor','g',...
'MarkerSize',10)
>title('Gradiente Conjugado')

Aqui utilizamos alguns recursos novos para produzirmos o gráfico, as propriedades são:

1. LineWidth : espessura da linha em pontos;
2. MarkerEdgeColor : cor da borda do símbolo utizado;
3. MarkerFaceColor: cor do preenchimento do símbolo;
4. MarkerSize: tamanho dos símbolos em pontos.

É fácil perceber o desempenho muito superior deste algoritmo frente ao gradient descent.

Gradiente Conjugado Escalado

Lembremos que, para uma superfície quadrática, a amplitude de cada passo de otimização
é dada por:
d ⋅∇E (w j )
αj = − j . (2.26)
dj ⋅H dj

Para evitar o cálculo da Hessiana acimao algoritmo de gradientes conjugados utiliza a
cada passo uma otimização linear para . Esta otimização linear tem duas desvantagens: (1)
requer um grande número de avaliações de valor da função sendo otimizada e (2) a
convergência do algoritmo de gradientes depende da qualidade de cada otimização
unidimensional. Para evitar o cálculo da Hessiana ou o uso de otimizações

37

unidimensionais a cada passo Møller3 criou o algoritmo de gradientes conjugados
escalado.

A idéia central do algoritmo é utilizar uma aproximação numérica para o termo
envolvendo a Hessiana em (2.26).

Suponha ε = ε 0 / d j , onde ε 0 é uma quantidade pequena e positiva, observemos que :
∇E (w j + ε d j ) ≈ ∇E (w j ) + ε Hd j , (2.27)
portanto uma aproximação numérica para (2.26) é:
∇E ( w j + ε d j ) − ∇E ( w j )
Hd j ≈ . (2.28)
ε
Esta aproximação funciona se : 1) a função sendo minimizada for quadrática; 2) a
Hessiana for positiva definida. Para superfícies genéricas nada garantirá que a Hessiana é
positiva definida e um passo de otimização utilizando (2.26) poderá aumentar o valor da
função em algumas direções. Para podermos usar a aproximação numérica (2.28) e
minimizar estes efeitos podemos corrigir a equação para:
d j ⋅∇E (w j )
αj = − 2
(2.29)
dj ⋅ H dj +γ j dj
O parâmetro γ regula a escala (daí o nome gradiente conjugado escalado) de cada passo e é
inicializado como γ 1 = 1 . Quanto maior o parâmetro de escala, menor é a amplitude do
passo de otimização. A escala apropriada depende do quanto a função sendo otimizada é
localmente diferente de uma superfície quadrática. Se a função for exatamente quadrática
γ = 0 , se a função for distante de uma função quadrática γ deve aumentar.

Uma medida do grau de similaridade local entre a função e uma superfície quadrática foi
introduzida por Fletcher sendo:
E (w j ) − E (w j + α j d j )
∆j = , (2.30)
E (w j ) − EQ (w j + α j d j )
1
onde EQ (w j + α j d j ) = E (w j ) + α j d j ∇E (w j ) + α 2d j ⋅ Hd j .
j Utilizando (2.26)
2
simplificamos (2.30) e escrevemos:
2  E (w j ) − E (w j + α j d j ) 
∆j =  . (2.31)
α jd j ⋅ d j
Com base neste parâmetro de comparação são feitas escolhas heurísticas para o
parâmetro de escala a cada passo da otimização. As escolhas são as seguintes:
γj
1. Se ∆ j > 0, 75 então γ j +1 = ;
2

3
Møller ,M. (1993). A scaled conjugate gradient algorithm for fast supervised learning. Neural Networks
6(4), 525-533.

38

2. Se 0, 25 < ∆ j < 0, 75 então γ j +1 = γ j ;
3. Se ∆ j < 0, 25 então γ j +1 = 4γ j ;
4. Se ∆ j < 0 então γ j +1 = 4γ j e o passo de otimização não é efetuado;

O algoritmo de gradientes conjugados escalados adquire então a seguinte forma:

1. Escolha um ponto inicial no espaço dos parâmetros w1 ;
2. Inicialize o parâmetro de escala em γ 1 = 1 ;
3. Calcule o gradiente no ponto inicial e faça a primeira direção de otimização ser
d1 = −∇E (w1 ) ;
4. Para descobrir a amplitude do passo na direção d1 utilize (2.28) e (2.29);
5. Calcule w 2 = w1 + α1d1 ;
6. Pare se os critérios de convergência foram satisfeitos;
7. Calcule o parâmetro de comparação ∆ ;
8. Atualize o parâmetro de escala γ de acordo com as condições acima;
9. Calcule ∇E (w 2 ) ;
10. A nova direção é dada por d 2 = −∇E (w 2 ) + β1d1 , com β1 definido pela relação de
Polak-Ribiere;
11. Vá para o passo 3 para o novo d e para o novo parâmetro de escala γ .

A utilização do Netlab para otimização com gradientes conjugados escalados segue
exatamente os mesmos passos que utilizamos para gradientes conjugados.

> options = foptions;
> options(1)=-1;
>options(3)=1e-8;
>options(14)=100;
> x=[-2 3];
> [x,options,errgd,trajgd]=scg('rosen',x,options,'rosegrad');
>x

x=
1.0000 0.9999

> options

options =
-1.0000 0.0001 0.0000 0.0000 0 0 0 0.0000 0 52.0000 78.0000
0 0 100.0000 0 0.0000 0.1000 0

Note que a qualidade do resultado final é ligeiramente inferior àquela obtida com o
gradiente conjugado mas o número de avaliações de função foi reduzido de 526 para 52
ao deixarmos de utilizar otimizações unidimensionais. Para exibirmos a trajetória

39

utilizamos o mesmo código utilizado para o algoritmo de gradiente conjugado, mas
desta vez salvamos um arquivo .m como exibido abaixo:

>trajetória

Neste exemplo o desempenho do gradiente conjugado mostrou-se muito similar, e até
um pouco inferior, ao desempenho do gradiente conjugado simples. Em geral o

40

gradiente conjugado escalado exibe o melhor desempenho, no entanto é interessante
sempre testar cada um dos algoritmos caso a caso.

Método de Newton

O método de Newton se baseia em uma idéia muito simples. Retomemos a expansão de
Taylor para o gradiente em torno de um ponto wj.

∇E ( w ) ≈ ∇E ( w j ) + H ( w − w j ) . (2.32)
Suponhamos agora que w é um mínimo, então:

H (w − w j ) = −∇E (w j ) . (2.33)
Se resolvermos esta equação em w para qualquer wj, então teremos encontrado o
mínimo. A solução para a equação é :
w = w j − H −1∇E (w j ) . (2.34)
Lembrando que (2.34) encontra o mínimo de E , o que equivale a encontrarmos a raiz
f (w ) = ∇E(w ) . Ou seja, em uma dimensão, temos o conhecido método de Newton-
Raphson.
f ( xn )
x = xn − . (2.35)
f ′( xn )
A direção definida por H −1∇E (w j ) é conhecida como direção de Newton e tem como
propriedade principal apontar para um extremo local da função erro.

Quase-Newton

O método de Newton tem uma série de desvantagens que limitam sua utilização prática
em problemas de otimização com muitas dimensões:

1. O algoritmo requer a avaliação e inversão da matriz Hessiana que requerem,
respectivamente, O(W2 N) e O(W3) operações, sendo W o número de parâmetros
e N o número de pontos.

2. Quando a superfície onde a otimização é realizada não é quadrática é necessário
recalcular o Hessiano e seu inverso em cada ponto.

3. Ao redor de alguns pontos o Hessiano pode não ser positivo definido.

Uma alternativa para contornar estes problemas intrínsecos ao método de Newton é
implementar um método que produza uma aproximação positiva definida para a inversa
da matriz Hessiana.

41

Lembremos que na aproximação quadrática:

∇E (w j ) − ∇E (w j −1 ) = H (w j − w j −1 ) (2.36)
Definindo
q j = ∇E (w j ) − ∇E (w j −1 ) e (2.37)
v j = w j − w j −1 (2.38)
v j = Hq j (2.39)
Se quisermos produzir uma aproximação para a inversa da Hessiana podemos exigir que
para cada um dos pontos já excursionados que
G j +1 v i = qi ,1 ≤ i ≤ j (2.40)
Após N passos com vetores linearmente independentes, com N sendo o número de
dimenaões da matriz Hessiana teremos G N = H −1 . Um procedimento para construção
de uma série de matrizes positvas definidas que respeitem (2.40) é conhecido como
algoritmo BFGS (Broyden-Fletcher-Goldfarb-Shanno)4:

 v j ⋅ G j v j  (q j qTj ) (q j vTj ) G j + G j ( v j qTj )
G j +1 = G j + 1 +  − (2.41)
 v j ⋅q j  q j ⋅ v j qj ⋅vj
 
Note que (q j vTj ) significa uma matriz com componentes (q j vTj ) = qi, j vl , j .
il

Em geral a superfície que está sendo otimizada não é quadrática assim a aproximação em
(2.32) tem validade limitada e a amplitude do passo no método quase-Newton deve ser
controlada:
w j +1 = w j + α j G j ∇E (w j ) (2.42)
A amplitude α j do passo de otimização pode ser obtida por uma busca linear, mas isso
só é necessário se o passo de Newton total ( α j =1) aumentar o valor da função erro.

Como fizemos anteriormente, começamos por verificar as instruções no help da função
quasinew:

4
Press et al., Numerical Recipes in C: The Art of Scientific Computing, Cambridge University Press
(disponível gratuitamente em www.nr.com).

42

>help quasinew

QUASINEW Quasi-Newton optimization.

Description
[X, OPTIONS, FLOG, POINTLOG] = QUASINEW(F, X, OPTIONS, GRADF) uses a
quasi-Newton algorithm to find a local minimum of the function F(X)
whose gradient is given by GRADF(X). Here X is a row vector and F
returns a scalar value. The point at which F has a local minimum is
returned as X. The function value at that point is returned in
OPTIONS(8). A log of the function values after each cycle is
(optionally) returned in FLOG, and a log of the points visited is
(optionally) returned in POINTLOG.

QUASINEW(F, X, OPTIONS, GRADF, P1, P2, ...) allows additional


displayed.

OPTIONS(2) is a measure of the absolute precision required for the
value of X at the solution. If the absolute difference between the
values of X between two successive steps is less than OPTIONS(2),
then this condition is satisfied.


OPTIONS(9) should be set to 1 to check the user defined gradient
function.




default 1E-2.

See also
CONJGRAD, GRADDESC, LINEMIN, MINBRACK, SCG

43

> options = foptions;
> options(1)=-1;
>options(3)=1e-8;
>options(14)=100;
> x=[-2 3];
> [x,options,errgd,trajgd]=quasinew('rosen',x,options,'rosegrad');
>x

x=
1.0000 1.0000

Utilizando o método trajetoria.m :

44

Estimação de Densidades de Probabilidade

Simulação e Clustering

No problema típico de simulação em finanças temos dados históricos provenientes de
um determinado processo e desejamos gerar cenários futuros que sejam compatíveis com
o comportamento estatístico observado. Em sua forma mais geral conhecemos uma
seqüência de dados x1 , x2 ,..., xt mais uma seqüência de informações de mercado
z1 , z2 ,..., zt e queremos estimar uma distribuição condicional do futuro em relação ao
passado p ( xt +1 , xt + 2 ,... x1 , z1 ,..., xt , zt ; w) , onde w são parâmetros da distribuição. A
simulação consiste da amostragem de p . Estas simulações são conhecidas como Monte-
Carlo e encontram aplicação importante na avaliação de riscos.

A versão mais simples do problema de estimação de densidades envolve apenas
distribuições conjuntas (não-condicionadas) p ( x; w) . Neste capítulo exemplificaremos
o uso de Netlab na estimação de densidades de probabilidade conjuntas utilizando o
modelo conhecido como Mistura de Gaussianas.

Nosso problema de exemplo será a estimação da densidade conjunta não-condicional de
retornos diários de uma carteira contendo três ações: VALE5, ITAU4 e ELET3.
Representando em um gráfico cerca de 700 dias de séries teremos:

>x=load('retornos.dat');
>plot3(x(:,1),x(:,2),x(:,3),'.');

45

A densidade que observamos é resultado da convolução de um processo com densidades
condicionais de um dia quase-normais, não-estacionário e com grandes mudanças nas
covariâncias. Isso dá origem a uma densidade não-gaussiana.

No problema de clustering queremos separar um conjunto de dados x1 , x2 ,..., xt em
classes C1, C2, ...,Cn para isso modelamos a densidade p ( x; w) como uma mistura de
n
Gaussianas p ( x) = ∑ p (C j ) pgauss ( x C j ) e definimos a qual classe pertence um ponto
j =1

específico x encontrnado a classe que maximiza p (C j x) .

Misturas de Gaussianas

A idéia central por trás da estimação de densidades de porbabilidade utilizando misturas
de normais está na utilização de uma combinação de distribuições simples, no caso
Gaussianas, para modelar distribuições de complexidade arbitrária. É possível mostrar
que, com um número suficientemente grande de densidades gaussianas é possível
representar qualquer densidade 1. Uma mistura de gaussianas é a dada por:

M
p (x) = ∑ P( j ) pgauss (x j ) (3.1)
j =1

Os coeficiente P( j ) são denominados coeficientes de mistura e as densidades pgauss (x j )
são componentes da mistura. Para que (3.1) defina uma densidade de probabilidade as
seguintes condições são necessárias:

M
1. ∑ P( j ) = 1
j =1
0 ≤ P( j ) ≤ 1

2. ∫ dx p gauss (x j ) = 1 ∀j .

Uma representação gráfica para um GMM (Gaussian Mixture Model) é:

∑ P( j ) p(x j)

p(x|j)P(j)

P(j)

1
McLachlan, G.J. e K.E. Basford (1988). Misxture Models: Inference and Applications to Clustering. New
York: Marcel Dekker.

46

Os componentes da mistura têm a seguinte forma genérica:

1  1 
p(x j ) = exp  − (x − µ j ) ⋅ C −1 (x − µ j ) 
j (3.2)
 2 
1/ 2
(2π ) d /2
Cj
As matrizes de covariância Cj podem ter diversas formas que influenciarão o número
de componentes necessário para a representação de uma densidade:

• Esférica: Nesta escolha as covariâncias são descritas por apenas um parâmetro
C j = σ 2 I . O Netlab trás uma demonstração do uso de GMM com componentes
j

esféricos.

>demgmm2

• Diagonal: Cada matriz de covariância é descrita por N parâmetros, onde N é a
dimensão do espaço dos dados, assim Ckl , j = δ klσ k , j . Este caso é exemplificado no
Netlab pela demonstração demgmm3.

47

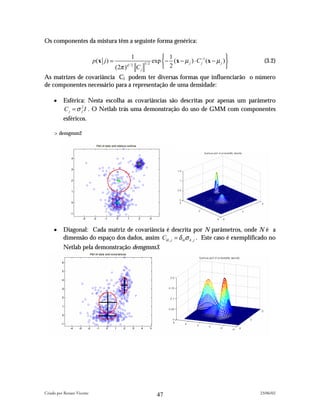
N2 + N
• Completa: A covariância utilizada tem parâmetros , ou seja, Ckl , j = σ kl , j .
2

2
Utilizando demgmm4.

Em Netlab podemos construir um GMM utilizando o comando gmm (dim, comp, covar)
que define uma estrutura com dim dimensões, comp componentes de mistura e
covariância de tipo covar. Se quisermos construir um modelo para a distribuição
conjunta dos retornos das ações descrita acima utilizando 5 componentes com
covariâncias completas, devemos digitar:

> mix= gmm(3,5,'full');

A estrutura definida tem as seguintes componentes:

>mix
mix =
type: 'gmm'
nin: 3
ncentres: 5
covar_type: 'full'
priors: [0.2000 0.2000 0.2000 0.2000 0.2000]
centres: [5x3 double]
covars: [3x3x5 double]
nwts: 65

Os priors são os componentes de mistura e nwts é o número de parâmetros.

A mistura acima precisa ser inicializada, para isso utilizamos o comando gmminit.

48

>help gmminit

GMMINIT Initialises Gaussian mixture model from data

Description
MIX = GMMINIT(MIX, X, OPTIONS) uses a dataset X to initialise the
parameters of a Gaussian mixture model defined by the data structure
MIX. The k-means algorithm is used to determine the centres. The
priors are computed from the proportion of examples belonging to each
cluster. The covariance matrices are calculated as the sample
covariance of the points associated with (i.e. closest to) the
corresponding centres. For a mixture of PPCA model, the PPCA
decomposition is calculated for the points closest to a given centre.
This initialisation can be used as the starting point for training
the model using the EM algorithm.

See also
GMM

>options=foptions;
>mix=gmminit(mix,x,options);
>mix

mix =
type: 'gmm'
nin: 3
ncentres: 5
covar_type: 'full'
priors: [0.0639 0.3083 0.0111 0.4264 0.1903]
nwts: 65

A função gmminit utiliza um algoritmo não-paramétrico denominado K-médias
implementado pela função kmeans do Netlab que consiste dos seguintes passos:

1. Os N dados são são divididos em K grupos S1, S2 e SK com o mesmo número
de componentes;
1
2. São calculadas médias (centros) para cada grupo: µ j = ∑ xn ;
N j n∈S j
3. Calculam-se as distâncias de cada dado em relação a cada um dos centros e
reagrupam-se os dados no grupo de centro mais próximo de forma a
K
minimizar E = ∑ ∑ xn − µ j
2
.
j =1 n∈S j

4. Volta ao passo 2.

Após inicialização o treinamento do GMM é efetuado utilizando um algoritmo de
otimização de verossimilhança denominado EM através da função gmmem.

49

>help gmmem

GMMEM EM algorithm for Gaussian mixture model.

Description
[MIX, OPTIONS, ERRLOG] = GMMEM(MIX, X, OPTIONS) uses the Expectation
Maximization algorithm of Dempster et al. to estimate the parameters
of a Gaussian mixture model defined by a data structure MIX. The
matrix X represents the data whose expectation is maximized, with
each row corresponding to a vector. The optional parameters have
the following interpretations.

values in the return argument ERRLOG. If OPTIONS(1) is set to 0, then
only warning messages are displayed. If OPTIONS(1) is -1, then
nothing is displayed.

OPTIONS(3) is a measure of the absolute precision required of the
error function at the solution. If the change in log likelihood
between two steps of the EM algorithm is less than this value, then
the function terminates.

OPTIONS(5) is set to 1 if a covariance matrix is reset to its
original value when any of its singular values are too small (less
than MIN_COVAR which has the value eps). With the default value of
0 no action is taken.


The optional return value OPTIONS contains the final error value
(i.e. data log likelihood) in OPTIONS(8).

See also
GMM, GMMINIT

Note a opção(5) que tem por objetivo evitar que a covariância colapse sobre um ponto,
o que corresponde a um overfitting dos dados modelados.

>options=foptions;
>options(1)=-1;
> [mix,options,errlog] =gmmem(mix,x,options);
> mix

mix =
type: 'gmm'
nin: 3
ncentres: 5
covar_type: 'full'
priors: [0.0063 0.1210 0.2052 0.2196 0.4479]
nwts: 65

50

Os centros são :
> mix.centres

ans =
0.1779 0.1205 0.2443
-0.0056 0.0001 -0.0091
0.0095 0.0246 0.0130
0.0051 -0.0100 -0.0060
-0.0052 -0.0049 -0.0046

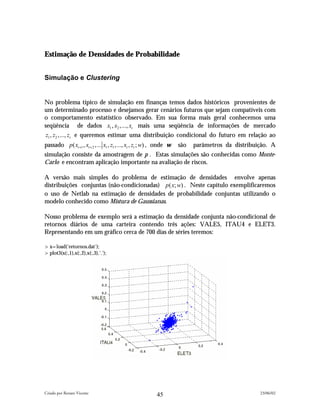
Se quisermos agora simular retornos utilizando nosso modelo recém treinado basta
utilizarmos a função [data,label]=gmmsamp(mix,n), com n sendo o número de amostras,
data sendo os dados amostrados e label a componente geradora.
> [simula,label_sim]=gmmsamp(mix,500);
>plot3(simula(:,1),simula(:,2),simula(:,3),'rs','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g','Mark
erSize',5);

Algoritmo EM (Expectation-Maximization)

A estimação dos parâmetros em um GMM se baseia em um algoritmo conhecido como
EM (Expectation-Maximization) 2. Para encontrarmos os parâmetros mais adequados
para modelar os dados devemos maximizar a função verossimilhança no conjunto de
dados {xn }n =1 :
N

N
L( P, µ , C ) = ∑ ln p ( xn ) , (3.3)
n =1

Esta função de verossimilhança é função dos coeficientes de mistura das médias e das
matrizes de covariância. Para simplificar os cálculos podemos, alternativamente,
minimizar uma função erro definida como:
E = − ln L (3.4)

2
Dempster, A. P., N.M. Laird e D.B. Rubin (1977). Maximum likelihood from incomplete data via the EM
algorithm. journal of the Royal Statistical Society, B 39 (1), 1-38.

51

Se substituirmos a estrutura do GMM em (3.4) teremos:

N
M 
E = − ∑ ln ∑ p ( xn j ) P( j )  (3.5)
n =1  j =1 

Poderiamos utilizar os algoritmos estudados no capítulo anterior para otimizarmos a
funcção erro em (3.5), no entanto, a experiência mostra que , para misturas de gaussianas,
o algoritmo EM converge melhor e mais rápido.

Queremos minimizar (3.5). A cada alteração de parâmetros temos :
N
 p (x ) 
∆E = −∑ ln  t +1 n  (3.6)
n =1  pt ( xn ) 
Se utilizarmos a estrutura da mistura e multiplicarmos o numerador e denominador por
Pt ( j xn ) teremos:
M 
N  ∑ Pt +1 ( j ) pt +1 ( xn j ) P ( j x ) 
∆E = −∑ ln  
j =1 t n
(3.7)
n =1  pt ( xn ) Pt ( j xn ) 
 
 
A manipulação acima teve por objetivo possibilitar o uso da desigualdade de Jensen:

 
Se λ j ≥ 0 e ∑λ j = 1 , então ln  ∑ λ j x j  ≥ ∑ λ j ln( x j ) .
j  j  j
M
Como ∑ P ( j x ) = 1 podemos escrever uma desigualdade baseada em
j =1
t n (3.7):

N M  P ( j ) pt +1 ( xn j ) 
∆E ≤ −∑∑ Pt ( j xn ) ln  t +1  (3.8)
n =1 j =1  Pt ( j x n ) pt ( xn j ) 
 
Na otimização queremos minimizar a função erro E. Isso implica em minimizar ∆E ao
escolher novos parâmetros. Podemos reescrever (3.8) como :

N M N M
Et +1 ≤ Et − ∑∑ Pt ( j xn ) ln  Pt +1 ( j ) pt +1 ( xn j )  + ∑∑ Pt ( j xn ) ln  Pt ( j ) pt ( xn j ) 
    (3.9)
n =1 j =1 n =1 j =1

Note que o último termo acima não depende dos novos parâmetros em t+1 sendo,
portanto, uma constante. Já o segundo termo varia com a escolha de novos parâmetros.
A propriedade interessante de (3.9) é o fato de que qualquer alteração no segundo termo
a direita que reduza o valor da soma dos termos automaticamente implica na redução do
erro no novo passo. Chamemos o segundo termo à esquerda de Q e o terceiro de Q0 ,
teremos:

52

Et +1 ≤ Et + Q( P, µ , C ) + Q0 (3.10)
com
N M
Q( Pt +1 , µt +1 , Ct +1 ) = ∑∑ Pt ( j xn ) ln  Pt +1 ( j ) pt +1 ( xn j ) 
  (3.11)
n =1 j =1

O cálculo de (3.11) é denominado de passo E (Expectation) do algoritmo. Para
otimizarmos o erro precisamos otimizar (3.11), em geral isso requer a utilização de um
dos algoritmos de otimização que discutimos no capítulo anterior. Para o caso de GMMs
é possível obter equações para os parâmetros analíticamente, bastando para isso
substituir (3.2) em (3.11) e calcular as derivadas. Só é necessário tomar cuidado com a
condição de normalização ao otimizar os coeficientes de mistura. Estas condições de
normalização podem ser introduzidas via um multiplicador de Lagrange. A função a ser
otimizada será portanto:

! = Q + λ  P ( j ) − 1
M
Q  ∑ t +1  (3.12)
 j =1 
Calculando as derivada de (3.12) teremos:

N
Pt ( j xn )
λ −∑ =0 (3.13)
n =1 P +1 ( j )
t

Manipulando a expressão acima :
M M N
Pt ( j xn )
λ ∑ Pt +1 ( j ) − ∑ Pt +1 ( j )∑ =0 (3.14)
j =1 j =1 n =1 P +1 ( j )
t

Assim λ = N . Calculando todas as derivadas chegamos ao passo M (Maximization) do
algoritmo :

N
1
Pt +1 ( j ) =
N
∑ P( j x )
n =1
t n (3.15)
N

∑ x P( j x )n t n
µt +1 ( j ) = n =1
N
(3.16)
∑P( j x )
n =1
t n

N

∑ P ( j x )( x
t n n − µt +1 ( j ))( xn − µt +1 ( j ))T
Ct +1 ( j ) = n =1
N
(3.17)
∑ P( j x )
n =1
t n

53

O Netlab possui uma demonstração do algoritmo EM entitulada demgmm1. Nesta
demosntração dados de exemplo são gerados a partir de duas distribuições gaussianas com
covariância esférica.

Um GMM com duas componentes é inicializado .

Aplica-se o passo E e registra-se a verossimilhança de cada ponto em uma escala de cores
do vermelho ao azul, dependendo de qual das duas componentes tem maior contribuição.

54

A seguir os parâmetros são atualizados no passo M.

Os passos E e M são então alternados até que haja convergência .

55

Exercício

(1) Separe os dados em retornos.dat em dois grupos. O primeiro contendo 600
pontos o segundo o restante. Modele os retornos diários com GMMs com
números de componentes M=1,...,10 utilizando o primeiro conjunto. Avalie a
N
função de log-verossimilhança ln L = ∑ ln p ( xn ) no segundo conjunto (de teste)
n =1

para cada M. Construa um gráfico da log-verossimilhança contra o número de
componentes. Qual é o número de componentes mais adequado ?

Sugestão: Utilize a função gmmprob no cálculo da log-verossimilhança.

56

Redes Neurais Camada Única

Perceptron Linear: Regressão Linear

O perceptron linear implementa a seguinte família de funções:

M
y (x, w ) = ∑ w j x j + w0 (3.1)
j =1
A representação gráfica do percéptron é como segue:

w

x
Dado um conjunto de dados D = {(x n , tn )}n =1 , o treinamento do perceptron envolve a
N

maximização da verossimilhança de D:
N
L(w ) = ∏ p (t j x j ) , (3.2)
j =1

onde p(t j x j ) é a densidade condicional que deve descrever o processo gerador dos dados
D. Supondo que os dados são gerados por funções na família (3.1) corrompidas por ruído
teremos:
t j = y (x j w ) + ε j . (3.3)

Conforme procedimento dos capítulos anteriores introduzimos uma função erro:
E (w ) = − ln L(w )
N
(3.4)
= −∑ ln p (t j x j )
j =1

Com um modelo de ruído gaussiano teremos:
1  (t − y (x w )) 2 
p(t w ) = p(t − y (x w )) = exp  −  (3.5)
2πσ  2σ 2 

57

Substituindo (3.5) em (3.4) e ignorando os termos que não dependem dos parâmetros w
teremos:
1 N
E (w ) = ∑  y ( x j w ) − t j  .
2
(3.6)
2 j =1  
A minimização de (3.6) é conhecida como método dos mínimos quadrados.

Para efetuarmos a otimização de (3.6) precisamos conhecer seu gradiente , o cálculo é
simples:
∂E N
= ∑  y j (w ) − t j xn, j (3.7)
∂wn j =1  
Se introduzirmos δ j = y j (w ) − t j teremos:
∂E N
= ∑ δ j xn , j , (3.8)
∂wn j =1
onde j denota cada um dos exemplos e n cada um dos parâmetros, para o limiar w0 temos
∂E N
= ∑δ j . (3.9)
∂w0 j =1
O gradiente pode ser avaliado em duas etapas:
1. Cáculo das contribuições δ j = y j (w ) − t j de cada dado ao erro quando os
parâmetros são w ;
2. Cálculo do gradiente conforme (3.8) e (3.9) .

Em Netlab o treinamento de um perceptron linear pode ser feito utilizando qualquer um
dos métodos de otimização já vistos.

Como exemplo de aplicação utilizaremos retornos do índice BOVESPA e da
Companhia Vale do Rio Doce (VALE5). Suponhamos que os retornos da VALE5
possam ser representados como (CAPM):
RVALE = β RIBOV + ε , (3.10)
onde ε é um termo de ruído com média nula.
Poderíamos eventualmente adicionar mais fatores ao modelo:
RVALE = β1 RIBOV + β 2 x2 + ... + β n xn + ε , (3.11)
assim teríamos uma regressão linear multifatorial, ou, um perceptron linear.

58

Voltando ao exemplo, abaixo representamos os retornos acima.

No Netlab redes de camada única são identificadas como Generalized Linear Models
(GLM). A função para criação de uma GLM é, como não poderia deixar de ser, glm .
Para nosso problema exemplo é:

> net=glm(1,1,'linear');
> net

net =
type: 'glm'
nin: 1
nout: 1
nwts: 2
actfn: 'linear'
w1: 0.0886
b1: 0.2034

A sintaxe de glm é net=glm (nr. entradas, nr. saídas, 'função de saída'). As funções de
saída são:

1. 'linear': y ( x) = x ;
1
2. 'logistic': y ( x) = ;
1 + e− x
x
ej
3. softmax: y j = .
∑ e xk
k

59

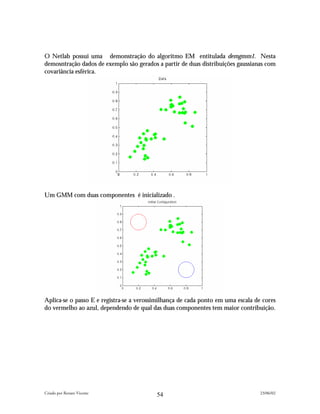
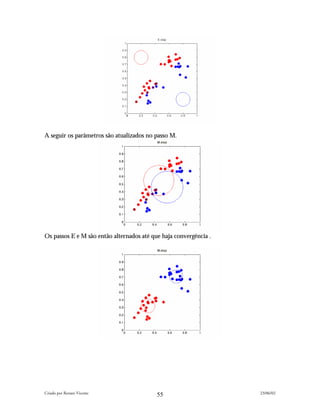
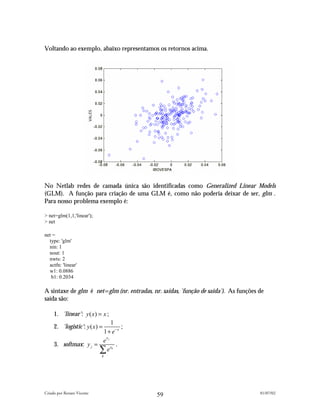
A função 'logistic' é utilizada nas regressões logísticas comuns em sistemas de aprovação
automática de crédito. Já a função softmax é utilizada em classificações que envolvem
várias classes diferentes (por ex.: rating de crédito).

Dada a estrutura net com parâmetro w, a função erro é avaliada pela função glmerr e o
gradiente pela função glmgrad, em geral é convenção do Netlab representar o erro e o
gradiente da seguinte forma:

<tipo_de_rede>err(net,x,t) , para o erro ;
<tipo_de_rede>grad(net,x,t), para o gradiente.

Desta foram podemos usar sem maiores dificuldades a função genérica para treinamento
de redes. Primeiro carregamos os dados, o arquivo beta.dat contém duas colunas , a
primeira com retornos do Ibovespa e a segunda com retornos vale5 :

>load('beta.dat');
>ibov=beta(:,1);
>vale=beta(:,2);

Então, inicializamos o otimizador e chamamos netopt
> options=foptions;
> [net,options]=netopt(net,options,ibov,vale,'scg');
O resultado é:
>net

net =
type: 'glm'
nin: 1
nout: 1
nwts: 2
actfn: 'linear'
w1: 0.5864
b1: -9.8947e-004

60

Ou seja, temos que : RVALE = 0,586 RIBOV − 10−3 + ε . A rede treinada pode ser utilizada
através da função glmfwd. Assim:

> plot(ibov,vale,'o');
> hold;
> x=-0.08:0.001:0.08;
> valemodel=glmfwd(net,x');
> plot(x,valemodel);

Para avaliarmos a qualidade do ajuste podemos recorrer à função glmerr fora do conjunto
de treinamento. Dentro do conjunto de treinamento temos:
> e=glmerr(net,ibov,vale)
e=
0.0329

Que equivale a uma verossimilhança de
>L=exp(-e)

L=
0.9676

Exercício

(a) Prepare um arquivo ASCII com retornos do Ibovespa, Dow Jones, Nasdaq,
R$/dólar e quaisquer outras variáveis que achar necessário. Carregue os dados em
Matlab e implemente em Netlab uma regressão linear multifatorial.

(b) Separe o conjunto em treinamento (80%) e teste (20%). Calcule a verossimilhança
do modelo no conjunto de teste considerando modelos que contenham: i) apenas um fator
para ibovespa, ii) fatores para ibovespa e dólar, iii) todos os fatores. Qual é o melhor
modelo ?

61

Redes Neurais Multicamada

Perceptron Multicamada: Regressão Não-Linear

Redes multicamada (MLP) com uma camada escondida implementam a seguinte família
de funções :

M  N  
y (x, W ) = g  ∑ wm 0ϕ m  ∑ w jm x j + w0  + w0 
out
(4.1)
 m=1
  j =1  

A representação gráfica de uma MLP é como segue:

wout

w

x

A função de transferência da camada de saída é g . Para a camada escondida as funções de
transferência são ϕ1 ,..., ϕ M . Note que a rede para (4.1) possui M entradas e n neurônios
na camada escondida.

Se escolhermos g ( z) = z e ϕm como sendo funções sigmoidais contínuas
( ϕ ( z ) = tanh( z ) ou ϕ ( z ) = erf ( z ) ), (4.1) pode representar uma função f : ! N ! !
com precisão arbitrária !( M ) " f (x) # yM (x; W ) , sendo que !( M ) %% % 0 1. Assim,
M !$
!
se os dados observados consistirem de uma função multidimensional desconhecida
corrompida por um nível moderado de ruído uma MLP com um número apropriado de
unidades na camada escondida será capaz de extrair esta dependência funcional.

Seja um conjunto de observações D = {(x ( n ) , t ( n ) )}n =1 , suponhamos que
P

t ( n ) " f (x ( n ) ) & !n . (4.2)

1
Hornik, K. (1991). Approximation capabilities of multilayer feedforward networks. Neural Networks 4
(2), 251-257.

62

Com !n " ' e !n !q "0 ,
n( q
onde ' é uma densidade de probabilidade arbitrária . Ao

treinarmos uma rede neural utilizando o conjunto D de dados procuramos encontrar
parâmetros W que tornem y(x;W) o mais próximo de f possível dado um modelo para
o ruído definido pela densidade ' . De forma equivalente, desejamos encontrar
parâmetros para um modelo de densidade condicional p (t x; W ) . Parâmetros
adequados podem ser encontrados, como procedemos anteriormente, maximizando a
função verossimilhança sobre o conjunto D definida por:
P
L( W) = ∏ p (t ( n ) x( n ) , W) . (4.3)
n =1
Para simplificarmos os cálculos, substituindo produtos por somas, introduzimos, como
anteriormente, uma função erro (ou energia) :
E ( W) = − ln L( W)
P (4.4)
= −∑ ln p(t ( n ) x ( n ) , W)
n =1

Com um modelo de ruído gaussiano teremos:
1  (t − y ( x; W )) 2 
p (t x, W) = p (t − y ( x; W )) = exp  −  (4.5)
2πσ  2σ 2 

Substituindo (4.5) em (4.4) e ignorando os termos que não dependem dos parâmetros
W teremos:
1 P
E ( W) = ∑  y ( x( n ) ; W) − t ( n )  .
2
  (4.6)
2 n =1
Uma outra possibilidade é assumirmos um ruído com densidade exponencial
generalizada:
1
rβ
( )
r
p (t x, W ) =exp − β t − y ( x; W ) ,
r
(4.7)
2Γ(1/ r )
neste cado teremos a seguinte função erro para minimizar dado o conjunto de dados D.

1 P
∑  y ( x( n ) ; W) − t ( n ) 
r
E ( W) = (4.8)
2 n =1  
Qualquer que seja o método de otimização que empregemos (Gradiente Conjugado
Escalado, Quase-Newton, etc) é necessário cacular o gradiente da função erro. No caso
de uma MLP, há uma maneira bastante eficiente de realizar este cálculo proposta
inicialmente na década de sessenta e depois redescoberta várias vezes, esta técnica é
conhecida como algoritmo Backpropagation2.

2
Amari S., Theory of adaptive pattern classifiers, IEEE Trans EC-16 299 (1967).

63

Backpropagation

No caso mais simples, devemos calcular o gradiente da seguinte função erro:
2
1 P M  N  
E ( W) = ∑  ∑ wm 0ϕ m  ∑ w jm x (jn ) + w0  + w0 − t ( n ) 
out
(4.9)
2 n=1  m=1
  j =1  


Para simplificarmos os cálculos, assumiremos, sem perda de generalidade que os limiares
w0 são pesos sinápticos que recebem sinais constantes x=1. Também assumiremos que as
funções de transferência da camada escondida são " ( z ) " tanh( z ) Assim:
2
1 P M  N  
E ( W) = ∑  ∑ wm 0 tanh  ∑ w jm x (jn )  − t ( n )  . (4.10)
2 n =1  m =1
  j =1  

Aqui introduzimos a notação w jm para indicar conexões sinápticas unindo a entrada j
ao neurônio m da camada escondida . Agora definimos o campo pós-sináptico atuando
sobre o neurônio m quando o sinal de entrada é x( n ) :
N
hmn ) " ) w jm x (jn ) (4.11)
(

j "1

A função erro pode ser decomposta em contribuições de cada componente do conjunto
D:
P
E ( W) = ∑ E ( n ) ( W) (4.12)
n =1
Com
2
1 M 
E ( W) =  ∑ wm 0 amn ) − t ( n )  ,
(n) (
(4.13)
2  m =1 
onde aproveitamos a interpretação do modelo descrito por (4.1) como uma rede de
neurônios para introduzimos amn ) " tanh(hmn ) ) como a saída do neurônio m da camada
( (

escondida quando o sinal de entrada é x ( n ) . Por consistência o campo pós-sináptico na
M
camada externa é h0( n ) " ) wm 0 amn ) e a saída y ( n ) " h0n ) . Graficamente teremos:
( (

m"1

h0( n ) y (n)

amn )
(

hmn )
(

x(n)

64

O gradiente em relação aos pesos sinápticos será:
*E P
*E ( n ) *hmn )
(
" ) (n) (4.14)
*w jm n"1 *hm *w jm

*E ( n )
Definimos o erro #mn ) "
(
e assim teremos que :
*hmn )
(

*E P
" ) #mn ) xmn )
( (
(4.15)
*w jm n"1

Para o neurônio de saída o cálculo de #0n ) é trivial resultando em:
(

∂E ( n )
δ 0( n ) = = h0( n ) − t ( n ) (4.16)
∂h0( n )
d tanh( z )
Lembrando que " 1# tanh 2 ( z ) , para os neurônios da camada interna teremos:
dz
*E ( n ) + M , (n)
.) w a ( n ) # t ( n ) - w dam
#m " ( n ) " .
(n)
- m0 (n)
-
*hm . m"1 m 0 m
/ 0 dhm , (4.17)
" #0n ) wm 0 (1# amn ) amn ) )
( ( (

conhecida como fórmula de retropropagação (backpropagation).

Note que para o cálculo de derivadas na camada interna é necessário utilizar erros da
camada mais externa. Pictorialmente o algoritmo consiste na seguinte seqüência:

1. Dada a entrada x ( n ) , calculam-se os campos pós-sinápticos hmn ) por toda a rede.
(

h0( n )

hmn )
(

x(n)

N M
Assim hmn ) " ) w jm x (jn ) e h0( n ) " ) wm 0 tanh(hmn ) ) .
( (

j "1 m"1

65

2. Calcula-se o erro na saída #0n ) e retropropaga-se para as camadas interiores
(

utilizando #mn ) " #0( n ) wm 0 (1# tanh 2 (hmn ) )) .
( (

# 0( n )

#mn )
(

*E P
*E P
3. Calcula-se os gradiente utilizando " ) #mn ) x (jn ) e
(
" ) #0( n ) amn ) .
(

*w jm n"1 *wm 0 n"1

amn )
(

x (j n )

O Backpropagation reduz o número de operações necessárias para o cálculo de gradientes
em MLPs de O(W 2 ) para O(W ) , onde W é o número de parâmetros. Calculado o
gradiente podemos utilizar qualquer um dos algoritmos de otimização conhecidos para
efetuar o treinamento da rede.

Perceptron Multicamada: Classificação

Uma classificação simples é uma função f : ! M ! {#1,1} . Uma rede neural pode ser
treinada a reconhecer uma função de classificação a partir de um conjunto de treinamento
D " {x( n ) , t ( n ) }n"1 . Um perceptron de camada única definido como
P

N
y (x; w ) " "() w j x j & w0 ) , (4.18)
j "1

66

onde " é uma função sigmoidal (tanh, erf, ...) divide o espaço em duas regiões separadas
por um hiperplano definido por w 1 x " #w0 . Assim qualquer vetor com w 1 x 2 #w0 é
classificado como +1 e qualquer vetor com w 1 x 3 #w0 é classificado como -1. Ilustrando:

+

-

A distância do hiperplano até a origem é w0 . Uma MLP com uma camada escondida
pode representar qualquer região convexa no espaço. Cada neurônio da camada
escondida define um hiperplano e a classificação é definida pela unidade de saída.

M  N  
y (x, W ) = ϕ 0  ∑ wm 0ϕ  ∑ w jm x j + w0  + w0 
out
(4.19)
 m =1
  j =1  

1
Normalmente se utiliza " ( z ) " tanh( z ) para a camada interna e "0 ( z ) " para a
1 & e# z
camada externa. A região convexa definida é mais complicada que um simples polígono
devido ao uso de funções diferenciáveis. Para obtermos regiões arbitrárias é necessário
utilizar uma rede com duas camadas escondidas:

L
 M  N   3

y (x, W) = ϕ 3 ∑ wl 0ϕ 2  ∑ wmlϕ1  ∑ w jm x j + w1  + w0  + w0  .
0
2

 l =1
  m =1
  j =1  
 

Este tipo de rede é um classificador universal do mesmo modo que uma MLP com uma
camada escondida pode representar qualquer função contínua3.

3
Lipmann, R. P. (1987). Na introduction to computing with neural nets. IEEE ASSP Magazine, April, 4-22.

67

MLPs em Netlab

O Netlab trás um conjunto de funções para a implementação de MLPs com uma camada
escondida. As principais funções disponíveis são:

mlp: cria uma MLP com uma camada escondida;
mlpinit: inicia os pesos com variância definida;
mlpgrad: calcula o gradiente do erro;
mlpfwd: calcula a sída da rede;

Outras funções podem ser obtidas entrando
> help netlab;

Demonstraremos agora o uso do Netlab para uma tarefa de regressão. O problema
consiste na interpretação automática do resultado de doze sensores utilizados em
oleodutos para a determinação da proporção de gás, óleo e água em um fluxo. Primeiro
500 medidas são efetuadas em laboratório, 400 destas medidas são então utilizadas para
treinar uma MLP as outras 100 são utilizadas para teste. Os dados estão armazenados no
arquivo "oleoduto.dat", as doze primeiras colunas deste arquivo são as medidas dos
sensores as últimas duas colunas são a proporção de água e gás respectivamente.

Começamos por carregar o conjunto de dados em uma matriz "oleoduto":
> load 'oleoduto.dat'

A seguir separamos os dados em quatro vetores: inteste, intreino, outteste, outtreino.

>intreino=oleoduto(1:400,1:12);
>inteste = oleoduto(401:500,1:12);
>outtreino = oleoduto (1:400,13:14);
> outteste = oleoduto (401:500, 13:14);

De posse de nossos vetores de treinamento e teste, podemos agora criar uma MLP:
> net = mlp(12,7,2,'linear');

68

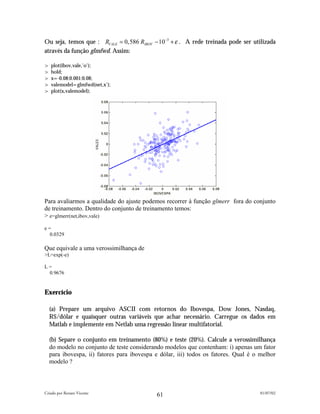
A arquitetura que escolhemos tem a seguinte representação:

As unidades de saída são lineares e as unidades internas são tanh .

Podemos ver a rede criada digitando:
>net

net =
type: 'mlp'
nin: 12
nhidden: 7
nout: 2
nwts: 107
actfn: 'linear'
w1: [12x7 double]
b1: [-0.1817 0.3313 -0.2486 0.0904 -0.1714 -0.3418 0.3177]
w2: [7x2 double]
b2: [0.1880 0.5289]

Note que o modelo contém 107 parâmetros. Agora inicializamos o vetor de controle
dos algoritmos de otimização:

>options=foptions;

Ajustamos o vetor de controles para que os erros sejam exibidos na tela:
>options(1)=1;
Ajustamos o número máximo de iterações para 500;
>options(14)=500;

69

Agora treinamos a MLP utilizando o Gradiente Conjugado Escalado (scg):
> [net,options,erro] = netopt(net,options,intreino,outtreino,'scg');

…
Cycle 200 Error 0.160426 Scale 1.000000e-015

Agora plotamos a evolução do erro de treinamento com o número de iterações:

> plot(err,'o-');

Agora utilizamos o modelo treinado armazenado em net para realizar prediçõe no
conjunto de teste:
> outmodel=mlpfwd(net,inteste);

70

A seguir plotamos as previsões contra os valores reais no conjunto de teste:
> plot(outmodel(:,1),outteste(:,1),'o');

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

> plot(outmodel(:,2),outteste(:,2),'o');

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8

Se a qualidade das predições é adequada ou não irá depender da aplicação. Podemos
quantificar esta qualidade calculando a diferença percentual média entre previsões e
valores experimentais definida como:
1 P outmodel # outteste
(n) (n)

4" ) (4.20)
P n"1 outteste(n)
>deltas=abs(outmodel-outteste)./outteste;
> delta=sum(deltas)./100

delta =
0.2654 0.1465

Ou seja o erro médio é de 26,5% para a primeira saída (óleo) e 14,65% para a segunda
saída (água). Adcionalmente é interessante observarmos o perfil geral das previsões:

71

> plot(deltas(:,1),'o-'); figure; plot(outteste(:,1),'o-');
> plot(deltas(:,2),'o-'); figure; plot(outteste(:,2),'o-');
18

16

14

12

10

8

6

4

2

0
0 10 20 30 40 50 60 70 80 90 100

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0
0 10 20 30 40 50 60 70 80 90 100

4

3.5

3

2.5

2

1.5

1

0.5

0
0 10 20 30 40 50 60 70 80 90 100

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0
0 10 20 30 40 50 60 70 80 90 100

72

Nota-se que grandes erros estão relacionados com valores pequenos das saídas. Uma
forma de melhorar a qualidade das previsões é utilizar apenas valores de saída acima de
um certo limiar, para isso é necessário modificar a arquitetura da rede adicionando uma
terceira saída definida como outtreino(:,3)=1 - outtreino(:,1) – outtreino (:,2) , treinar
novamente o modelo e apenas utilizar as duas previsões que exibirem valores acima de
um limiar definido (por exemplo: >0,1). A terceira previsão pode ser obtida da
condição de normalização.

Aplicações de MLPs

O sucesso de uma aplicação de MLPs depende da natureza do problema. Se há uma
função, mesmo que complexa, subjacente aos dados, as chances de sucesso são grandes.

Há uma grande quantidade de aplicações de MLPs e outras redes descritas na Internet,
para citar alguns links:

http://www.brainstorm.co.uk/NCTT/Welcome.htm
http://www.emsl.pnl.gov:2080/proj/neuron/neural/products/
http://neuralnetworks.ai-depot.com/Applications.html

Exercício

1. Melhore a qualidade das previsões do modelo para composição de fluxos em
oleodutos realizando as seguintes modificações :
a) Gere conjuntos de treinamento e teste com três saídas que somem um;
b) Treine uma rede com 7 neurônios na camada escondida do mesmo modo
apresentado ;
c) Na etapa de teste, utilize o seguinte algoritmo para efetuar previsões:
tome as duas saídas com maior valor out1 e out2, obtenha a terceira saída
com out3=1-out1-out2;
d) Calcule o erro percentual médio para cada uma das saídas assim obtidas.
e) Repita o treinamento para redes com 5,6,8,10 e 15 neurônios. Qual é a
melhor arquitetura ?

73

62

Redes neurais com matlab

Mais conteúdo relacionado

Mais procurados

Destaque

Semelhante a Redes neurais com matlab

Mais de Renato Vicente

Último

Redes neurais com matlab