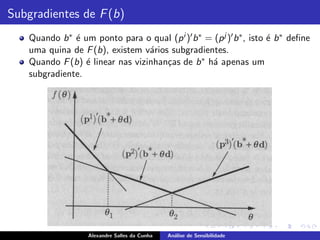
O documento apresenta uma introdução à análise de sensibilidade em problemas de programação linear, descrevendo como pequenas alterações nos parâmetros do problema, como adição de variáveis, restrições ou modificações nos vetores b, c, podem afetar as soluções ótimas. A análise de sensibilidade permite avaliar o impacto dessas alterações sem precisar resolver o problema do zero.

1. An´lise de Sensibilidade
a
Alexandre Salles da Cunha
DCC-UFMG, Abril 2010
Alexandre Salles da Cunha An´lise de Sensibilidade
a

2. Par primal-dual
min c ′x
max p ′b
Ax = b
p′A ≤ c ′
x ≥0
An´lise de sensibilidade envolver´ avaliar o impacto nas solu¸˜es ´timas
a a co o
x ∗ , p ∗ do par primal-dual quando houver:
Adi¸˜o, remo¸˜o de uma nova vari´vel.
ca ca a
Adi¸˜o de uma restri¸˜o de desigualdade e igualdade.
ca ca
Modifica¸˜es nos vetores b, c.
co
Modifica¸˜es em colunas b´sicas e n˜o b´sicas Aj .
co a a a
A id´ia da an´lise de sensibilidade consiste em tentar restaurar a
e a
otimalidade diante das perturba¸˜es acima, sem resolver o PL ”do zero”.
co
Alexandre Salles da Cunha An´lise de Sensibilidade
a

3. Adi¸˜o de uma nova vari´vel
ca a
Vamos supor que uma nova vari´vel xn+1 com custo cn+1 e coluna
a
tecnol´gica An+1 seja inserida no PL.
o
Claramente dispor de uma nova vari´vel n˜o altera a viabilidade da
a a
solu¸˜o b´sica corrente. Em particular, (x ∗ , 0) ´ uma solu¸˜o b´sica
ca a e ca a
vi´vel para o novo programa linear.
a
Assim sendo, a solu¸˜o x ∗ continuar´ b´sica ´tima se a restri¸˜o dual
ca a a o ca
associada ` nova vari´vel for satisfeita pela base B associada a x ∗ .
a a
Condi¸˜o a verificar
ca
Diante da introdu¸˜o de xn+1 x ∗ permanece ´tima se
ca o
c n+1 = cn+1 − cB B −1 An+1 ≥ 0.
Caso c n+1 < 0, continuamos o m´todo Simplex tendo como base
e
inicial avan¸ada a base ´tima do programa anterior.
c o
Alexandre Salles da Cunha An´lise de Sensibilidade
a

4. Adi¸˜o de nova vari´vel - exemplo
ca a
Problema Original cuja solu¸˜o ´tima ´ (2, 2, 0, 0) e o
ca o e
quadro ´timo ´:
o e
min −5x1 − x2 + 12x3 x1 x2 x3 x4
3x1 + 2x2 + x3 = 10 w= 12 0 0 2 7
5x1 + 3x2 + x4 = 16 x1 = 2 1 0 -3 2
x2 = 2 0 1 5 -3
x1 . . . x4 ≥ 0
Introduzindo a vari´vel x5 com custo c5 = −1 e A5 = (1 1)′ , e notando
a
−1 ´ dada pelas duas ultimas colunas no Tableau
que neste caso B e ´
anterior, temos o novo quadro:
x1 x2 x3 x4 x5
w= 12 0 0 2 7 -4
x1 = 2 1 0 -3 2 -1
x2 = 2 0 1 5 -3 2
Alexandre Salles da Cunha An´lise de Sensibilidade
a

5. Adi¸˜o de nova vari´vel - exemplo
ca a
Fazendo o pivoteamento correspondente a entrada de x5 e sa´ de x2 ,
ıda
temos:
Quadro original
x1 x2 x3 x4 x5
w= 12 0 0 2 7 -4
x1 = 2 1 0 -3 2 -1
x2 = 2 0 1 5 -3 2
Quadro ´timo resultante
o
x1 x2 x3 x4 x5
w= 16 0 2 12 1 0
x1 = 3 1 0.5 -0.5 0.5 0
x5 = 1 0 0.5 2.5 -1.5 1
Alexandre Salles da Cunha An´lise de Sensibilidade
a

6. Adi¸˜o de uma restri¸˜o - desigualdade
ca ca
′
Vamos assumir que am+1 x ≥ bm+1 seja inserida no PL.
Introduzimos uma vari´vel de folga xn+1 , reescrevemos a restri¸˜o
a ca
′
am+1 x − xn+1 = bm+1 para obter um problema novamente na forma
padr˜o, definido pelo poliedro P = {x ∈ Rn+1 : Ax = b} onde:
a +
A 0 b
A= ′ ,b =
am+1 −1 bm+1
Se B denota a base ´tima do programa anterior, a base associada ao
o
B 0
novo programa, B ´ dada por B =
e , onde a′ ´ o vetor de
e
a′ −1
m entradas de am+1 correspondente aos ´ ındices das colunas b´sicas
a
−1 B −1 0
que definem B. N˜o ´ dif´ verificar que B =
a e ıcil
a′ B −1 −1
O novo vetor de custos reduzidos ´ dado por
e
′ 0 − c′ B −1 0 A 0
c= c B 0 =
a′ B −1 −1 ′
am+1 −1
−1
(c ′ − cB B −1 A) 0
′ ≥ 0, logo B ´ dual vi´vel.
e a
Alexandre Salles da Cunha An´lise de Sensibilidade
a

7. Introdu¸˜o de uma desigualdade - exemplo
ca
Introduzindo a restri¸˜o x1 + x2 ≥ 5 no PL do exemplo anterior:
ca
Problema Original
Quadro ´timo:
o
min −5x1 − x2 + 12x3 x1 x2 x3 x4
w= 12 0 0 2 7
3x1 + 2x2 + x3 = 10
x1 = 2 1 0 -3 2
5x1 + 3x2 + x4 = 16 x2 = 2 0 1 5 -3
x1 . . . x4 ≥ 0
Quadro dual vi´vel, de partida para o Dual Simplex
a
x1 x2 x3 x4 x5
w= 12 0 0 2 7 0
x1 = 2 1 0 -3 2 0
x2 = 2 0 1 5 -3 0
x5 = -1 0 0 2 -1 1
Alexandre Salles da Cunha An´lise de Sensibilidade
a

8. Introdu¸˜o de uma desigualdade - exemplo
ca
Quadro dual vi´vel, de partida para o Dual Simplex
a
x1 x2 x3 x4 x5
w= 12 0 0 2 7 0
x1 = 2 1 0 -3 2 0
x2 = 2 0 1 5 -3 0
x5 = -1 0 0 2 -1 1
Sai da base: x5 , entra na base: x4
Quadro final resultante
x1 x2 x3 x4 x5
w= 5 0 0 16 0 0
x1 = 0 1 0 1 0 0
x2 = 8 0 1 -15 0 0
x4 = 1 0 0 -2 1 -1
Alexandre Salles da Cunha An´lise de Sensibilidade
a

9. Introdu¸˜o de restri¸˜o de igualdade
ca ca
ca ′
Adicionamos a restri¸˜o am+1 x = bm+1 , violada pela solu¸˜o ´tima do PL
ca o
anterior.
Novo dual
max p ′ b + pm+1 bm+1
p ′ A + pm+1 am+1 ≤ c ′
Se p ∗ denota a solu¸˜o b´sica ´tima do dual anterior, (p ∗ , 0) ´ uma
ca a o e
solu¸˜o vi´vel para o novo dual.
ca a
Sendo p ∗ b´sica, temos que m das restri¸˜es duais p ′ A ≤ c ′ s˜o
a co a
linearmente independentes e ativas.
Entretanto, para o novo ponto dual (p ∗ , 0), n˜o temos a garantia de
a
′A + p ′
que m + 1 restri¸˜es duais li dentre p
co m+1 am+1 ≤ c ser˜o a
justas. Assim sendo, n˜o podemos garantir que (p
a ∗ , 0) ´ uma solu¸˜o
e ca
b´sica para o novo poliedro dual.
a
Alexandre Salles da Cunha An´lise de Sensibilidade
a

10. Introdu¸˜o de restri¸˜o de igualdade
ca ca
Assumimos que am+1 x ∗ > bm+1 e M suficientemente grande e
′
introduzimos o PL auxiliar:
min c ′ + Mxn+1
Ax = b
′
am+1 x − xn+1 = bm+1
x ≥ 0, xn+1 ≥ 0
Uma base inicial vi´vel para o PL acima ´ obtida usando-se as
a e
colunas b´sicas que definiem x ∗ e a coluna associada a xn+1 . A
a
B 0
matriz b´sica resultante B =
a ´ vi´vel para o PL auxiliar.
e a
a′ −1
Por este motivo, reotimizamos com o Simplex Primal aplicado
partindo da base vi´vel B.
a
Se na solu¸˜o do PL otimizado, M for suficientemente grande e o
ca
programa for vi´vel, teremos xn+1 = 0.
a
Alexandre Salles da Cunha An´lise de Sensibilidade
a

11. Modifica¸˜es no vetor de fatores b
co
Desejamos avaliar as modifica¸˜es implicadas por alterar b para b + δei :
co
Se B −1 (b + δei ) ≥ 0, a otimalidade da solu¸˜o b´sica anterior ´
ca a e
garantida (nada mudou no dual).
Avaliando condi¸˜es para B −1 (b + δei ) ≥ 0
co
Seja g = (β1i , β2i , . . . , βmi ) a i -´sima coluna de B −1 .
e
Ent˜o B −1 (b + δei ) ≥ 0 implica que:
a
xB + δg ≥ 0 ou
xB(j) + δβji ≥ 0 j = 1, . . . , m.
Equivalentemente:
xB(j )
◮ δ≥− βji , se βji > 0
xB(j
◮ δ≤ − βji ) , se βji < 0
Alexandre Salles da Cunha An´lise de Sensibilidade
a

12. Modifica¸˜es no vetor de fatores b - exemplo
co
´
Vamos considerar modificar b1 para b1 + δ no Tableau Otimo dado por:
x1 x2 x3 x4
w= 12 0 0 2 7
x1 = 2 1 0 -3 2
x2 = 2 0 1 5 -3
Observe que g = (−3 5) e ent˜o temos:
a
x1 = 2 − 3δ ≥ 0 → δ ≤ 2 .
3
x2 = 2 + 5δ ≥ 0 → δ ≥ − 2
5
Alexandre Salles da Cunha An´lise de Sensibilidade
a

13. Modifica¸˜es no vetor de custos c
co
Vamos considerar as implica¸˜es decorrentes de modificar cj para cj + δ, o
co
custo de uma vari´vel n˜o b´sica j:
a a a
A modifica¸˜o n˜o afeta a viabilidade primal, apenas a viabilidade
ca a
dual (otimalidade dual).
Se cj + δ − cB B −1 Aj ≥ 0 ou seja se δ ≥ −c j a base anterior continua
o
´tima. Caso esta condi¸˜o n˜o se verifique, aplicamos o primal
ca a
simplex, introduzindo a vari´vel xj na base.
a
Alexandre Salles da Cunha An´lise de Sensibilidade
a

14. Modifica¸˜es no custo de uma vari´vel b´sica
co a a
Vamos considerar as implica¸˜es decorrentes de modificar cj para
co
cj + δ, o custo de uma vari´vel b´sica j.
a a
Vamos assumir que j seja a vari´vel b´sica associada ` l −´sima linha
a a a e
do Tableau, isto ´ j = B(l ) e ent˜o cB = cB + δel .
e a
Temos que assegurar que (cB + δel )B −1 Ai ≤ ci , ∀i = j, uma vez que
todos os custos reduzidos, exceto c j s˜o afetados pela modifica¸˜o.
a ca
Definindo qli como a l -´sima entrada do vetor B −1 Ai temos que
e
δqli ≤ c i , ∀i = j.
Alexandre Salles da Cunha An´lise de Sensibilidade
a

15. Exemplo - modifica¸˜es nos custos
co
Para o exemplo anterior:
x1 x2 x3 x4
w= 12 0 0 2 7
x1 = 2 1 0 -3 2
x2 = 2 0 1 5 -3
Modifica¸˜es admiss´
co ıveis (que ainda preservam a otimalidade da base
atual) nas vari´veis:
a
N˜o b´sicas:
a a
◮ δ3 ≥ −c 3 = −2
◮ δ4 ≥ −c 4 = −7
B´sicas: adicionando δ1 a c1 , temos para j = 1, B(1) = 1,
a
q12 = 0, q13 = −3, q14 = 2.
◮ δ1 q12 ≤ c2 , triv. satisfeita.
2
◮ δ1 q13 ≤ c3 → δ1 ≥ − 3
7
◮ δ1 q14 ≤ c4 → δ1 ≥ 2
Alexandre Salles da Cunha An´lise de Sensibilidade
a

16. Mudan¸as no vetor tecnol´gico Aj
c o
Caso 1: j ´ uma vari´vel n˜o b´sica:
e a a a
A viabilidade da base ´tima (em rela¸˜o ao primal) n˜o ´ afetada.
o ca a e
´
E necess´rio verificar se a otimalidade (viab. dual) ´ afetada, atrav´s
a e e
da n˜o negatividade do custo reduzido c j .
a
Vamos considerar que a entrada aij de A foi alterada para aij + δ.
Ent˜o precisamos garantir que cj − p ′ (Aj + δei ) ≥ 0 ou
a
equivalentemente c j − δpi ≥ 0, onde p ′ = cB B −1 .
′
Caso a condi¸˜o acima seja violada, j deve entrar na base (Primal
ca
Simplex).
Alexandre Salles da Cunha An´lise de Sensibilidade
a

17. Mudan¸as no vetor tecnol´gico Aj
c o
Caso 2: j ´ uma vari´vel b´sica:
e a a
A viabilidade da base ´tima pode ser afetada, tanto no primal quanto
o
no dual.
Assumindo que aij seja alterado para aij + δ, o conjunto de valores
admiss´ıveis para a varia¸˜o resultar ainda em uma base ´tima ´ um
ca o e
intervalo (assim como nos casos anteriores).
Assumindo solu¸˜o primal e dual ´timas n˜o dengeradas dadas por
ca o a
x ∗ , p, se a coluna Aj for modificada para Aj + δei temos que:
c ′ x(δ) = c ′ x ∗ − δxj∗ pi + O(δ2 )
Interpreta¸˜o em termos do problema da dieta: se aij aumenta em δ,
ca
ganhamos de gra¸a, δ unidades do nutriente i por unidade do
c
alimento j. Uma vez que pi denota o custo marginal do nutriente i ,
δpi xj∗ denota a redu¸˜o de custo esperada.
ca
Alexandre Salles da Cunha An´lise de Sensibilidade
a

18. Dependˆncia da otimalidade em fun¸˜o de b
e ca
Reescrevendo a regi˜o de viabilidade primal para deixar expl´
a ıcita a
dependˆncia do vetor b, temos que
e
P(b) = {x : Ax = b, x ≥ 0}
Vamos definir S = {b : P(b) = ∅}.
Observe ent˜o que S pode ser reescrito como S = {Ax : x ≥ 0} que ´
a e
um conjunto convexo.
Para qualquer vetor b ∈ S, vamos redefinir o custo ´timo do
o
Problema primal como:
F (b) = minx∈P(b) c ′ x
Alexandre Salles da Cunha An´lise de Sensibilidade
a

19. Dependˆncia da otimalidade em fun¸˜o de b
e ca
Vamos assumir que o espa¸o dual p ′ A ≤ c ′ seja n˜o vazio.
c a
Por dualidade, temos que F (b) > ∞, ∀b ∈ S, isto ´, o problema
e
primal admite ´timo finito para todo b.
o
Vamos tentar compreender a estrutura da fun¸˜o F (b), b ∈ S. Para
ca
tanto, vamos nos fixar em um determinado b ∗ ∈ S.
Vamos supor que o objetivo ´timo F (b ∗ ) ´ dada por uma base ´tima
o e o
B associada a uma solu¸˜o b´sica xB = B −1 b ∗ n˜o degenerada e que
ca a a
o correspondente vetor de custos reduzidos seja n˜o negativo.
a
Alexandre Salles da Cunha An´lise de Sensibilidade
a

20. Dependˆncia da otimalidade em fun¸˜o de b
e ca
Sendo n˜o denenerada, podemos modificar b ∗ para b e desde que
a
b ∗ − b seja suficientemente pequena B −1 b ≥ 0 ser´ uma solu¸˜o
a ca
b´sica vi´vel ´tima para o problema perturbado.
a a o
Logo, para b suficientemente pr´ximo de b ∗ , F (b) = cB B −1 b = p ′ b.
o ′
Isto ´, nas vizinhan¸as de b ∗ , F (b) ´ uma fun¸˜o linear de b e seu
e c e ca
gradiente ´ dado por p.
e
Teorema
O custo ´timo F (b) ´ uma fun¸˜o convexa de b no conjunto S.
o e ca
Alexandre Salles da Cunha An´lise de Sensibilidade
a

21. Estrutura de F (b)
Teorema
O custo ´timo F (b) ´ uma fun¸˜o convexa de b no conjunto S.
o e ca
Prova
Tomemos b 1 , b 2 ∈ S e seja x i : i = 1, 2 as correspondentes solu¸˜es
co
que minimizam F (b 1 ), F (b 2 ), respectivamente.
Tome um escalar λ ∈ [0, 1] e defina y = λx 1 + (1 − λ)x 2 :
◮ y ∈ P(λb 1 + (1 − λ)b 2 ) → y ´ vi´vel.
e a
Observe que:
F (λb 1 + (1 − λ)b 2 ) ≤ c ′y
= λc ′ x 1 + (1 − λ)c ′ x 2
= λF (b 1 ) + (1 − λ)F (b 2 )
Alexandre Salles da Cunha An´lise de Sensibilidade
a

22. Elaborando melhor o Teorema anterior
Vamos elaborar o Teorema, avaliando agora o dual abaixo, que assumimos
ser vi´vel:
a
max p′b
p′A ≤ c ′
Por dualidade, para todo b ∈ S, F (b) = ′b para algum p.
Sendo A uma matriz de posto m (completo), o poliedro dual possui
pelo menos um ponto extremo.
Sejam p 1 , . . . , p N os pontos extremos do poliedro dual.
Ent˜o temos que F (b) = maxi =1,...,N (p i )′ b, b ∈ S
a
Alexandre Salles da Cunha An´lise de Sensibilidade
a

23. Interpretando F (b) = maxi=1,...,N (p i )′b, b ∈ S
F ´ dado pelo m´ximo de uma cole¸˜o finita de fun¸˜es lineares.
e a ca co
F ´ ent˜o dado pelo envelope superior de um conjunto finito de
e a
fun¸˜es lineares, sendo ent˜o linear por partes e convexa (prova
co a
alternativa do teorema anterior).
Alexandre Salles da Cunha An´lise de Sensibilidade
a

24. Sobre a diferenciabilidade de F (b) em rela¸˜o a b
ca
Para alguns valores de b (nos pontos onde duas fun¸˜es lineares
co
(p i )′ b e (p j )′ b se encontram), F (b) n˜o ´ diferenci´vel.
a e a
Nestes pontos, o programa dual admite mais de uma solu¸˜o otima.
ca ´
Para tais valores de b, qualquer combina¸˜o linear convexa de p i e p j
ca
fornecem um vetor dual ´timo (subgradiente de F (b) em b !).
o
Consequentemente, para estes valores de b a solu¸˜o primal ´
ca e
degenerada. Vimos que para uma solu¸˜o primal n˜o degenerada,
ca a
F (b) ´ localmente linear com b, n˜o podendo ser associada a um
e a
ponto n˜o diferenci´vel de F (b).
a a
Alexandre Salles da Cunha An´lise de Sensibilidade
a

25. Comportamento de F (b)
Vamos avaliar o comportamento de F (b) quando um determinado
tipo de modifica c˜o ocorre em b ∗ .
a
Vamos verificar o que ocorre com F (b) quando, para b ∗ e d fixos,
b = b ∗ + θd, para θ um escalar.
Pela defini¸˜o de F (b) temos que:
ca
F (b(θ)) = F (θ) = maxi =1,...,N (p i )′ (b ∗ + θd), b ∗ + θd ∈ S
Alexandre Salles da Cunha An´lise de Sensibilidade
a

26. O conjunto de solu¸˜es duais ´timas
co o
Defini¸˜o - subgradiente
ca
Seja F uma fun¸˜o convexa definida em um conjunto convexo S. Seja b ∗
ca
um elemento de S. Dizemos que um vetor p ´ um subgradiente de F em
e
b ∗ se:
F (b ∗ ) + p ′ (b − b ∗ ) ≤ F (b), ∀b ∈ S
Para a defini¸˜o do subgradiente, n˜o ´ feita nenhuma hip´tese de
ca a e o
diferenciabilidade de F .
Observe que o subgradiente generaliza o conceito de gradiente para
uma fun¸˜o convexa diferenci´vel definida em um conjunto convexo.
ca a
Alexandre Salles da Cunha An´lise de Sensibilidade
a

27. Subgradientes de F (b)
Quando b ∗ ´ um ponto para o qual (p i )′ b ∗ = (p j )′ b ∗ , isto ´ b ∗ define
e e
uma quina de F (b), existem v´rios subgradientes.
a
Quando F (b) ´ linear nas vizinhan¸as de b ∗ h´ apenas um
e c a
subgradiente.
Alexandre Salles da Cunha An´lise de Sensibilidade
a

28. O conjunto de solu¸˜es duais ´timas
co o
Teorema
Assuma que o problema min c ′ x, x ∈ P(b ∗ ) assuma custo ´timo finito.
o
Ent˜o o vetor p ´ uma solu¸˜o ´tima para o problema dual associado se e
a e ca o
somente se p for um subgradiente de F (b) em b ∗ .
Prova: →
Por dualidade forte temos p ′ b ∗ = F (b ∗ ).
Tome b ∈ S e x ∈ P(b). Por dualidade fraca temos p ′ b ≤ c ′ x.
ınimo em x temos que p ′ b ≤ F (b).
Tomando o m´
Ent˜o p ′ b − p ′ b ∗ ≤ F (b) − F (b ∗ ) que implica que
a
F (b ∗ ) + p ′ (b − b ∗ ) ≤ F (b) e logo p ´ um subgradiente de F em b ∗ .
e
Alexandre Salles da Cunha An´lise de Sensibilidade
a

29. O conjunto de solu¸˜es duais ´timas
co o
Prova: ←
Hip´tese: F (b ∗ ) + p ′ (b − b ∗ ) ≤ F (b) (p ´ subgradiente).
o e
Tome x ≥ 0, seja b = Ax e observe que x ∈ P(b).
Por dualidade fraca F (b) ≤ c ′ x.
Ent˜o temos:
a
p ′ Ax = p ′b
≤ F (b) − F (b ∗ ) + p ′ b ∗
≤ c ′ x − F (b ∗ ) + p ′ b ∗
Uma vez que p ′ Ax ≤ c ′ x − F (b ∗ ) + p ′ b ∗ deve valer para qualquer x e
que −F (b ∗ )p ′ b ∗ ´ um valor que independe de x, p ′ A ≤ c ′ . Logo p ′ ´
e e
dual vi´vel.
a
Em particular para x = 0 temos F (b ∗ ) ≤ p ′ b ∗ . Por dualidade fraca
temos que toda solu¸˜o dual vi´vel q satisfaz q ′ b ≤ F (b ∗ ) ≤ p ′ b ∗ .
ca a
∗ ´ ´tima para o dual.
Logo p e o
Alexandre Salles da Cunha An´lise de Sensibilidade
a

30. Avalia¸˜o da otimalidade em fun¸˜o de c
ca ca
Vamos desenvolver racioc´ an´logo para a dependˆncia da
ınio a e
otimalidade em fun¸˜o de modifica¸˜es no vetor de custos c.
ca co
Manteremos A e b fixos e perturbaremos c.
Para tanto, vamos considerar o espa¸o de viabiliade dual p ′ A ≤ c ′ .
c
Vamos definir Q(c) = {p : p ′ A ≤ c ′ } e T = {c : Q(c) = ∅}.
Dados c 1 , c 2 ∈ T , existem p 1 , p 2 (respectivamente) tais que
(p i )′ A ≤ c ′ . Para qualquer escalar λ ∈ [0, 1], temos
(λ(p 1 )′ + (1 − λ)(p 2 )′ )A ≤ λ(c 1 )′ + (1 − λ)(c 2 )′ e portanto
λ(p 1 )′ + (1 − λ)(p 2 )′ ∈ T .
Consequentemente T ´ convexo.
e
Alexandre Salles da Cunha An´lise de Sensibilidade
a

31. Avalia¸˜o da otimalidade em fun¸˜o de c
ca ca
Tomando c ∈ T (dual invi´vel), o problema primal ´ ilimitado. Por
a e
outro lado, se c ∈ T o custo primal ´ finito.
e
Ent˜o vamos assumir que c ∈ T e vamos denotar o custo primal
a
o
´timo por G (c).
Vamos denotar por x 1 , . . . , x N as solu¸˜es b´sicas do poliedro
co a
n : Ax = b}. Assim sendo, temos que
{x ∈ R+
G (c) = mini =1,...,N c ′ x i
e G (c) corresponde ao envelope inferior de uma cole¸˜o de fun¸˜es ´
ca co e
lineares, sendo uma fun¸˜o linear por partes concava.
ca
Alexandre Salles da Cunha An´lise de Sensibilidade
a

32. Avalia¸˜o da otimalidade em fun¸˜o de c
ca ca
Se para um valor c ∗ o programa primal admite uma unica solu¸˜o
´ ca
´tima x i , ent˜o temos que (c ∗ )′ x i < (c ∗ )′ x j : ∀j = i .
o a
Para todo c suficientemente pr´ximo a c ∗ , (c ∗ )′ x i < (c ∗ )′ x j : ∀j = i
o
deve continuar valendo. Desta forma, para solu¸˜es primais unicas
co ´
G (c) = c ∗ x i .
Para o caso de solu¸˜o primal m´ltipla, o correspondente valor de c
ca u
deve ser induzir uma quina de G (c).
Alexandre Salles da Cunha An´lise de Sensibilidade
a

33. Em s´
ıntese
Teorema
1 O conjunto T de todos os valores de c para os quais o custo ´timo ´
o e
finito ´ convexo.
e
2 A fun¸˜o custo ´timo G (c) ´ uma fun¸˜o concava de c em T .
ca o e ca
3 Se para um determinado valor c, a solu¸˜o primal ´tima ´ unica,
ca o e´
ent˜o G ´ linear nas vizinhan¸as de c e seu gradiente ´ dado por x ∗ .
a e c e
Alexandre Salles da Cunha An´lise de Sensibilidade
a