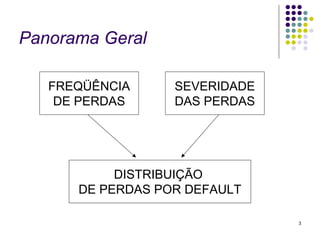
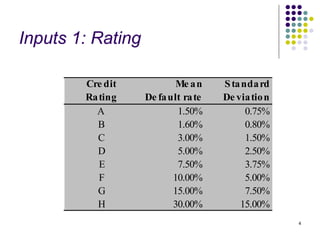
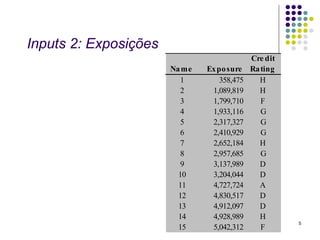
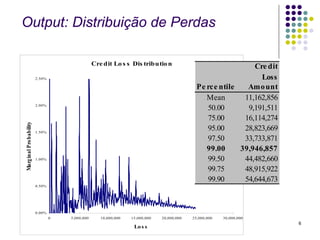
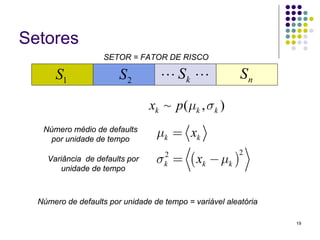
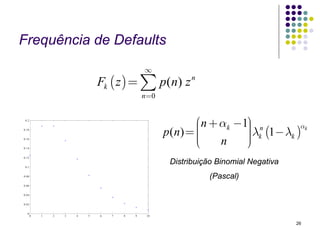
Este documento discute modelos para avaliar o risco de crédito. Primeiramente, aborda um modelo com taxas de inadimplência constantes em um único setor, analisando a frequência e severidade das perdas. Em seguida, apresenta um modelo com taxas variáveis em múltiplos setores, considerando como esses fatores afetam a análise de risco. Por fim, fornece inputs e outputs para exemplificar os cálculos desses modelos.

1. Modelos para Risco
de Crédito 2:
Credit Risk +
Análise de Risco (10)
R.Vicente
1

2. Resumo
Introdução
Taxas de default constantes e setor único
Freqüência de Defaults
Severidade das Perdas
Taxas de default variáveis e múltiplo setor
Freqüência de Defaults
Severidade das Perdas
Bibliografia
2

3. Panorama Geral
FREQÜÊNCIA SEVERIDADE
DE PERDAS DAS PERDAS
DISTRIBUIÇÃO
DE PERDAS POR DEFAULT
3

4. Inputs 1: Rating
Cre dit Me a n S ta nda rd
Ra ting De fa ult ra te De via tio n
A 1.50% 0.75%
B 1.60% 0.80%
C 3.00% 1.50%
D 5.00% 2.50%
E 7.50% 3.75%
F 10.00% 5.00%
G 15.00% 7.50%
H 30.00% 15.00%
4

5. Inputs 2: Exposições
Cre dit
Na me Ex po sure Ra ting
1 358,475 H
2 1,089,819 H
3 1,799,710 F
4 1,933,116 G
5 2,317,327 G
6 2,410,929 G
7 2,652,184 H
8 2,957,685 G
9 3,137,989 D
10 3,204,044 D
11 4,727,724 A
12 4,830,517 D
13 4,912,097 D
14 4,928,989 H
5
15 5,042,312 F

6. Output: Distribuição de Perdas
Cre dit Lo s s Dis tributio n Cre dit
2.50% Loss
Pe rce ntile Amo unt
Mean 11,162,856
2.00%
50.00 9,191,511
75.00 16,114,274
Marg inal Pro bability
1.50%
95.00 28,823,669
97.50 33,733,871
99.00 39,946,857
1.00% 99.50 44,482,660
99.75 48,915,922
99.90 54,644,673
0.50%
0.00%
0 5,000,000 10,000,000 15,000,000 20,000,000 25,000,000 30,000,000
6
Lo s s

7. TAXAS DE DEFAULT
CONSTANTES E SETOR
ÚNICO
7

8. Freqüência de Defaults
Suponhamos uma carteira contendo N contrapartes.
Qual é a probabilidade p ( n) de n defaults em uma janela de
tempo especificada ?
N
Introduzamos a função auxiliar F ( z ) = ∑ p ( n) z n
n=0
Seja q j = Probabilidade de default de j na janela , assumindo que:
a) defaults são eventos independentes;
b) taxas não variam no tempo, teremos:
N N
F ( z ) = ∏ ⎢⎡(1− q j ) + q j z ⎥⎤ = ∏ ⎡⎣1 + q j ( z −1)⎤⎦
j =1
⎣ ⎦ j=1
8

9. Freqüência de Defaults
N
F ( z ) = ∏ ⎡⎣1 + q j ( z −1)⎤⎦
j =1
N
ln F ( z ) = ∑ ln ⎡⎣1 + q j ( z −1)⎤⎦
j =1
Assumindo que 0 < qj 1 , utilizamos ln (1 + ε) ≈ ε e obtemos:
N
ln F ( z ) = ( z −1) ∑ q j
j =1
⎡ N ⎤
F ( z ) = exp ⎢⎢( z −1) ∑ q j ⎥⎥
⎢⎣ j =1 ⎥⎦ 9

10. Freqüência de Defaults
N
Identificando o número médio de defaults μ = ∑q
j =1
j :
F ( z ) = e−μ e zμ
Expandindo em série de Taylor:
∞
e−μ μ n n ∞
F ( z) = ∑ z = ∑ p ( n) z n
n=0 n! n=0
Lembrando da definição da função auxiliar.
e−μ μ n
p ( n) =
n! 10

11. Severidade dos Defaults
Para cada contraparte j.
A exposição a risco de crédito é a perda incorrida em um default.
L j = Lν j
A perda esperada é a perda agregada esperada dada por:
λ j = L j μ j = Lν j μ j = Lε j
Probabilidade de
default de acordo
com a
classificação de
crédito 11

12. Severidade dos Defaults
As exposições são agrupadas em bandas:
Lν1 Lν2 Lν3 Lν4 ... Lνm νa ∈
Cada banda com uma perda esperada associada:
εa = ν a μa 1 ≤ a ≤ m
O número esperado de defaults em cada banda dado por :
εj
μa = ∑
j:ν j =ν a νj 12

13. Severidade dos Defaults
Introduzindo uma função geratriz para as perdas agregadas:
∞
G ( z ) = ∑ p (nL) z n
n=0
Assumindo as bandas são independentes (as exposições são
independentes):
m
G ( z ) = ∏ Ga ( z )
a=1
Tratando cada banda como uma carteira :
∞
e−μa μa nνa
∞ n
Ga ( z ) = ∑ p(n) z nνa =∑ z =e−μa +μa z ν a
n=1 n=1 n! 13

14. Severidade dos Defaults
∞ ∞ −μa
e μ nνan
Ga ( z ) = ∑ p(n) z nν a
=∑ z =e
a−μa +μa z ν a
n=1 n=1 n!
m m
G ( z ) = ∏ Ga ( z ) = ∏ e −μa +μa z ν a
a =1 a =1
⎡ m m ⎤
= exp ⎢−∑ μa + ∑ μa z ⎥
νa
⎢⎣ a=1 a =1
⎥⎦
14

15. Severidade dos Defaults
Derivadas n-ésimas da função geratriz em z=0 fornecem as
probabilidades p(n) ∞ n
1 d G( z)
G ( z ) = ∑ p(lL) z l
n
= p (nL)
l =0 n ! dz z =0
1 d nG ( z ) 1 dn ⎡ m m ⎤
= exp ⎢−∑ μa + ∑ μa z ⎥
νa
n ! dz n
n ! dz n ⎢⎣ a=1 a =1
⎥⎦
z =0 z =0
1 d n−1 d m
=
n ! dz n−1
G( z)
dz
∑ μa z νa
z =0 z =0 a =1
1 n−1 ⎜n −1⎞ d n−k −1
⎛ ⎟ d k +1 m
= ∑⎜ ⎟
⎟ G ( z ) k +1 ∑ μa z νa
⎜ k ⎠ dz n−k −1
n ! k =0 ⎝ ⎟ dz
z =0 z =0 a =1
15

16. Severidade dos Defaults
d n−k −1G ( z )
n−k −1
= (n − k −1)! p ((n − k −1)! L)
dz z =0
d k +1 m ⎧μa (k + 1)!, se ∃a : ν a = k + 1
⎪
∑ μa z = ⎪
νa
⎨
dz k +1 z =0 a =1
⎪
⎪
⎩ 0, cc
1 n−1 ⎛n −1⎞
⎟
⎜
p (nL) = ∑
n ! k =0
⎜
⎜ k ⎠
⎝
⎟(n − k −1)!(k + 1)!μa p((n − k −1) L)
⎟
⎟
∃a:ν a = k +1
16

17. Severidade dos Defaults
⎛ ⎞
1 n−1 ⎜n −1⎟(n − k −1)!(k + 1)!μ p ((n − k −1) L)
p (nL) = ∑
n ! k =0
⎜
⎜ k ⎠
⎝
⎟
⎟
⎟ a
∃a:ν a = k +1
ν a μa εa
p (nL) = ∑ p((n − ν a ) L) = ∑ p ((n − ν a ) L)
a:ν a ≤n n a:ν a ≤n n
⎡ m ⎤
p(0) = exp ⎢−∑ μa ⎥
⎢⎣ a=1 ⎥⎦ 17

18. TAXAS DE DEFAULT
VARIÁVEIS E MÚLTIPLOS
SETORES
18

19. Setores
SETOR = FATOR DE RISCO
S1 S2 Sk Sn
xk ~ p (μk , σk )
Número médio de defaults
por unidade de tempo
μk = xk
σ = ( xk − μk )
2 2
Variância de defaults por
k
unidade de tempo
Número de defaults por unidade de tempo = variável aleatória
19

20. Volatilidades
Volatilidades e taxas de default dependem primordialmente da qualidade da
contraparte. Volatilidades e taxas de cada setor são obtidas a partir de dados
para cada rating.
μa FATOR DE
x =
a x RISCO μ =
μk
k k μ ∑a
a
( xa − μa )
Cre dit Me a n S ta nda rd 2
Ra ting De fa ult ra te De via tio n σ =
2
a
A 1.50% 0.75%
⎛ μa xk ⎞ ⎛ μa ⎞ 2
B 1.60% 0.80% 2 2
C 3.00% 1.50% ⎜
= ⎜
⎜ μ − μa ⎟
⎟
⎟ = ⎜ ⎟ σk
⎜ ⎟
⎜μ ⎠ ⎟
D 5.00% 2.50%
⎝ k
⎟
⎠ ⎝ ⎟
k
E 7.50% 3.75%
F 10.00% 5.00%
G 15.00% 7.50%
σk
H 30.00% 15.00% σa = μa
μk 20

21. Volatilidades
μa σk
μk = ∑ μa xa = xk σa = μa
μk μk
a
σk
∑ σa = μ ∑μ
Cre dit Me a n S ta ndard
Ra ting De fa ult ra te De via tio n
a = σk
A 1.50% 0.75% a a
k
B 1.60% 0.80%
C 3.00% 1.50%
D 5.00% 2.50% Ex: SETOR = A+B+H
E 7.50% 3.75%
F 10.00% 5.00% μsetor = μ A + μB + μH
G 15.00% 7.50%
H 30.00% 15.00% = 1,5% + 1, 6% + 30% = 33, 2%
σ setor = σ A + σB + σH
= 0, 75% + 0,8% + 15 = 16,55%
21

22. Número de Defaults com Taxa de
Defaults Estocástica
n
F ( z ) = ∏ Fk ( z ) SETORES
k =1 INDEPENDENTES
Fk ( z xk = x) = e
x( z−1)
∞
Fk ( z ) = ∫ dx Fk ( z xk = x ) f ( x )
x=0
∞
x( z −1)
= ∫ dx e f ( x)
x=0
22

23. Taxa de Defaults Estocástica:
Distribuição Gama ∞
Fk ( z )= ∫ dx e ( ) f ( x)
x z −1
−
x x=0
1
f ( x) = α e xα−1 β
β Γ(α ) ∞
μ = αβ σ 2 = αβ 2
Γ(α ) = ∫ dx e− x x α−1
x =0
1 0.2 0.045
0.9
0.8
0.18
0.16
α=5 0.04
0.035
α = 100
0.7
β =1 β =1
0.14
0.03
0.6
0.12
α = β =1
0.025
0.5
0.1
0.02
0.4
0.08
0.3 0.015
0.06
0.2 0.01
0.04
0.1
0.02 0.005
0
0 1 2 3 4 5 6
0 0
0 2 4 6 8 10 12 14 70 80 90 100 110 120 130 140
μk
2
σk
2
PARA O SETOR k αk = 2 βk =
σk μk 23

24. Taxa de Defaults Estocástica
∞ ∞ x
1 −
x( z −1) x( z−1)
Fk ( z ) = ∫ dx e f ( x) = ∫ dx e e x α−1β
x=0 x =0
β α Γ(α )
∞ x
1 xz − x−
∫ dx e x α−1
β
= α =
β Γ(α ) x=0 ⎜
⎜
⎛ 1⎞
y =− x⎜ z−1− ⎟
⎟
⎟
⎟
⎝ β⎠
∞
1 1
∫
−y α−1
= α
dy e y = α
⎛ 1 ⎞ ⎛ 1 ⎞
β Γ(α ) ⎜1 + − z ⎟
α
⎜ ⎟
⎟
y =0
β ⎜1 + − z ⎟
α⎜
⎟
⎟
⎜ β
⎝ ⎠ Γ (α ) ⎜
⎝ β ⎠
24

25. Taxa de Defaults Estocástica
αk
1 ⎛ 1− λk ⎞
⎟
Fk ( z ) = = ⎜ ⎜ ⎟
⎟
⎞ λk = ββ ⎜1− λk z ⎠
⎟
αk
⎛ ⎝
βk k ⎜1 + − z ⎟
k
α 1
⎜ ⎟
⎟
1+ k
⎜ β
⎝ ⎟
⎠
k
αk
⎛ 1− λk ⎞
⎟
Fk ( z ) = ⎜
⎜ ⎟
⎟
⎜1− λ z ⎠
⎝ k
⎟
αk
⎡ αk (αk −1) 2 2 ⎤
= (1− λk ) ⎢1 + zαk λk + λk z + ⎥
⎢ 2! ⎥
⎣ ⎦
∞ ⎛
⎜ n + αk −1⎞ n n
⎟
= (1− λk ) ∑ ⎜
αk
⎟λk z
⎟
n=0
⎜
⎝ n ⎟
⎠ 25

26. Frequência de Defaults
∞
Fk ( z ) = ∑ p (n) z n
n=0
0.2
⎛n + αk −1⎞ n
⎟λ (1− λ )αk
⎜
p ( n) = ⎜ ⎟ k
⎟
0.18
0.16
⎜
⎝ n ⎟
⎠
k
0.14
0.12
0.1
Distribuição Binomial Negativa
0.08 (Pascal)
0.06
0.04
0.02
0
0 1 2 3 4 5 6 7 8 9 10
26

27. Bibliografia
•Crouhy M. Galai D. e Mark R., A comparative analysis of current credit risk
models, Journal of Banking and Finance 24 (2000) 59-117.
•Jorion P., Value at Risk, Irwin, 1997.
• Saunders A., Credit Risk Measurement, John Wiley, 1999
•CreditRisk+,CSFB,1997 (http://www.csfb.com/creditrisk/)
Leitura Complementar
Basle Committee on Banking Supervision, Credit Risk Modelling:
Current Practices and Applications, April 1999. (www.bis.org)
27