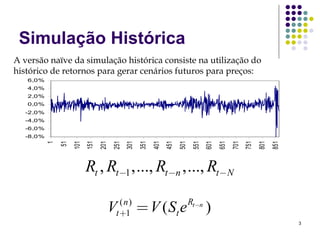
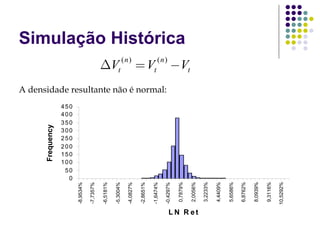
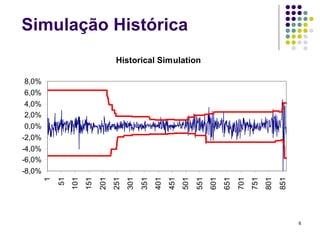
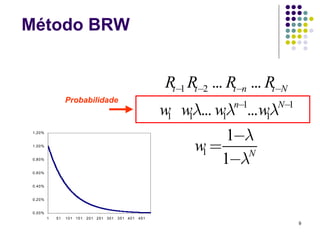
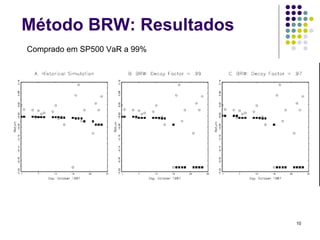
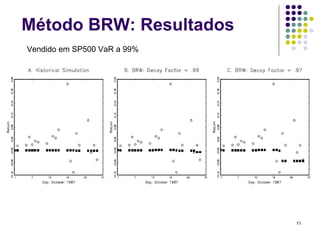
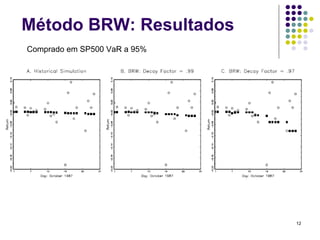
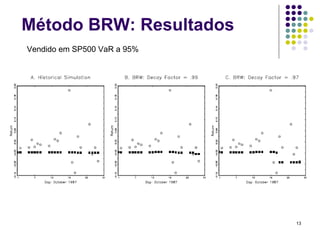
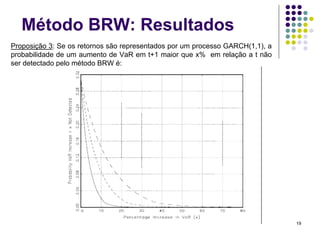
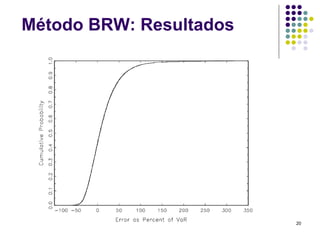
O documento discute métodos de simulação histórica para estimar Value at Risk (VaR). A simulação histórica naïve usa o histórico de retornos para gerar cenários futuros. O método BRW atribui pesos diferentes aos cenários históricos. O método de Hull-White normaliza os retornos usando estimativas de volatilidade GARCH/EWMA.

1. Simulação Histórica
Análise de Risco (6)
R.Vicente
1

2. Resumo
Simulação Histórica
Método BRW (Boudoukh-Richardson-Whitelaw)
Volatilidade Ajustada (Método Hull-White)
Bibliografia
2

3. Simulação Histórica
A versão naïve da simulação histórica consiste na utilização do
histórico de retornos para gerar cenários futuros para preços:
6,0%
4,0%
2,0%
0,0%
-2,0%
-4,0%
-6,0%
-8,0%
1
51
101
151
201
251
301
351
401
451
501
551
601
651
701
751
801
851
Rt , Rt−1 ,..., Rt−n ,..., Rt−N
V (n)
t +1 = V ( St e Rt−n
)
3

4. Frequency
150
200
250
300
350
400
450
0
50
100
-8,9534%
-7,7357%
-6,5181%
ΔVt
-5,3004%
(n)
-4,0827%
-2,8651%
= Vt
-1,6474%
A densidade resultante não é normal:
(n)
-0,4297%
0,7879%
Simulação Histórica
−Vt
2,0056%
LN R et
3,2233%
4,4409%
5,6586%
6,8762%
8,0939%
9,3116%
10,5292%
4

5. Simulação Histórica
A função distribuição cumulativa empírica é dada por:
N
1
∑1
Massa de
P ( x; t , N ) = {ΔVt ( j ) ≤ x} P&L até x
N j =1
VaRα = inf (ΔV ∈ {ΔV (1) ,..., ΔV ( N ) }| P(ΔV ; t , N ) ≥ α )
inf
VaRα = sup (ΔV ∈ {ΔV (1) ,..., ΔV ( N ) }| P(ΔV ; t , N ) ≤ α )
sup
(VaRα + VaRα )
inf sup
VaRα =
2 5

6. Simulação Histórica
Historical Simulation
8,0%
6,0%
4,0%
2,0%
0,0%
-2,0%
-4,0%
-6,0%
-8,0%
1
51
101
151
201
251
301
351
401
451
501
551
601
651
701
751
801
851
6

7. Prós e Contras
Prós Contras
Não é necessário estimar Cenários têm mesmo peso (1/N).
volatilidades ou correlações.
Nenhuma hipótese prévia Cenários com volatilidades
sobre a densidade dos diferentes são utilizados
retornos é necessária. simultaneamente.
7

8. Método BRW
Boudoukh,Rishardson,Whitelaw
A função distribuição cumulativa empírica é dada por:
N
P( x; t , λ, N ) = ∑ wt− j 1{ΔV ( j ) ≤x}
j =1
⎛ 1− λ ⎞ j−1 N
⎟λ ⇒ ∑ w = 1 , w
wt− j =⎜
⎜ ⎟
⎟ t − j−1 = λ wt − j
⎜1− λ N ⎠
⎝ j =1
t− j
VaRα = inf (ΔV ∈ {ΔV (1) ,..., ΔV ( N ) }| P(ΔV ; λ, t , N ) ≥ α )
inf
VaRα = sup (ΔV ∈ {ΔV (1) ,..., ΔV ( N ) }| P(ΔV ; λ, t , N ) ≤ α )
sup
8

9. Método BRW
Rt−1 Rt−2 ... Rt−n ... Rt−N
Probabilidade
n− N−
w wλ... wλ ...wλ
1 1 1 1
1 1
1,20%
1−λ
1,00%
w=
1−λ
1 N
0,80%
0,60%
0,40%
0,20%
0,00%
1 51 101 151 201 251 301 351 401 451
9

10. Método BRW: Resultados
Comprado em SP500 VaR a 99%
10

11. Método BRW: Resultados
Vendido em SP500 VaR a 99%
11

12. Método BRW: Resultados
Comprado em SP500 VaR a 95%
12

13. Método BRW: Resultados
Vendido em SP500 VaR a 95%
13

14. Método BRW: Resultados
Proposição 1: O VaR aumenta somente após pelo menos uma
violação, ou seja, a probabilidade de o VaR aumentar de um período
ao próximo é de 1- α
R > VaR (t ) ⇒VaR (t + 1) ≥ VaR (t )
t α
sup sup
α α
sup
t-1
t
14

15. Método BRW: Resultados
Proposição 2: Se os retornos são descritos por um processo
GARCH(1,1) e a volatilidade estiver em seu nível médio σ , então:
P {VaRα (t + 1) > VaRα (t )} = 31, 73%
Demonstração:
Seja o processo GARCH(1,1) definido por:
Rt = σt εt
σt2 = α0 + α1 Rt2 1 + β1σt2−1
−
15

16. Método BRW: Resultados
Demonstração:
A volatilidade que é ponto fixo da dinâmica no longo prazo é:
α0
σ =
2
1− α1 − β1
Quando σt = σ , σt +1 > σt se e somente se
α0 + α1 Rt2 + β1σt2 > σt2
α0 + α1σt2ε 2 + β1σt2 > σt2
α0 + β1σ 2 − σ 2
> ε2 ⇒ ε2 > 1
α1σ 2
16

17. Método BRW: Resultados
Demonstração:
α0 + α1 Rt2 + β1σt2 > σt2
α0 + α1σt2ε 2 + β1σt2 > σt2
α0 + β1σ 2 − σ 2
> ε2 ⇒ ε2 > 1
α1σ 2
P (ε 2 > 1) = P(ε > 1) + P(ε < −1) = 2Φ(−1) 0,3173
QED
17

18. Método BRW: Resultados
Proposição 3: Se os retornos são representados por um processo
GARCH(1,1), a probabilidade de um aumento de VaR em t+1 maior
que x% em relação a t não ser detectado pelo método BRW é:
⎧
⎪ ΔVaRα
⎪ ⎫
⎪ ⎧
⎪2Φ( z ) − α, 0 < x < k (α1 , α )
P⎨ > x% , no detection⎪
⎬ ⎪
⎨
⎪VaRα (t )
⎪
⎩ ⎪
⎪
⎭ ⎪
⎪
⎩ Φ( z ), x ≥ k (α1 , α )
x2 + 2 x
z = − 1+
α1
k (α1 , α ) = 1− α1 + α1 ⎡⎢⎣Φ−1 (α )⎤⎥⎦
2
18

19. Método BRW: Resultados
Proposição 3: Se os retornos são representados por um processo GARCH(1,1), a
probabilidade de um aumento de VaR em t+1 maior que x% em relação a t não
ser detectado pelo método BRW é:
19

20. Método BRW: Resultados
20

21. Método de Hull-White
São realizadas estimativas GARCH ou EWMA de volatilidades e
os retornos são normalizados.
5,0
3,0
1,0
-1,0
-3,0
-5,0
1 51 101 151 201 251 301 351 401 451 501 551 601 651 701 751 801 851
Rt Rt−1 Rt−n Rt−N
, ,..., ,...,
σt σt−1 σ t −n σt − N
Rt−n
σt +1
σt−n
V (n)
t +1 = V ( St e ) 21

22. Bibliografia
• Jorion P., Value at Risk, Irwin, 1997.
• RiskMetrics Technical Document (www.riskmetrics.com);
•Pritsker M., The Hidden Dangers of Historical Simulation.
Leituras Complementares
Hull, J. e White, A., Incorporating Volatility Updating into the Historical
Simulation Method for Value at Risk
22