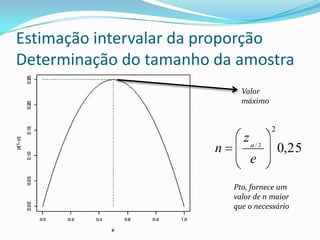
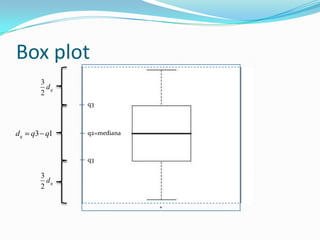
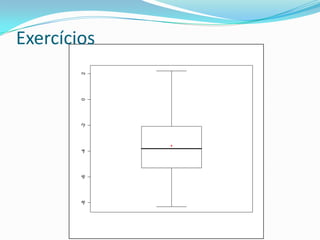
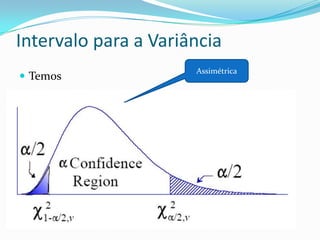
O documento descreve os tópicos abordados na última aula da autora Caroline Godoy sobre estatística. Os principais pontos incluem estimativa pontual e intervalar da média populacional, teorema central do limite, distribuição da média amostral, determinação do tamanho da amostra e intervalos de confiança.

1. Caroline Godoy
Turma : Sistemas de Informação

2. Última aula
 Aula 1:
 Estimativa Pontual para a Média ;

3. Última aula
 Aula 1:
 Estimativa Pontual para a Média ;
 Teorema Central do Limite;
2
x~N ;
n

4. Última aula
 Aula 1:
 Estimativa Pontual para a Média ;
 Teorema Central do Limite;
 Distribuição amostral da média com variância
conhecida;
Transformando xbarra para z
padronizado
Usando o teorema central
do limite: 2
x~N ;
n
Z ~ N (0;1)

5. Última aula
 Aula 1:
 Estimativa Pontual para a Média ;
 Teorema Central do Limite;
 Distribuição amostral da média com variância
conhecida;
 Intervalo de confiança com variância conhecida;

6. Última aula
 Aula 1:
 Estimativa Pontual para a Média ;
 Teorema Central do Limite;
 Distribuição amostral da média com variância
conhecida;
 Intervalo de confiança com variância conhecida;
 Determinação do tamanho da amostra
Onde e é o erro determinado pelo
pesquisador

7. Última aula
 Aula 1:
 Estimativa Pontual para a Média ;
 Teorema Central do Limite;
 Distribuição amostral da média com variância
conhecida;
 Intervalo de confiança com variância conhecida;
 Determinação do tamanho da amostra
 Distribuição amostral da média e intervalo de confiança
com variância desconhecida;
1º ~tn-1
E t /2
n

8. Estimação por ponto da proporção
 O estimador pontual para p (proporção) é definido
como:
X
ˆ
p
n
 onde X é a característica considerada, n é o tamanho
da amostra e X ~ bin(n; p) ;
 Utilizando o TCL, para n grande:
p(1 p)
ˆ
p ~ N p;
n

9. Estimação intervalar da proporção
 Então utilizando o intervalo já visto para a média,
porém utilizando proporção tem-se:
ˆ ˆ
p(1 p)
ˆ
IC( p; ) : p z /2
n

10. Estimação intervalar da proporção
Determinação do tamanho da amostra
 Do intervalo,
ˆ ˆ
p(1 p)
ˆ
IC( p; ) : p z /2
e
n
 ou seja, Não conheço => amostra
piloto
ˆ ˆ
p(1 p) 2 ˆ ˆ
p(1 p)
e z /2 n z
n /2
e2

11. Estimação intervalar da proporção
Determinação do tamanho da amostra
Valor
máximo
2
z
n /2
0,25
e
Pto, fornece um
valor de n maior
que o necessário

12. Estimação intervalar para amostras
não normais e grandes
 Utilizar a mesma teoria para dados normais devido ao
Teorema central do limite:
Sx
X z /2
n

13. Metodologia e Condições
 Se o interesse é construir intervalos para a média
populacional de uma determinada característica de
interesse:
Método Condições
Use Distribuição • Variância conhecida e distribuição da característica em estudo
Normal P. (Z) de distribuição Normal
• Variância conhecida e n ≥ 30
Use a Distribuição t- • Variância desconhecida e distribuição da característica da
Student população, Normal
• Variância desconhecida e n ≤ 30
Use Distribuição • Distribuição não normal e com n grande
Normal P. (Z)
Use métodos não- • População não normal e amostras pequenas
paramétricos

14. Como testar a normalidade?
 Faça um gráfico para analisar a assimetria de valores e
valores atípicos;
 Para a maioria dos casos a distribuição t-Sudent pode
ser utilizada para amostras maiores que 30 a menos
que haja um valor atípico ou assimetria muito
forte

15. Box plot
 Utilizado para verificar o comportamento da
distribuição dos dados;
 Necessário: Mediana e Quantil 1 e Quantil 3
 Q(0,25): 1º Quartil;
 Q(0,50): Mediana;
 Q(0,75): 3º Quartil. 50% das
observações
x(1) q1 q2 q3 x(n)

16. Box plot
3
dq
2
q3
dq q3 q1 q2=mediana
q3
3
dq
2
*

17. Exercícios

18. Exercícios

19. Apresentação dos dados
• Portal Action – Software Livre de conexão R + Excel

20. Exercícios
2
0
-2
-4
-6
-8

21. Exercícios
 Para estimar o rendimento semanal de operários de
construção de uma grande cidade, um sociólogo
seleciona uma amostra aleatória de 75 operários. A
média amostral é dada por 427 reais e o desvio padrão
da amostra é 15 reais. Determine um intervalo de
confiança para considerando coeficientes de
confiança de 0,9 e 0,95;

22. Exercícios
 Para estimar o rendimento semanal de operários de
construção de uma grande cidade, um sociólogo
seleciona uma amostra aleatória de 75 operários. A
média amostral é dada por 427 reais e o desvio padrão
da amostra é 15 reais. Determine um intervalo de
confiança para considerando coeficientes de
confiança de 0,9 e 0,95;

23. Intervalo para a Variância
 Muitos processo exigem a estimação da variabilidade.
 Ex: controle de qualidade
 Partindo que
(n 1) S 2 2
2
~ Xn 1

24. Intervalo para a Variância
Assimétrica
 Temos

25. Intervalo para a Variância
2
 Como a distribuição é assimétrica o IC para não é da
2
forma S e e deve ser representado por:
(n 1) S 2
P X 12 2
2
X2
(n 1) S 2 2 (n 1) S 2
P 2
X2 X 12

26. Exercícios
 Um fabricante de esferas para rolamento desenvolveu
um novo método de produção mais barato. Ele
necessita de produtos mais baratos porém com
qualidade consistente. (menor variab.). Para analisar a
variabilidade do produto ele selecionou 15 esferas
obtendo os seguintes diâmetros em mm.
29,8 29,8 29,6 29,8 29,9 30,0 29,9 29,9 30,0 29,7
30,1 29,9 29,9 29,9 30,8

28. Conceitos
 Vimos que podemos tirar informações dos parâmetros
de uma de uma população através de uma amostra,
porém na maioria das vezes precisamos comparar esses
valores com outros já pré estabelecidos;
 Para isso existem os testes de hipóteses que fornecem
uma metodologia para verificar se os dados amostrais
trazem evidências que apoiam ou não uma hipótese
formulada.

29. Conceitos - Exemplo
Hipótese Científica:
H0: O novo medicamento não é melhor que o medicamento tradicional.
H1: O novo medicamento é melhor que o medicamento tradicional.

30. Conceitos – Exemplo cont.
n
Variável de interesse
Hipótese Estatística:
H0: p≤0,4 (O medicamento novo não é melhor que o tradicional)
H1: p>0,4 (O medicamento novo é melhor que o tradicional)

31. Conceitos – Exemplo cont.
• Regra de decisão:
Rejeita H0 se Y ≥ 9
Não rejeita H0 se Y < 9
• Testar uma hipótese estatística significa estabelecer uma
regra que nos permita, com base na informação da amostra,
decidir pela rejeição ou não de H0.
• Região de Rejeição ou Região Crítica
RC = {9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20} : região crítica
RCc = {0, 1, 2, 3, 4, 5, 6, 7, 8}: região de aceitação de H0

32. Conceitos – Exemplo cont.
• Na decisão pela rejeição ou não da hipótese nula pode-se
cometer 2 tipos de erros:
Decisão baseada Situação na população
na amostra H0 Verdadeira H0 Falsa
Não Rejeitar H0 Decisão correta Erro Tipo II
Rejeitar H0 Erro Tipo I Decisão correta
• Erro Tipo I: Dizer que o medicamento novo é melhor que o
tradicional, quando na verdade não é;
• Erro Tipo II: Dizer que o medicamento novo não é melhor
que o tradicional, quando na verdade é melhor.

33. Conceitos – Exemplo cont.
• Na decisão pela rejeição ou não da hipótese nula pode-se
cometer 2 tipos de erros:
Decisão baseada Situação na população
na amostra H0 Verdadeira H0 Falsa
Não Rejeitar H0 Decisão correta Erro Tipo II
Rejeitar H0 Erro Tipo I Decisão correta
• Erro Tipo I: Dizer que o medicamento novo é melhor que o
tradicional, quando na verdade não é;
• Erro Tipo II: Dizer que o medicamento novo não é melhor
que o tradicional, quando na verdade é melhor.

34. Probabilidades de erros
• O maior valor do erro tipo I é chamado de nível de
significância de um teste (prob. máxima que aceitamos de
ocorrer o risco do erro), denotado por:
P(erro tipo I ) P(rejeitar H 0 | H0 é verdadeira)
• A probabilidade de ocorrer o erro tipo II é denotada por:
P(erro tipo II ) P(não rejeitar H 0 | H0 é falsa)
• Em geral, o erro tipo I é mais sério que o erro tipo II,
portanto escolhe-se controlar e escolhe-se um teste tal
que seja o menor possível.

35. Próxima aula
• Teste de hipóteses