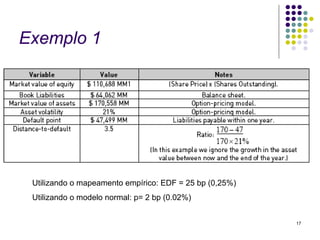
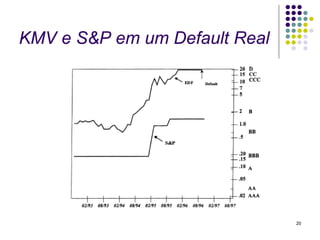
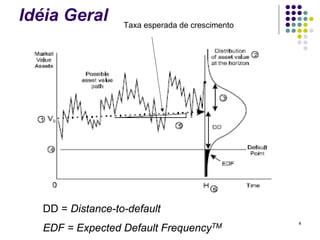
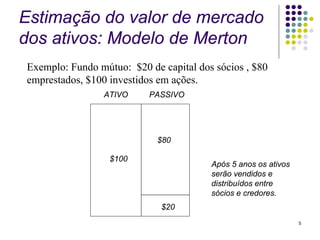
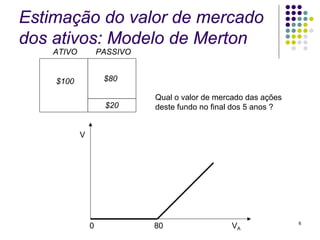
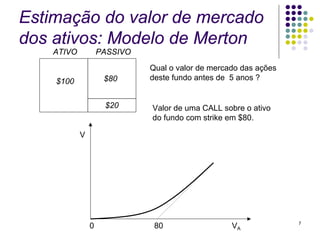
O documento resume o modelo KMV de análise de risco de crédito, que calcula a probabilidade de default de um ativo usando a distância-para-default. A distância-para-default mede a diferença entre o valor de mercado dos ativos e o ponto de default, ajustado pela volatilidade. A probabilidade de default é então calculada usando uma curva empírica que corrige os efeitos do processo estocástico assumido.

1. Modelos para Risco
de Crédito 3:
KMV
Análise de Risco (11)
R.Vicente
1

2. Resumo
Introdução
Estimação do valor de mercado e volatilidade
dos ativos
Cálculo da Distância-para-default
Cálculo da Probabilidade de Default
Bibliografia
2

3. Principal Diferença
KMV Credit Risk+ e
Credit Metrics
Probabilidade de default Probabilidade de default
calculada para cada ativo determinada pela taxa
média para cada
classificação de crédito
3

4. Idéia Geral Taxa esperada de crescimento
DD = Distance-to-default
4
EDF = Expected Default FrequencyTM

5. Estimação do valor de mercado
dos ativos: Modelo de Merton
Exemplo: Fundo mútuo: $20 de capital dos sócios , $80
emprestados, $100 investidos em ações.
ATIVO PASSIVO
$80
$100
Após 5 anos os ativos
serão vendidos e
distribuídos entre
sócios e credores.
$20
5

6. Estimação do valor de mercado
dos ativos: Modelo de Merton
ATIVO PASSIVO
$100 $80
Qual o valor de mercado das ações
$20 deste fundo no final dos 5 anos ?
V
6
0 80 VA

7. Estimação do valor de mercado
dos ativos: Modelo de Merton
ATIVO PASSIVO
Qual o valor de mercado das ações
$100 $80 deste fundo antes de 5 anos ?
$20 Valor de uma CALL sobre o ativo
do fundo com strike em $80.
V
7
0 80 VA

8. Estimação do valor de mercado
dos ativos: Modelo de Merton
VE = VAN (d1 ) − e XN (d2 )
rT
VA VA
σE = σA Δ = σA N (d1 )
VE VE
⎛VA ⎞ ⎜ ⎛ 2 ⎞
⎜ ⎟ ⎟ + ⎜r + σA ⎟T
ln ⎜ ⎟ ⎜ ⎟
⎜X ⎠ ⎜
⎝ 2⎠⎟
⎟
⎝
d1 =
σA T
d2 = d1 − σA T 8

9. Distância para Default
⎡ Valor de Mercado⎤ ⎡ Ponto ⎤
⎢ ⎥−⎢ ⎥
⎡ Distancia ⎤ ⎢ dos Ativos ⎥ ⎢de Default⎥
⎢ ⎥ = ⎢⎣ ⎥⎦ ⎢⎣ ⎥⎦
⎢ para Default⎥ ⎡ Valor de Mercado⎤ ⎡ Volatilidade ⎤
⎢⎣ ⎥⎦ ⎢ ⎥⎢ ⎥
⎢ dos Ativos ⎥ ⎢ dos Ativos ⎥
⎢⎣ ⎥⎦ ⎢⎣ ⎥⎦
Ponto de Default = STRIKE (X)
= Dívida de Curto Prazo + ½ Divida de Longo Prazo
9

10. Probabilidade de Default
⎡V t ≤ X V 0 = V ⎤
pt = Pr ⎢ A
⎣ t A A⎥
⎦
⎡lnV t ≤ ln X V 0 = V ⎤
= Pr ⎢
⎣ A t A A⎥
⎦
10

11. Probabilidade de Default
Assumindo uma dinâmica browniana geométrica:
⎛ 2 ⎞
σA ⎟
lnVA = lnVA + ⎜μA − ⎟ t + σA t ε
t
⎜
⎜ ⎟
⎜
⎝ 2⎠⎟
A probabilidade que se deseja calcular é equivalente à probabilidade da
Call com strike Xt “virar pó” em t :
⎡ ⎛ σA ⎞
2 ⎤
pt = Pr ⎢⎢lnV + ⎜μ − ⎟ t + σ t ε ≤ ln X ⎥
⎜ ⎟
A ⎜ A
⎜ ⎟
⎟ A t⎥
⎢⎣ ⎝ 2⎠ ⎥⎦ 11

12. Probabilidade de Default
⎡ ⎛ σA ⎞
2 ⎤
pt = Pr ⎢⎢lnV + ⎜μ − ⎟ t + σ t ε ≤ ln X ⎥
⎜ ⎟
A ⎜ A
⎜ ⎟
⎟ A t⎥
⎢⎣ ⎝ 2⎠ ⎥⎦
Rearranjando:
⎡ ⎛V ⎞ ⎛ σA ⎞
2 ⎤
⎜ ⎟ + ⎜μ − ⎟ t
⎢ ln ⎜ A ⎟ ⎟ ⎥
⎟ ⎜ A
⎢ ⎜X ⎟
⎢ ⎝ ⎜ t⎠ ⎜
⎜
⎝ 2⎟⎟
⎠
⎥
pt = Pr ⎢ ≥ ε⎥⎥
⎢ σA t ⎥
⎢ ⎥
⎢⎣ ⎥⎦
12

13. Probabilidade de Default
Como ε ´é um choque normal :
⎡ ⎛V ⎞ ⎛ σA ⎞ ⎤⎥
2
⎢ ln ⎜ A ⎟ + ⎜μ − ⎟ t
⎜ ⎟ ⎜ A ⎟ ⎥
⎢ ⎜X ⎟
⎜ t⎠⎟ ⎜
⎜ ⎟
⎟
⎢− ⎝ ⎝ 2⎠ ⎥
pt =N ⎢ ⎥
⎢ σA t ⎥
⎢ ⎥
⎢⎣ ⎥⎦
13

14. Ligando Probabilidade de
Default e Distância para Default:
⎡ ⎛V ⎞ ⎛ σA ⎞ ⎤⎥
2
⎢ ln ⎜ A ⎟ + ⎜μ − ⎟ t
⎜ ⎟ ⎜ ⎟ ⎥
⎢ ⎜X ⎟
⎜ t⎠⎟ ⎜ A
⎜ ⎟
⎟
⎢− ⎝ ⎝ 2⎠ ⎥
pt =N ⎢ ⎥
⎢ σA t ⎥
⎢ ⎥
⎢⎣ ⎥⎦
DD é o número de desvios padrão entre o valor de mercado dos
ativos e o Ponto de Default:
⎛V ⎞ ⎛ 2 ⎞
⎜ A ⎟ + ⎜μ − σA ⎟ t
⎜
ln ⎜ ⎟ ⎟ ⎜ ⎟
⎟
⎜ Xt ⎠ ⎜
⎜ A 2⎠⎟
⎟
⎝ ⎝
DD =
σA t
14

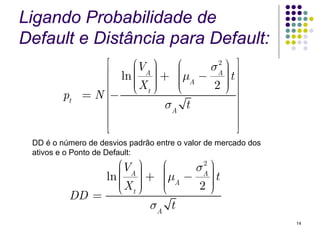
15. Ligando Probabilidade de
Default e Distância para Default:
pt = N [−DD ]
15

16. Obtendo probabilidades de
default reais a partir da DD
Assumindo que os ativos seguem um processo estocástico browninano
geométrico e homocedástico: p
t
= N [−DD ]
Uma curva empírica é
utilizada para corrigir os
efeitos do processo
estocástico assumido:
pt = EDF [−DD ]
16

17. Exemplo 1
Utilizando o mapeamento empírico: EDF = 25 bp (0,25%)
Utilizando o modelo normal: p= 2 bp (0.02%)
17

18. Exemplo 2
18

19. Comportamento do Ativo versus
Passivo em um Default Real
19

20. KMV e S&P em um Default Real
20

21. Bibliografia
•Crouhy M. Galai D. e Mark R., A comparative analysis of current credit risk
models, Journal of Banking and Finance 24 (2000) 59-117.
•Crosbie, P.J. e Bohn J., Modeling Default Risk, KMV, 2002
Leitura Complementar
Merton, R. On pricing of corporate debt: The risk structure of interest
rates. Journal of Finance 28, 449-470.
21