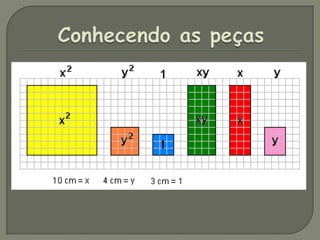
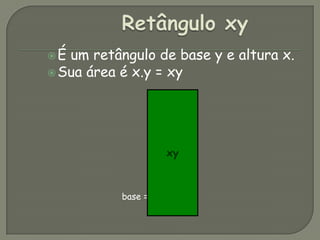
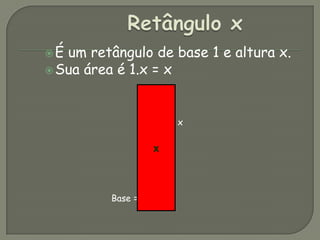
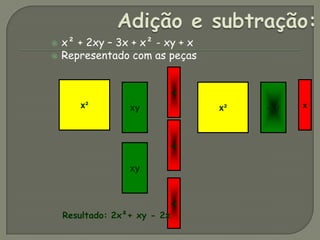
O documento descreve o método Algeplan, que usa figuras geométricas para ensinar álgebra. O método foi usado com 180 estudantes e mostrou-se efetivo para ensinar expressões algébricas, equações de primeiro e segundo grau e fatoração, motivando mais os alunos. O software Winplot também foi usado para explorar gráficos de funções quadráticas.

1. Algeplan Consiste em um método que relaciona figuras geométricas (quadrados e retângulos) com a álgebra

2. O objetivo deste trabalho é divulgar uma experiência (em sala de aula e laboratório de informática), onde certos conteúdos matemáticos foram trabalhados com o auxílio do material concreto Algeplan,

3. Expressões algébricas do primeiro e segundo graus, monômios e polinômios, resolução de equações do primeiro grau e fatoração de trinômios do segundo grau, são assuntos que, em geral, os alunos apresentam muita dificuldade na aprendizagem. Neste trabalho é apresentada a experiência realizada com alunos (180 alunos) do Ensino Fundamental (7as e 8as séries) e Médio (1ª e 2ª séries) com o material didático Algeplan

4. Conhecendo as peças

5. Quadrado x² É um quadrado de base x e altura x. Sua área é x . x = x² altura: x Base = x x²

6. Quadrado y² É um quadrado da base y e altura y. Sua área é y.y = y² altura = y base = y y²

7. Quadrado 1 É um quadrado de base 1 e altura 1. Sua área é 1.1 = 1 altura = 1 base = 1 1

8. Retângulo xy É um retângulo de base y e altura x. Sua área é x.y = xy altura= x base = y xy

9. Retângulo x É um retângulo de base 1 e altura x. Sua área é 1.x = x altura = x Base = 1 x

10. Retângulo y É um retângulo de base 1 e altura y. Sua área é 1.y = y altura = y base = y Y²

11. Adição e subtração: x² + 2xy – 3x + x² - xy + x Representado com as peças x² x² -x xy -xy x -x xy -x Resultado: 2x²+ xy - 2x

12. Utilizando software Integrando a Algeplan na informática, atraves do winplot

13. ATIVIDADES COM O WINPLOT : Usando o software “Winplot” pode-se explorar gráficos de funções quadráticas f(x) = ax2 + bx + c, com a, b, c reais e a ¹ 0, observando os zeros (quando existem - que correspondem às raízes da equação ax2+ bx + c = 0) e os valores máximo ou mínimo (obtidos no vértice). Indiretamente estudou-se também fatoração, pois, se f(x) é dada na forma“fatorada” f(x) = a(x - p)(x - q), ou seja, a(x - p)(x - q) é a fatoração do trinômio do 2º grau associado ax2 + bx + c, então obviamente os zeros da função são os elementos p e q.

14. Atividade . (Gráficos de funções quadráticas) Construa, usando o Winplot, o gráfico das funções listadas a seguir, observando os zeros/raízes (reais - quando existem) e os pontos de máximo ou mínimo/vértices. A partir do gráfico, obtenha se possível, a lei da função na forma fatorada, ou seja, obtenha a fatoração do trinômio do 2º grau associado a ax2 + bx + c. (Para o desenvolvimento dessa atividade é interessante que os exemplos propostos sejam tais que os zeros /raízes sejam números inteiros e não muito grandes).

15. Conclusão: Acreditamos que o resultado foi muito bom. Durante o desenvolvimento das atividades, observou-se que, com esse processo de aprendizagem, os alunos tornaram-se mais criativos e sentiram-se bem mais motivados. Na avaliação complementar feita no final das atividades pode-se constatar que a maioria dos alunos já estavam bem mais familiarizados com os conceitos envolvidos. Ressaltamos que esse tipo de atividade exigiu preparação anterior e, pelo menos mais uma pessoa (no caso as bolsistas) para colaborar em sala de aula com as professoras. Explorou-se a limitação do material, enfatizando que uma equação do 2º grau pode ter raízes reais não inteiras, ou mesmo, não ter raízes reais e, dependendo da série, pode-se falar na existência de raízes complexas.

16. LINKS DE TUTORIAS DO WINPLOT http://www.screencast.com/users/drummath/folders/Jing/media/5af3104f-42ff-44dd-a537-2b53390e4aeb http://www.screencast.com/users/drummath/folders/Default/media/ac285694-86fa-40c5-b29a-d20f48fb8971 http://www.screencast.com/users/drummath/folders/Jing/media/48c3f4d4-b7de-4fb3-9f50-c29b3fef09d4 http://www.screencast.com/users/drummath/folders/Jing/media/8c882ecb-c6cb-4d96-a8b9-8ecbab3f4395 http://www.screencast.com/users/drummath/folders/Jing/media/4fc19714-53b8-49eb-ad43-300120c71f2c http://www.screencast.com/users/drummath/folders/Jing/media/f7b3ebed-9bc5-4740-83c8-d1ebe190a36b