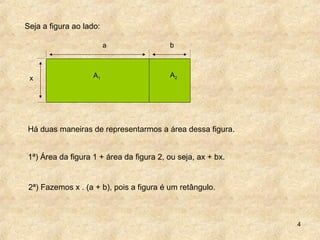
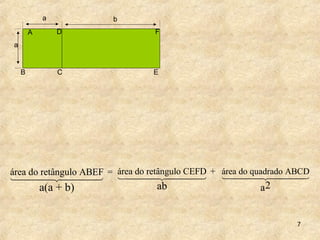
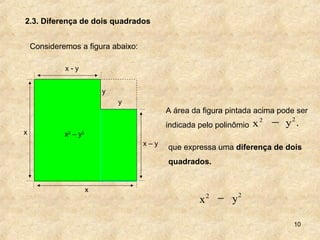
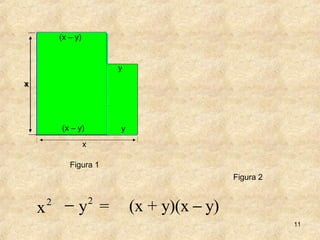
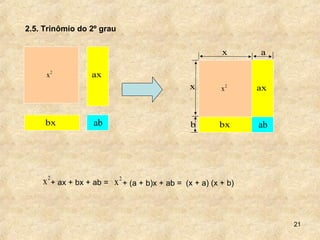
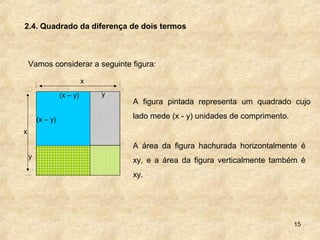
1. O documento discute técnicas de fatoração de expressões algébricas como polinômios, trinômios e diferenças de quadrados. 2. As técnicas incluem colocar fator comum em evidência, agrupamento de termos com fator comum e decompor trinômios perfeitos em produto de binômios. 3. A fatoração permite expressar expressões algébricas como produto de fatores, revelando sua estrutura.

1. 1
Uniban
Universidade Bandeirante de São Paulo
Fundamentos da Álgebra
Prof. Cícero
São Paulo – 2009

2. 2
CAPÍTULO III – Fatoração
1. Introdução
Consideremos o número 100.
Utilizando a multiplicação, podemos escrever esse número de várias maneiras:
100 =







2 . 50
4 . 25
5 . 20
2 2
2 . 5
10 . 10
Resumo detalhado sobre o assunto em:
http://www.algosobre.com.br/matematica/divisibilidade-e-a-decomposicao

3. 3
Quando escrevemos o número 100 na forma 2 . 50 ou 4 . 25 ou 5 . 20 ou 10 . 10,
transformamos esse número numa multiplicação de dois fatores.
numa multiplicação em que todos os fatores são números primos.
Quando escrevemos o número 100 na forma transformamos esse número2 2
2 . 5
Em qualquer um dos casos, fizemos a fatoração do número 100.
Como a palavra fatoração está associada a uma multiplicação, podemos dizer que:
Fatorar um número significa escrevê-lo como multiplicação de dois ou mais
fatores.

4. 4
a b
x A1
A2
Seja a figura ao lado:
Há duas maneiras de representarmos a área dessa figura.
1ª) Área da figura 1 + área da figura 2, ou seja, ax + bx.
2ª) Fazemos x . (a + b), pois a figura é um retângulo.

5. 5
Quando escrevermos o polinômio ax + bx na forma x (a + b), estamos
transformando o polinômio inicial numa multiplicação de polinômios,
Portanto, fatorar um polinômio, quando for possível, significa escrever esse
polinômio com uma multiplicação de dois ou mais polinômios.
Daí podemos escrever:
polinômio
ax + bx =14243
multiplicação de
polinômios
x (a + b)
14243

6. 6
2. Técnicas de fatoração
2.1. Colocação de um fator comum em evidência
A figura abaixo mostra um quadrado ABCD, um retângulo CEFD e um retângulo
ABEF.
a b
A
C EB
D F
a
De acordo com a figura, podemos escrever:

7. 7
área do quadrado ABCD
2a
14444244443
a b
A
C EB
D F
a
área do retângulo CEFD +
ab
14444244443área do retângulo ABEF =
a(a + b)
14444244443

8. 8
2.1. Agrupamento
Observe as 3 figuras seguintes:
ba
x
y
a b
x
y
ax
ay
bx
by
ba
x
y
x.(a + b)
y.(a + b)
A área dessa figura
pode ser dada pelo
polinômio
ax + bx + ay + by.
A área dessa figura
pode ser dada pelo
polinômio
x(a + b) + y(a + b).
A área dessa figura
pode ser dada pelo
polinômio
(a + b) (x + y).

9. 9
Como as três figuras têm a mesma área, podemos escrever:
polinômio
ax + bx + ay + by =
144424443 x . (a + b) + y . (a + b) =
forma fatorada
do polinômio
(a + b) (x + y)
1442443
Vejamos como podemos fazer algebricamente para escrever o polinômio
ax + bx + ay + by na forma fatorada:
ax + bx + ay + by14243 14243 Agrupamos os termos que possuem fator comum
x (a + b) + y (a + b) Em cada grupo colocamos os fatores comuns em
evidência
(a + b) (x + y) Colocamos, novamente, em evidência o fator comum

10. 10
2.3. Diferença de dois quadrados
Consideremos a figura abaixo:
x - y
y
y
x
x
x2
– y2
x – y
que expressa uma diferença de dois
quadrados.
2
x
2
y−
A área da figura pintada acima pode ser
indicada pelo polinômio
2
x
2
y .−

11. 11
y
(x – y)
(x – y)
(x – y)
x
y
y
(x – y)
x
(x – y)
x
(x + y)(x y)−2
x
2
y =−
Figura 1
Figura 2

12. 12
Recortando a figura (ver fig. 1) pelo tracejado formamos uma nova figura (ver fig. 2)
quando juntamos as duas partes:
A área da figura 2 é expressa por (x + y) (x – y).
Como as áreas são iguais, logo podemos escrever:
(x + y)(x y)−2
x
2
y =−
A área da figura 1 é expressa por
2 2
x y .−

13. 13
Na forma fatorada, podemos observar que:
2
x = x raiz quadrada do 1º termo do polinômio
2
y = y raiz quadrada do 2º termo do polinômio
Então:
2 2
x - y =
2 2x x2 2y y
( x + y) ( x + y)
↓ ↓↓ ↓

14. 14
2.4. Quadrado da soma de dois termos
Vamos considerar a seguinte figura:
x2
y2xy
xyx
x
y
y
A figura representa um quadrado cujo lado
mede (x + y) unidades de comprimento.
A área da figura pode ser indicada de duas
maneiras:
2 2
x + 2xy + y ou
2
(x + y)

15. 15
2.4. Quadrado da diferença de dois termos
Vamos considerar a seguinte figura:
A figura pintada representa um quadrado cujo
lado mede (x - y) unidades de comprimento.
A área da figura hachurada horizontalmente é
xy, e a área da figura verticalmente também é
xy.
x
y
(x – y)
(x – y)
x
y

16. 16
e é comum a outras duas áreas hachuradas. A
área da figura pintada é:
2 2
x 2xy + y− ou
2
(x y)−
x
y
(x – y)
(x – y)
x
y
A área da figura com hachura quadriculada é
2
y

17. 17
Então, podemos escrever as seguintes igualdades:
2 2 2
polinômio forma fatorada
do polinômio
x + 2xy + y = (x + y) (x + y) = (x + y)
1442443 14243
2 2 2
polinômio forma fatorada
do polinômio
x - 2xy + y = (x - y) (x - y) = (x - y)
1442443 123

18. 18
Trinômios porque possuem três termos, quadrados perfeitos porque o primeiro
representa o quadrado de (x + y), enquanto o segundo representa o quadrado
de (x – y).
Os polinômios e são chamados trinômios
quadrados perfeitos.
2 2
x + 2xy + y 2 2
x 2xy + y−

19. 19
A seguir, determinamos a raiz quadrada de cada termo quadrado:
2
x x= 4y16y2
=e
Finalmente, multiplicamos por 2 o produto das raízes para verificar se o resultado
é igual ao termo restante: 2 . x . 4y = 8xy
Exemplo 1: Fatore + 8xy +
2
x 2
16y .
Inicialmente, verificamos se dois termos do trinômio são quadrados. Neste
caso, e são quadrados.
2
x 2
16y

20. 20
Como, neste caso, o termo é justamente 8xy, dizemos que o trinômio é
quadrado perfeito.
Então sua forma fatorada é:
4x16x2
= 525 =e
2 . 4x . 5 = 40x , não corresponde ao termo restante do trinômio.
+ 8xy + 16 =
2
x 2
y 2
(x + 4y)
Exemplo 2: Fatore 16 – 24x + 25.2
x
e 25 são termos quadrados.
2
16x
Logo, – 24x + 25 não é um trinômio quadrado perfeito.
2
16x

21. 21
ab
ax
bx
2
x
ax
b
x
2.5. Trinômio do 2º grau
ab
ax
bx
2
x
2
x + ax + bx + ab =
2
x + (a + b)x + ab = (x + a) (x + b)

22. 22
pode ser decomposto num produto de dois binômios do 1º grau da seguinte
maneira:
Um trinômio do 2º grau da forma + Sx + P, em que S = a + b e P = p . q,
2
x
+ Sx + P = (x + a)(x + b), sendo S = a + b e P = a . b
2
x