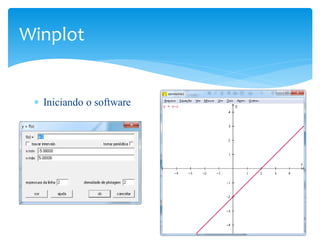
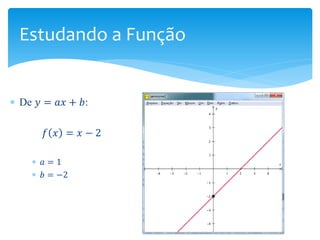
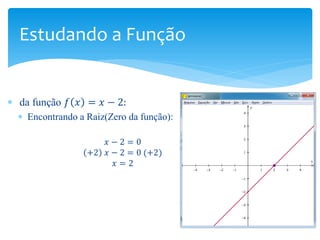
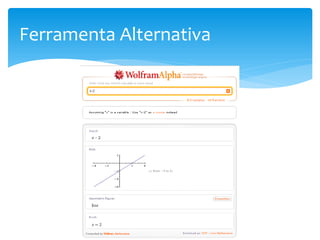
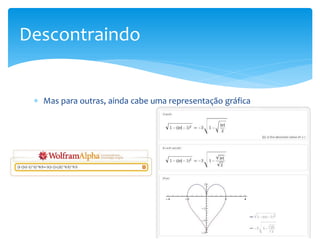
O documento discute o software Winplot, que permite plotar gráficos de funções matemáticas. Apresenta brevemente a história do software, suas características, comandos básicos e como pode ser útil no ensino de funções para estudantes de graduação. Uma ferramenta alternativa é o Wolfram Alpha, que tem funcionalidades semelhantes.

1. Estudo de Funções com o
Software Winplot
RODRIGO ROMAIS
Departamento de Matemática – UNEMAT/Sinop
r.romais@gmail.com

2. “A utilização e elegância da matemática
reside na sua capacidade de explorar as
ligações formais entre problemas
aparentemente distintos” - Richard Parris

3. Breve Histórico
∗ Criado por Richard Parris em 1985;
∗ Chamava-se Plot, utilizado no sistema operacional DOS
(Sistema Operacional em Disco);
∗ Com o surgimento do Windows 3.1, o programa é
rebatizado para Winplot.

4. Winplot
∗ Características do Winplot:
∗ Software grátis;
∗ Código fonte aberto (Programado em C++);
∗ Executável (não necessita ser instalado);
∗ Pequeno e Portável (tamanho: 1,75Mb);
∗ Versão em língua portuguesa;
∗ Depende de linguagem básica de programação;
∗ Exibe gráficos em 2D e 3D.

5. Winplot
∗ Sobre:

6. Winplot
∗ Iniciando o software

7. Winplot
∗ Iniciando o software

8. Winplot
∗ Iniciando o software

9. Estudando a Função
∗ A equação geral de uma reta é:
𝑦 = 𝑎𝑎 + 𝑏
𝑎 – é o coeficiente angular da reta;
𝑏 – constante da função;
∗
𝑥 – Variável Independente;
∗
𝑦 – Variável Dependente.
∗
∗

10. Estudando a Função
∗ De 𝑦 = 𝑎𝑎 + 𝑏:
𝑓 𝑥 = 𝑥−2
∗ 𝑎=1
∗ 𝑏 = −2

11. Estudando a Função
∗ da função 𝑓 𝑥 = 𝑥 − 2:
∗ Encontrando a Raiz(Zero da função):
𝑥−2=0
+2 𝑥 − 2 = 0 (+2)
𝑥=2

12. Comandos Básicos do Winplot
∗ a+b = adição entre os valores de a e b
∗ a-b = subtração entre os valores de a e b
∗ a*b = ab = multiplicação entre os valores de a e b ∗ sin(x) = seno de x
∗ a/b = divisão entre os valores de a e b ∗ cos(x) = cosseno de x
∗ a^b = a elevado a potência b ∗ tan(x) = tangente de x
∗ csc(x) = cossecante de x
∗ pi = 3,141592654 ∗ sec(x) = secante de x
∗ e = 2,718281828 ∗ cot(x) = cotangente de x
∗ sqrt(x) = raiz quadrada de x ∗ n! = n fatorial
∗ log(x) = logaritmo de x na base 10
∗ log(b,x) = ln(x)/ln(b) logaritmo de x na base b
∗ ln(x) = logaritmo natural de x
∗ exp(x) = exponencial de x

13. Ferramenta de Ensino
∗ Como o software Winplot pode ser útil no ensino da
matemática?
∗ Como o Winplot pode auxiliar nas dificuldades sobre
funções dos acadêmicos?

14. Ferramenta de Ensino
∗ O Winplot é uma ferramenta que plota funções, isto é,
mostra graficamente o comportamento de uma função.
∗ Entendendo a dificuldade dos alunos dos semestres
iniciais da graduação, quanto ao conceito básico de
funções, o software dá esse apoio visual de uma função,
facilitando a compreensão matemática.

15. Ferramenta Alternativa
∗ Uma ferramenta alternativa ao Winplot, é o Wolfram
Alpha, um site que tem função bem semelhante.
http://www.wolframalpha.com/

16. Ferramenta Alternativa

17. Ferramenta Alternativa

18. Descontraindo
∗ Algumas coisas nem sempre podem ser explicadas através da
matemática, como algumas sensações, nas quais não podem ser
quantificadas, já outras são imensuráveis.

19. Descontraindo
∗ Mas para outras, ainda cabe uma representação gráfica

20. Referências Bibliográficas
∗ ROMAIS, Rodrigo. “Apostila: Minicurso Scilab versão
4.1.2. 4º Encontro Estadual de Ensino de Matemática,
Sinop-MT. 2008”.
∗ http://www.mat.ufpb.br/sergio/winplot/winplot.html
∗ http://www.gregosetroianos.mat.br/softwinplot.asp