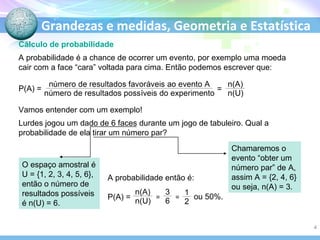
1) O documento discute experimentos aleatórios, espaço amostral e cálculo de probabilidade usando exemplos de jogos de tabuleiro com dados. 2) Um espaço amostral representa todos os resultados possíveis de um experimento aleatório, como os números de 1 a 6 para um dado regular. 3) A probabilidade é a chance de um evento ocorrer, como tirar um número par em um dado, e é calculada dividindo o número de resultados favoráveis pelo total de resultados possíveis.

1. Grandezas e medidas, Geometria e Estatística
Experimento aleatório e espaço amostral
Em 7 jogadas diferentes, Lucas obteve os seguintes valores:
Durante um jogo de tabuleiro, Bruna e Lucas jogam um dado de seis lados.
Probabilidade
MAUROSOUZA/ARQUIVODAEDITORA
1

2. Grandezas e medidas, Geometria e Estatística
Se em condições idênticas jogarmos um dado repetidas vezes podemos prever
qual face cairá voltada para cima?
Os resultados são imprevisíveis e por isso denominamos o lançamento de um
dado um experimento aleatório.
Não!
Retomando o exemplo do jogo de tabuleiro, para cada jogada do dado, os
resultados possíveis são: 1, 2, 3, 4, 5 e 6.
Esses valores correspondem ao espaço amostral que representamos
por U (de “Universo”).
Assim, no exemplo o espaço amostral é U = {1, 2, 3, 4, 5, 6}.
2

3. Grandezas e medidas, Geometria e Estatística
Evento
Então, o evento “sair um número maior que cinco” pode ser representado
por A = {5, 6} .
O jogo de Bruna e Lucas estava chegando ao fim e Bruna precisava tirar
um número maior ou igual a cinco para ganhar.
Ou seja, Bruna precisava tirar 5 ou 6!
Esse conjunto de valores que podem dar
vitória a Bruna é um subconjunto do
espaço amostral U = {1, 2, 3, 4, 5, 6}.
Esse subconjunto é denominado evento e
geralmente é representado por uma letra
maiúscula (A, B, C, ...).
MAUROSOUZA/ARQUIVODAEDITORA
3

4. Grandezas e medidas, Geometria e Estatística
Cálculo de probabilidade
A probabilidade é a chance de ocorrer um evento, por exemplo uma moeda
cair com a face “cara” voltada para cima. Então podemos escrever que:
P(A) =
Vamos entender com um exemplo!
Lurdes jogou um dado de 6 faces durante um jogo de tabuleiro. Qual a
probabilidade de ela tirar um número par?
Chamaremos o
evento “obter um
número par” de A,
assim A = {2, 4, 6}
ou seja, n(A) = 3.
O espaço amostral é
U = {1, 2, 3, 4, 5, 6},
então o número de
resultados possíveis
é n(U) = 6.
=
A probabilidade então é:
P(A) = ou 50%.= =
4

5. Grandezas e medidas, Geometria e Estatística
Evento impossível e evento certo
O professor Paulo vai sortear um livro de aventuras entre seus 30 alunos. Para
isso ele escreveu em pedaços de papel os números de 1 a 30.
Qual a probabilidade de ele sortear um número maior que 40?
O número de resultados favoráveis é zero, pois não há no espaço amostral
nenhum número maior do que 30!
Denominando o evento
como A temos que n(A) = 0.
Como o espaço amostral é
composto de papéis com
números de 1 a 30, n(U) = 30.
Logo, a probabilidade é: P(A) = P(A) = 0
Portanto a probabilidade de o professor sortear um número maior que 40 é
zero, ou seja, nunca ocorrerá!
Eventos que nunca ocorrerão são chamados de eventos impossíveis.
=
5

6. Grandezas e medidas, Geometria e Estatística
Agora, vamos calcular a probabilidade de o professor sortear um número
menor ou igual a 30?
O número de resultados favoráveis é 30, pois entre os números de 1 a 30
há 30 números que são menores ou iguais a 30. O espaço amostral
continua o mesmo.
Denominando o evento como
B temos que n(B) = 30.
Como o espaço amostral é
composto de papéis com
números de 1 a 30, n(U) = 30.
Logo, a probabilidade é: P(B) = P(B) = 1 ou 100%
Portanto a probabilidade de o professor sortear um número menor ou igual a
30 é 1, ou seja, sempre ocorrerá!
Eventos que sempre ocorrerão são chamados de eventos certos.
=
6

7. Grandezas e medidas, Geometria e Estatística
Eventos equiprováveis e eventos não equiprováveis
Ou seja, os eventos têm a mesma probabilidade e os chamamos de eventos
equiprováveis.
Imagine agora um dado que não possui uma face com o
número 1 e possui duas faces com o número 6.
Qual a probabilidade de sair a face com o número 1
voltada para cima?
E com o número 4?
E com o número 6?
P(A) = 0
Esse evento é
impossível!
Esses eventos não têm a mesma
probabilidade, então os chamamos
de eventos não equiprováveis.
3
6 2 5 6
4
P(B) =
P(C) = =
Ao lançar um dado de seis faces a probabilidade de cada face sair é .
7